Cross-Validation vs. Bootstrapping: A Practical Guide for Biomedical Researchers

Noah Brooks Dec 02, 2025 199

This article provides a comprehensive comparison of cross-validation and bootstrapping for researchers, scientists, and professionals in drug development.

Cross-Validation vs. Bootstrapping: A Practical Guide for Biomedical Researchers

Abstract

This article provides a comprehensive comparison of cross-validation and bootstrapping for researchers, scientists, and professionals in drug development. It covers the foundational principles of both internal validation techniques, their methodological applications in clinical prediction models, and practical strategies for troubleshooting and optimization with real-world biomedical data. A detailed, evidence-based comparative analysis guides the selection of the appropriate technique based on dataset size, outcome characteristics, and modeling goals, with a focus on enhancing the reliability and generalizability of predictive models in healthcare.

Core Concepts: Understanding Internal Validation and the Problem of Optimism

The Critical Need for Internal Validation in Clinical Prediction Models

The development of clinical prediction models (CPMs) has seen exponential growth across all medical fields, with an estimated nearly 250,000 articles reporting the development of CPMs published to date [1]. This proliferation underscores the critical role predictive analytics plays in modern healthcare, from prognosis in oncology to estimating osteopenia risk. However, this abundance also highlights concerns about research waste and the limited application of many models in clinical practice. The chasm between development and implementation exists largely because the generalizability of predictive algorithms often goes untested, leaving the community in the dark regarding their real-world accuracy and safety [2].

Internal validation serves as the essential first step in addressing this challenge, providing optimism-corrected estimates of model performance within the development dataset. Without rigorous internal validation, researchers cannot determine whether their model has learned robust statistical relationships or has simply memorized noise in the training data—a phenomenon known as overfitting. This article provides a comprehensive comparison of the two predominant internal validation methodologies—cross-validation and bootstrapping—examining their theoretical foundations, experimental performance, and optimal applications in clinical prediction research.

Internal Validation Fundamentals: Cross-Validation vs. Bootstrapping

Methodological Frameworks

Internal validation aims to assess the reproducibility of algorithm performance in data distinct from the development data but derived from the same underlying population [2]. Cross-validation and bootstrapping represent the two most recommended approaches for this purpose, each with distinct mechanistic philosophies.

Cross-validation operates on a data-splitting principle. The most common implementation, k-fold cross-validation, partitions the dataset into k equal parts (typically 5 or 10). The model is trained on k-1 folds and validated on the remaining holdout fold. This process rotates until each fold has served as the validation set, with performance metrics averaged across all iterations [3] [2]. Nested cross-validation extends this approach by incorporating an outer loop for performance estimation and an inner loop for hyperparameter tuning, further reducing optimism bias [3].

Bootstrapping employs a resampling-based strategy, drawing multiple random samples from the original dataset with replacement (typically 500-2000 iterations) [2]. Each bootstrap sample is used to train a model, with performance evaluated on the out-of-bag (OOB) observations not included in the resample [4]. Several variants exist, including the optimism bootstrap (Efron-Gong method), the .632 bootstrap which adjusts for the bias that approximately 63.2% of unique observations are represented in each bootstrap sample, and the .632+ bootstrap which further corrects for situations with high overfitting [5].

Comparative Workflows

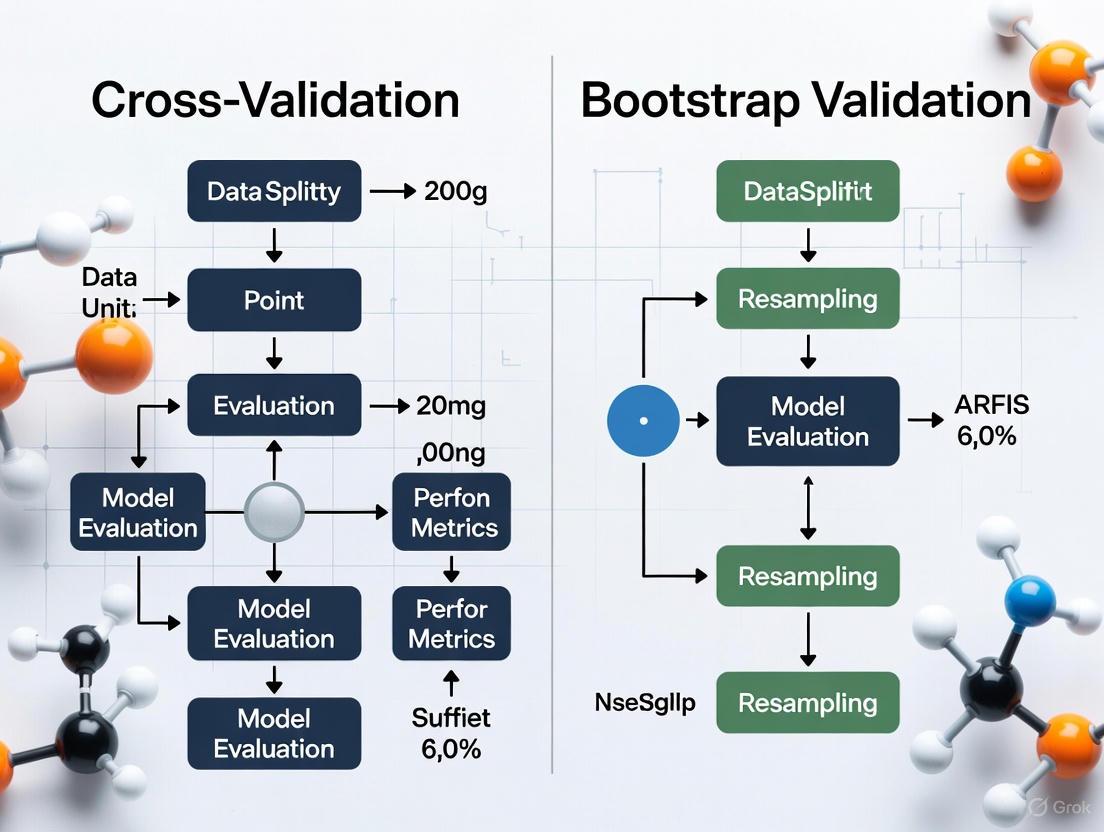
The fundamental differences between these methodologies can be visualized through their operational workflows:

G cluster_cv Cross-Validation Workflow cluster_boot Bootstrap Workflow CVStart 1. Original Dataset CVSplit 2. Split into K Folds CVStart->CVSplit CVTrain 3. Train on K-1 Folds CVSplit->CVTrain CVTest 4. Validate on Held-Out Fold CVTrain->CVTest CVRepeat 5. Repeat K Times CVTest->CVRepeat CVRepeat->CVTrain Rotate holdout fold CVAggregate 6. Aggregate Performance Metrics CVRepeat->CVAggregate BootStart 1. Original Dataset BootResample 2. Resample with Replacement BootStart->BootResample BootTrain 3. Train on Bootstrap Sample BootResample->BootTrain BootTest 4. Validate on Out-of-Bag Data BootTrain->BootTest BootRepeat 5. Repeat B Times (100-2000) BootTest->BootRepeat BootRepeat->BootResample New resample BootAggregate 6. Aggregate Performance Metrics BootRepeat->BootAggregate

Experimental Performance Comparison

Quantitative Findings from Simulation Studies

Recent benchmark studies have provided empirical evidence comparing these validation strategies. A comprehensive simulation study focused on high-dimensional prognosis models using transcriptomic data from head and neck tumors offers particularly insightful results [5] [6] [7]. The study evaluated performance across multiple sample sizes (n=50 to n=1000) using time-dependent AUC and integrated Brier Score as metrics.

Table 1: Performance Comparison Across Internal Validation Methods

Validation Method Sample Size Discrimination Calibration Overall Stability
Train-Test Split All sizes Unstable Unstable Poor
Conventional Bootstrap n=50-100 Over-optimistic Moderate Moderate
0.632+ Bootstrap n=50-100 Overly pessimistic Moderate Moderate
K-Fold Cross-Validation n=50-100 Moderate Moderate Good
K-Fold Cross-Validation n=500-1000 Good Good Excellent
Nested Cross-Validation n=50-100 Good (varies) Good (varies) Moderate
Nested Cross-Validation n=500-1000 Excellent Excellent Good

The findings demonstrate that k-fold cross-validation and nested cross-validation showed improved performance with larger sample sizes, with k-fold cross-validation demonstrating greater stability [6]. Conventional bootstrap methods tended to be over-optimistic in their performance estimates, while the 0.632+ bootstrap correction could swing to overly pessimistic, particularly with small samples (n=50 to n=100) [5] [6].

Context-Dependent Recommendations

The optimal choice between cross-validation and bootstrapping depends on specific research contexts:

  • Small sample sizes (n < 200): Bootstrapping is often preferred due to its stability and utility for uncertainty estimation [8], though the 0.632+ variant may require careful interpretation of potentially pessimistic bias [5].

  • High-dimensional data (e.g., genomics, transcriptomics): K-fold cross-validation is recommended as bootstrapping can overfit due to repeated sampling of the same individuals [5] [8] [6].

  • Time-to-event endpoints: K-fold and nested cross-validation show superior performance for Cox penalized models [5] [6].

  • Computational constraints: Repeated k-fold cross-validation requires 50-100 repetitions for sufficient precision, making bootstrap (with 300-1000 repetitions) sometimes faster [4].

Implementation Protocols

Cross-Validation Protocol

For researchers implementing k-fold cross-validation, the following detailed protocol is recommended:

  • Data Preparation: Handle missing data, outliers, and ensure appropriate feature scaling. For clinical data with repeated measures, implement subject-wise splitting to prevent data leakage [3].

  • Stratification: For classification problems with imbalanced outcomes, use stratified cross-validation to maintain consistent outcome rates across folds [3].

  • Fold Selection: Choose an appropriate k-value based on sample size. The common choices are 5-fold or 10-fold cross-validation [2].

  • Model Training: For each training fold, include hyperparameter tuning if needed. For nested cross-validation, this occurs in an inner loop [3].

  • Performance Aggregation: Calculate performance metrics (discrimination, calibration) for each test fold and aggregate using appropriate averaging methods [3].

  • Stability Enhancement: Repeat the entire k-fold procedure multiple times (e.g., 10×10-fold cross-validation) for more stable estimates [2].

Bootstrap Validation Protocol

For bootstrap validation implementations:

  • Resampling Scheme: Generate B bootstrap samples (typically 100-2000) by sampling with replacement from the original dataset [2].

  • Model Training: Train a model on each bootstrap sample [4].

  • Out-of-Bag Testing: Evaluate performance on the observations not selected in each bootstrap sample (approximately 36.8% of the original data) [4].

  • Optimism Calculation: For the optimism bootstrap, calculate the difference between bootstrap performance and performance on the original dataset [4].

  • Bias Correction: Apply appropriate corrections (.632 or .632+) based on the degree of overfitting [5].

  • Performance Estimation: Derive the final optimism-corrected performance estimate [4].

The Scientist's Toolkit: Research Reagent Solutions

Table 2: Essential Resources for Internal Validation Research

Resource Category Specific Tools Function in Validation
Statistical Computing R Software (version 4.4.0) [5] Primary platform for implementing validation algorithms and analysis
Simulation Frameworks Custom R scripts [6] Generate synthetic datasets with known properties for method validation
High-Performance Computing Parallel processing clusters [3] Handle computational demands of repeated resampling (100-2000 iterations)
Data Repositories MIMIC-III [3], SCANDARE [5] Provide real-world clinical datasets for validation experiments
Specialized Algorithms Cox Penalized Regression [5] [6] Reference models for high-dimensional time-to-event data validation
Performance Metrics Time-dependent AUC, C-index, Integrated Brier Score [5] Quantify discrimination and calibration for time-to-event outcomes

The critical need for internal validation in clinical prediction models cannot be overstated. As the proliferation of new models continues, rigorous validation becomes increasingly essential to distinguish truly predictive algorithms from those that merely fit noise. The experimental evidence demonstrates that both cross-validation and bootstrapping offer distinct advantages, with k-fold cross-validation generally providing more stable performance estimates, particularly in high-dimensional settings, while bootstrap methods offer valuable insights into uncertainty.

Researchers must select their validation strategy based on their specific context—considering sample size, data dimensionality, outcome type, and computational resources. Regardless of the method chosen, comprehensive internal validation represents the essential foundation upon which clinically useful prediction models are built, serving as the critical bridge between development and meaningful clinical implementation.

In machine learning, overfitting occurs when a model fits too closely or even exactly to its training data, learning the "noise" or irrelevant information within the dataset, rather than the underlying pattern [9]. This creates a dangerous illusion: a model that appears to perform exceptionally during training but fails to generalize to new, unseen data [9]. For researchers and scientists in critical fields like drug development, this deception can have serious consequences, leading to incorrect conclusions based on models that will not hold up in real-world validation. The core of the problem lies in the model's inability to establish the dominant trend within the data, instead memorizing the training set [9]. This article, framed within a broader thesis on validation techniques, will objectively compare two fundamental methods for detecting and preventing this issue: cross-validation and bootstrap validation.

Unmasking the Deception: What is Overfitting?

A model is considered overfitted when it demonstrates low error rates on its training data but high error rates on test data it has never seen before [9]. This signals that the model has mastered the training data but cannot apply its "knowledge" broadly. The opposite problem, underfitting, occurs when a model has not trained for enough time or lacks sufficient complexity to capture the meaningful relationships in the data [9]. The goal of any model fitting process is to find the "sweet spot" between these two extremes, creating a model that generalizes well [9].

Quantifying this phenomenon is an active area of research. Recent work has introduced the Overfitting Index (OI), a novel metric designed to quantitatively assess a model's tendency to overfit, providing an objective lens to gauge this risk [10].

The Scientist's Toolkit: Cross-Validation vs. Bootstrap Validation

To combat overfitting, researchers rely on robust validation techniques. The following table details the key "research reagents" – the methodological solutions – essential for this task.

Research Reagent / Method Primary Function Key Advantages
K-Fold Cross-Validation [11] Partitions data into 'k' subsets for iterative training and validation. Provides a good bias-variance tradeoff; excellent for model selection and hyperparameter tuning [11].
Stratified K-Fold [11] A variant that preserves the target variable's distribution in each fold. Crucial for imbalanced datasets, ensuring representative folds [11].
Leave-One-Out Cross-Validation (LOOCV) [11] Uses a single observation as the test set and the rest for training. Provides an almost unbiased estimate but is computationally expensive [11].
Bootstrap Validation [11] Creates multiple training sets by sampling data with replacement. Effective for small datasets and provides an estimate of performance metric variability [11].
Out-of-Bag (OOB) Error [11] Uses data points not selected in a bootstrap sample for validation. Provides a built-in validation mechanism without a separate holdout set [4].
Early Stopping [9] Halts the training process before the model begins to learn noise. A simple yet effective regularization technique to prevent overtraining.
Regularization (e.g., Dropout) [12] Applies penalties to model parameters or randomly drops neurons during training. Reduces model complexity and dependency on specific neurons, combating overfitting [9] [12].

Methodological Deep Dive: Core Protocols

Cross-Validation Protocol

The standard k-fold cross-validation methodology involves several key steps [11]:

  • Data Partitioning: Randomly shuffle the dataset and split it into k mutually exclusive folds of approximately equal size.
  • Iterative Training and Validation: For each of the k iterations:
    • Designate one fold as the validation (test) set.
    • Combine the remaining k-1 folds to form the training set.
    • Train the model on the training set.
    • Evaluate the model on the validation set and record the performance score (e.g., accuracy, R²).
  • Performance Aggregation: Calculate the final model performance estimate by averaging the scores from all k iterations.

The following diagram illustrates this workflow:

CV Start Start: Dataset Shuffle Shuffle Dataset Start->Shuffle Split Split into k Folds Shuffle->Split Loop For each of k iterations Split->Loop TrainSet Form Train Set (k-1 Folds) Loop->TrainSet ValSet Form Validation Set (1 Fold) Loop->ValSet Train Train Model TrainSet->Train Validate Validate Model Train->Validate Score Record Performance Score Validate->Score Decision All iterations complete? Score->Decision Decision->Loop No Result Final Score = Average of k scores Decision->Result Yes

Bootstrap Validation Protocol

The bootstrap methodology follows a distinct resampling approach [11] [4]:

  • Bootstrap Sample Generation: For B iterations (typically 1000 or more), draw a random sample of size n from the original dataset with replacement. This is a single bootstrap sample.
  • Model Training and OOB Evaluation:
    • Train the model on the bootstrap sample.
    • Use the out-of-bag (OOB) data—the data points not included in the bootstrap sample—as a validation set.
    • Evaluate the model on the OOB data and record the performance score.
  • Result Aggregation: Average the results from all B bootstrap iterations to produce an overall performance estimate. The variability of these scores also provides an estimate of the model's stability.

The workflow for bootstrap validation is captured in the diagram below:

Bootstrap Start Start: Dataset (n samples) Loop For B iterations (e.g., 1000) Start->Loop Sample Draw Bootstrap Sample (n samples with replacement) Loop->Sample IdentifyOOB Identify Out-of-Bag (OOB) Data Sample->IdentifyOOB Train Train Model on Bootstrap Sample IdentifyOOB->Train Validate Validate Model on OOB Data Train->Validate Score Record OOB Performance Score Validate->Score Decision All iterations complete? Score->Decision Decision->Loop No Result Final Score = Average of B OOB scores Decision->Result Yes

Comparative Analysis: Experimental Data and Performance

The choice between cross-validation and bootstrapping is not one-size-fits-all. It depends on the dataset size, the model's characteristics, and the goal of the validation. The table below summarizes experimental insights from comparative studies.

Aspect Cross-Validation Bootstrap Validation
Data Partitioning Splits data into mutually exclusive 'k' folds [11]. Samples data with replacement to create multiple bootstrap datasets [11].
Bias & Variance Tends to have lower variance but may have higher bias with small 'k' [11]. Can provide a lower bias estimate but may have higher variance due to resampling [11] [4].
Ideal Use Cases Model comparison, hyperparameter tuning, and with large, balanced datasets [11]. Small datasets, variance estimation, and scenarios with significant data noise or uncertainty [11].
Computational Load Computationally intensive for large 'k' or large datasets [11]. Also computationally demanding, especially for a large number of bootstrap samples (B) [11].
Performance Findings Repeated 5 or 10-fold CV is often recommended for a good balance [4]. The .632+ bootstrap method is effective, particularly for smaller samples [4]. Out-of-bag bootstrap error rates tend to have less uncertainty/variance than k-fold CV, but may have a bias similar to 2-fold CV [4].

For the researcher in drug development, where predictive accuracy is paramount, understanding the deceptive nature of apparent performance is non-negotiable. Overfitting poses a persistent threat that can only be countered by rigorous validation practices. Both k-fold cross-validation and bootstrap validation are powerful, essential tools in the modern scientist's arsenal. Cross-validation, particularly repeated 5 or 10-fold, offers a robust and widely trusted standard for model selection and tuning in many scenarios. In contrast, bootstrap methods, especially the .632+ variant, provide a critical alternative for smaller datasets or when an estimate of performance variability is needed. The ongoing research into metrics like the Overfitting Index [10] and the nuanced "double descent" risk curve [9] highlights that the field continues to evolve. Ultimately, the informed application of these validation protocols is our best defense against the siren song of a model that looks too good to be true.

Cross-validation is a fundamental statistical technique used to evaluate the performance and generalizability of predictive models. In an era where machine learning and artificial intelligence are increasingly applied to critical domains such as drug development and biomedical research, proper model validation has become paramount. Cross-validation addresses a crucial challenge in predictive modeling: the need to assess how well a model trained on available data will perform on unseen future data. This assessment helps prevent overoptimistic expectations that can arise when models are evaluated on the same data used for training, a phenomenon known as overfitting [13].

The core principle of cross-validation involves systematically partitioning a dataset into complementary subsets, performing model training on one subset (training set), and validating the model on the other subset (validation or test set). This process is repeated multiple times with different partitions, and the results are aggregated to produce a more robust performance estimate. Unlike single holdout validation, which uses a one-time split of the data, cross-validation maximizes data utility by allowing each data point to be used for both training and validation across different iterations [14] [3].

Within the broader context of validation methodologies, cross-validation serves as a cornerstone technique alongside resampling methods like bootstrap validation. While bootstrap validation involves drawing repeated random samples with replacement from the original dataset, cross-validation employs structured partitioning without replacement. This tutorial focuses specifically on two prominent cross-validation approaches—k-fold and leave-one-out cross-validation—comparing their methodological foundations, statistical properties, and practical applications in scientific research and drug development.

Understanding k-Fold Cross-Validation

Conceptual Foundation and Workflow

K-fold cross-validation is one of the most widely used cross-validation techniques in machine learning and statistical modeling. In this approach, the dataset is randomly partitioned into k approximately equal-sized subsets or "folds." The model training and validation process is then repeated k times, with each fold serving exactly once as the validation set while the remaining k-1 folds are used for training [15] [14]. This systematic rotation through all folds ensures that every observation in the dataset is used for both training and validation, just in different iterations.

The k-fold cross-validation process follows a specific workflow. First, the entire dataset is shuffled and divided into k folds of roughly equal size. For each iteration (from 1 to k), one fold is designated as the test set, and the remaining k-1 folds form the training set. A model is trained on the training set and its performance is evaluated on the test set. The performance metrics (e.g., accuracy, mean squared error) from all k iterations are then averaged to produce a single estimation of model performance [14]. This averaged result represents the cross-validation estimate of how the model is expected to perform on unseen data.

kfold Dataset Dataset Fold1 Fold 1 Dataset->Fold1 Fold2 Fold 2 Dataset->Fold2 Fold3 Fold 3 Dataset->Fold3 Fold4 Fold 4 Dataset->Fold4 Fold5 Fold 5 Dataset->Fold5 Iteration2 Iteration 2: Folds 1,3-5 Train Fold 2 Test Fold1->Iteration2 Fold1->Iteration2 Iteration3 Iteration 3: Folds 1-2,4-5 Train Fold 3 Test Fold1->Iteration3 Iteration4 Iteration 4: Folds 1-3,5 Train Fold 4 Test Fold1->Iteration4 Iteration5 Iteration 5: Folds 1-4 Train Fold 5 Test Fold1->Iteration5 Iteration1 Iteration 1: Folds 2-5 Train Fold 1 Test Fold2->Iteration1 Fold2->Iteration3 Fold2->Iteration3 Fold2->Iteration4 Fold2->Iteration5 Fold3->Iteration1 Fold3->Iteration2 Fold3->Iteration4 Fold3->Iteration4 Fold3->Iteration5 Fold4->Iteration1 Fold4->Iteration2 Fold4->Iteration3 Fold4->Iteration5 Fold4->Iteration5 Fold5->Iteration1 Fold5->Iteration1 Fold5->Iteration2 Fold5->Iteration3 Fold5->Iteration4 Results Average Results Iteration1->Results Iteration2->Results Iteration3->Results Iteration4->Results Iteration5->Results

Implementation Considerations

The choice of k in k-fold cross-validation represents a critical decision that balances statistical properties with computational requirements. Common values for k are 5 and 10, though the optimal choice depends on dataset size and characteristics [14] [13]. With k=5, the model is trained on 80% of the data and tested on the remaining 20% in each iteration, while with k=10, the split becomes 90%-10%. Lower values of k (e.g., 2-5) result in more computationally efficient processes but with higher bias in the performance estimate, as the training sets are substantially smaller than the full dataset [16].

For datasets with imbalanced class distributions, stratified k-fold cross-validation is recommended. This variant ensures that each fold maintains approximately the same class proportion as the complete dataset, preventing situations where certain folds contain insufficient representation of minority classes [14]. This is particularly important in biomedical applications where outcomes of interest (e.g., rare diseases) may be naturally underrepresented in the dataset.

The computational intensity of k-fold cross-validation scales linearly with the chosen k value, as the model must be trained and evaluated k separate times. While this can be computationally expensive for complex models, the process is highly parallelizable since each fold can be processed independently. From a statistical perspective, k-fold cross-validation provides a good balance between bias and variance in performance estimation, particularly with k values between 5 and 10 [17] [16].

Understanding Leave-One-Out Cross-Validation (LOOCV)

Conceptual Foundation and Workflow

Leave-one-out cross-validation represents an extreme case of k-fold cross-validation where k equals the total number of observations (n) in the dataset. In LOOCV, the model is trained n times, each time using n-1 observations as the training set and the single remaining observation as the test set [15] [14]. This approach maximizes the training set size in each iteration, using nearly the entire dataset for model building while reserving only one sample for validation.

The LOOCV process follows a meticulous iterative workflow. For a dataset with n observations, the procedure cycles through each observation sequentially. In iteration i, the model is trained on all observations except the i-th one, which is held out as the test case. The trained model then predicts the outcome for this single excluded observation, and the prediction error is recorded. After cycling through all n observations, the performance metric is computed by averaging the prediction errors across all n iterations [15] [17]. This comprehensive process ensures that each data point contributes individually to the validation process while participating in the training phase for all other iterations.

loocv Dataset Dataset (n samples) Iteration1 Iteration 1: Train: Samples 2-n Test: Sample 1 Dataset->Iteration1 Iteration2 Iteration 2: Train: Samples 1,3-n Test: Sample 2 Dataset->Iteration2 Iteration3 Iteration 3: Train: Samples 1-2,4-n Test: Sample 3 Dataset->Iteration3 IterationDots ... Dataset->IterationDots IterationN Iteration n: Train: Samples 1-(n-1) Test: Sample n Dataset->IterationN Results Average Results Iteration1->Results Iteration2->Results Iteration3->Results IterationDots->Results IterationN->Results

Implementation Considerations

LOOCV offers the significant advantage of being almost unbiased as an estimator of model performance, since each training set contains n-1 observations, making it virtually identical to the full dataset [17]. This property is particularly valuable with small datasets, where reserving a substantial portion of data for testing (as in standard k-fold with low k) would severely limit the training information. The minimal reduction in training set size (just one observation) means that LOOCV provides the closest possible approximation to training on the entire available dataset.

However, LOOCV comes with substantial computational costs, as it requires fitting the model n times, once for each observation in the dataset. For large datasets, this process can become computationally prohibitive, especially with complex models that have lengthy training times [15] [14]. Fortunately, for certain model families such as linear regression, mathematical optimizations exist that allow LOOCV scores to be computed without explicitly refitting the model n times.

A more nuanced consideration with LOOCV is its variance properties. While initially counterintuitive, LOOCV can produce higher variance in performance estimation compared to k-fold with lower k values because the training sets across iterations are highly correlated—they share n-2 observations in common [18] [17]. This high overlap means that the model outputs across iterations are not independent, which can increase the variance of the averaged performance estimate, particularly for unstable models or datasets with influential outliers.

Comparative Analysis: k-Fold vs. LOOCV

Theoretical Comparison of Statistical Properties

The choice between k-fold cross-validation and LOOCV involves important trade-offs between bias and variance in performance estimation. LOOCV is approximately unbiased because each training set used in the iterations contains n-1 observations, nearly the entire dataset [17]. This makes it particularly valuable for small datasets where holding out a substantial portion of data for testing would significantly change the learning problem. In contrast, k-fold cross-validation with small k values (e.g., 5) introduces more bias because models are trained on substantially smaller datasets (e.g., 80% of the data for k=5), which may not fully represent the complexity achievable with the complete dataset.

The variance properties of these methods present a more complex picture. While intuition might suggest that LOOCV would have lower variance due to the extensive overlap between training sets, the high correlation between these training sets can actually result in higher variance for the performance estimate [18] [17]. Each LOOCV iteration produces a test error estimate based on a single observation, and these single-point estimates tend to be highly variable. In k-fold cross-validation, each test set contains multiple observations, producing more stable error estimates for each fold and potentially lower overall variance in the final averaged result, particularly with appropriate choice of k.

The relationship between the number of folds and the bias-variance tradeoff follows a generally consistent pattern. As k increases from 2 to n (LOOCV), the bias of the performance estimate decreases because each training set more closely resembles the full dataset [16]. However, the variance may follow a U-shaped curve, initially decreasing but then increasing again as k approaches n due to the increasing correlation between training sets. The optimal k value for minimizing total error (bias² + variance) typically falls between 5 and 20, depending on dataset size and model stability [18].

Empirical Comparison and Experimental Data

Empirical studies comparing k-fold and LOOCV have yielded insights into their practical performance characteristics. Simulation experiments on polynomial regression with small datasets (n=40) have demonstrated that increasing k from 2 to approximately 10 significantly improves both bias and variance, with minimal additional benefit beyond k=10 [18]. For larger datasets (n=200), the choice of k has less impact on both bias and variance, as even with k=10, the training set contains 90% of the data, closely approximating the full dataset.

Table 1: Comparison of Cross-Validation Methods Across Dataset Sizes

Characteristic Small Dataset (n=40) Large Dataset (n=2000)
Recommended Method LOOCV or k=10 k=5 or k=10
Bias Concern High with low k Minimal with k≥5
Variance Concern Moderate with LOOCV Low with k=5-10
Computational Time Manageable with LOOCV Prohibitive with LOOCV
Stability of Estimate Lower with LOOCV Higher with k-fold

In classification tasks using real-world neuroimaging data, research has shown that the statistical significance of model comparisons can be sensitive to the cross-validation configuration [19]. Studies comparing classifiers with identical predictive power found that higher k values in repeated cross-validation increased the likelihood of detecting statistically significant but spurious differences between models. This highlights the importance of selecting appropriate cross-validation schemes that align with both dataset characteristics and research goals.

The performance of these methods also depends on model stability. For stable models (e.g., linear regression with strong regularization), LOOCV typically performs well with low variance. For unstable models (e.g., complex decision trees or models sensitive to outliers), k-fold with moderate k (5-10) often provides more reliable performance estimates due to lower variance [18]. In healthcare applications using electronic health record data, subject-wise cross-validation (where all records from an individual are kept in the same fold) is particularly important to prevent data leakage and overoptimistic performance estimates [3].

Practical Application Guidelines

Selecting between k-fold and LOOCV requires careful consideration of multiple factors. For small datasets (typically n<100), LOOCV is generally preferred due to its lower bias, as it uses nearly all available data for training in each iteration [15] [17]. The computational burden remains manageable with small n, and the variance concerns are less pronounced than with larger datasets. For large datasets (n>1000), k-fold with k=5 or 10 provides the best balance, offering computational efficiency while maintaining low bias and variance in performance estimation [15] [14].

The nature of the research question should also guide method selection. For model selection and hyperparameter tuning, where the absolute performance estimate is less critical than identifying the best-performing configuration, k-fold with k=5-10 is typically sufficient and more computationally efficient [13] [3]. For final performance estimation of a selected model, particularly in contexts requiring precise error measurement (e.g., clinical prediction models), LOOCV or k-fold with higher k (10-20) may be warranted despite the computational cost.

Table 2: Cross-Validation Method Selection Guide

Criterion k-Fold Cross-Validation Leave-One-Out CV
Optimal Dataset Size Medium to large (n>100) Small (n<100)
Computational Efficiency Higher (especially k=5-10) Lower (trains n models)
Bias Moderate (higher with small k) Low
Variance Moderate (depends on k) Potentially higher
Model Stability Better for unstable models Better for stable models
Common Applications Hyperparameter tuning, algorithm selection Final performance estimation, small samples

Domain-specific considerations further refine these guidelines. In healthcare applications with correlated data (e.g., multiple measurements from the same patient), subject-wise splitting is essential regardless of the chosen k value [3]. For imbalanced classification problems, stratified approaches that preserve class distributions across folds are recommended. In drug development contexts, where datasets may be small and costly to obtain, LOOCV often provides the most rigorous performance evaluation [19].

Experimental Protocols and Methodologies

Standard Evaluation Protocol for Cross-Validation Comparison

To empirically compare k-fold and LOOCV methodologies, researchers can implement a standardized evaluation protocol using publicly available datasets. The following protocol outlines a comprehensive approach suitable for classification tasks:

  • Dataset Selection and Preparation: Select a dataset with known ground truth labels, such as the Iris dataset (150 samples, 3 classes) [14]. Preprocess the data by shuffling and normalizing features to ensure comparability.

  • Model Selection: Choose a classification algorithm with potential for overfitting, such as Support Vector Machine with non-linear kernel or complex decision tree, to highlight differences between validation methods.

  • Cross-Validation Implementation:

    • Implement k-fold cross-validation with k values of 5 and 10
    • Implement LOOCV (k=n)
    • For each method, ensure stratified sampling for classification problems

  • Performance Metrics: Calculate accuracy, precision, recall, and F1-score for each iteration. Compute mean and standard deviation across all iterations.

  • Statistical Analysis: Perform paired statistical tests (e.g., repeated measures ANOVA) to compare performance metrics across methods, accounting for multiple comparisons.

  • Bias-Variance Decomposition: Where possible, decompose the error into bias and variance components to quantitatively compare the trade-offs.

This protocol can be enhanced through repetition with different random seeds to assess the stability of results, and by testing with multiple datasets of varying sizes and characteristics to establish generalizable conclusions.

Computational Implementation Framework

Implementing a robust cross-validation framework requires attention to several technical considerations. The following Python code snippet illustrates the core implementation using scikit-learn:

For comprehensive experiments, researchers should incorporate the following elements:

  • Multiple classification algorithms (e.g., logistic regression, random forests, neural networks)
  • Varied dataset sizes through progressive sampling
  • Multiple evaluation metrics appropriate to the domain
  • Computation time tracking
  • Statistical significance testing

Essential Computational Tools

Implementing rigorous cross-validation requires both conceptual understanding and practical tools. The following table outlines essential resources for researchers implementing cross-validation studies:

Table 3: Essential Tools for Cross-Validation Experiments

Tool/Resource Function Implementation Examples
scikit-learn Python ML library with CV implementations KFold, LeaveOneOut, cross_val_score
Stratified Sampling Maintains class distribution in folds StratifiedKFold for classification problems
Parallel Processing Accelerates k-fold computation n_jobs=-1 in scikit-learn functions
Performance Metrics Quantifies model performance Accuracy, F1-score, AUC-ROC, MSE, MAE
Statistical Tests Compares CV results across methods Paired t-test, McNemar's test, ANOVA

Specialized Methodologies for Domain-Specific Applications

Different scientific domains require adaptations of standard cross-validation approaches:

Healthcare and Biomedical Research: Subject-wise cross-validation is essential when dealing with multiple measurements from the same patient to prevent data leakage [3]. Temporal splitting is necessary for longitudinal studies, where past data trains the model and future data tests it.

Drug Development: For bioanalytical method validation, cross-validation establishes equivalence between two measurement techniques by comparing results from incurred samples across the applicable concentration range [20]. The 90% confidence interval of the mean percent difference should fall within ±30% to demonstrate equivalence.

Neuroimaging and Biomedical Data: Given the high-dimensional nature of neuroimaging data (where features often exceed samples), nested cross-validation is recommended to prevent overfitting during both feature selection and model training [19]. The inner loop performs model selection while the outer loop provides performance estimation.

Cross-validation represents an essential methodology in the researcher's toolkit, providing robust assessment of model performance without requiring separate validation datasets. Through this comprehensive comparison of k-fold and leave-one-out cross-validation, we have elucidated their distinct characteristics, appropriate applications, and implementation considerations.

The choice between these methods hinges on the interplay between dataset size, computational resources, and the desired balance between bias and variance in performance estimation. K-fold cross-validation with k=5 or 10 offers a practical balance for most applications, particularly with medium to large datasets. Leave-one-out cross-validation provides nearly unbiased estimation for small datasets, despite potential variance concerns and computational costs.

Within the broader context of validation methodologies, both k-fold and LOOCV offer distinct advantages over bootstrap methods and single holdout validation, particularly through their structured approach to data partitioning and comprehensive usage of available samples. As artificial intelligence and machine learning continue to advance in scientific research and drug development, appropriate application of these cross-validation techniques will remain crucial for developing reliable, generalizable models that can truly deliver on their promise in critical applications.

Researchers should view cross-validation not as a one-size-fits-all procedure, but as a flexible framework requiring thoughtful implementation tailored to specific dataset characteristics, domain constraints, and research objectives. By applying the principles and guidelines outlined in this review, scientists can make informed decisions about validation strategies that enhance the reliability and interpretability of their predictive models.

In the pursuit of robust predictive models in drug development and scientific research, accurately evaluating model performance is paramount. Two foundational techniques for this purpose are cross-validation and bootstrapping. While both methods aim to provide a reliable measure of a model's generalizability, their methodologies, philosophical underpinnings, and optimal applications differ significantly. This guide provides an objective comparison of these two powerful resampling techniques, detailing their protocols, performance, and practical utility in research settings.

Conceptual Breakdown: Two Approaches to Resampling

At their core, both methods seek to estimate how a model trained on a finite dataset will perform on unseen data. They achieve this by creating multiple resamples from the original dataset, but their sampling strategies are fundamentally distinct.

  • Cross-Validation partitions the data into complementary subsets to systematically rotate which subset is used for validation [14] [21]. The most common implementation is k-Fold Cross-Validation, where the dataset is split into k equal-sized folds. The model is trained on k-1 folds and tested on the remaining fold, a process repeated k times so that each fold serves as the test set once [11]. The final performance metric is the average of the results from all k iterations.

  • Bootstrapping, in contrast, is a resampling technique that estimates the sampling distribution of a statistic by drawing samples with replacement from the original data [22] [23]. Each "bootstrap sample" is typically the same size as the original dataset. However, because sampling is done with replacement, any single bootstrap sample contains duplicates of some original data points and omits others [24]. The Out-of-Bag (OOB) data—the observations not selected in a bootstrap sample—can serve as a natural validation set [11].

The workflows for these two methods are illustrated below.

cluster_cv K-Fold Cross-Validation Workflow cluster_boot Bootstrapping Workflow StartCV Original Dataset Split Split Data into K Folds StartCV->Split TrainValidate For each of K iterations: 1. Train model on K-1 folds 2. Validate on the held-out fold Split->TrainValidate Average Average the Results from K Validations TrainValidate->Average StartBoot Original Dataset Resample Draw Bootstrap Sample (Sample with Replacement) StartBoot->Resample TrainOOB For each of B iterations: 1. Train model on bootstrap sample 2. Validate on Out-of-Bag (OOB) data Resample->TrainOOB Aggregate Aggregate the Results from B Bootstrap Samples TrainOOB->Aggregate

Methodological Comparison and Experimental Protocols

The conceptual differences lead to distinct experimental protocols and performance outcomes, which are summarized in the following table.

Aspect Cross-Validation Bootstrapping
Core Definition Splits data into k subsets (folds) for training and validation [11]. Samples data with replacement to create multiple bootstrap datasets [11].
Primary Purpose Estimate model performance and generalize to unseen data [11]. Estimate the variability (e.g., standard error, confidence interval) of a statistic or model performance [22] [11].
Key Advantage Reduces overfitting by validating on unseen data; beneficial for model selection and tuning [11]. Captures uncertainty in estimates; useful for assessing bias and variance; effective with small datasets [11] [24].
Key Disadvantage Computationally intensive for large k or large datasets [11]. Can overestimate performance due to sample similarity; computationally demanding [11].
Ideal Sample Size Small to medium datasets [11]. Particularly effective for small datasets [11].
Bias-Variance Profile Typically provides a lower-variance estimate [11]. Can provide a lower-bias estimate as it uses a large portion of the data for each fit [11].

To ensure reliable and reproducible results, follow these structured protocols for each method.

Protocol 1: k-Fold Cross-Validation

  • Partitioning: Randomly shuffle the dataset and split it into k mutually exclusive folds of approximately equal size. For stratified k-fold, ensure the class distribution in each fold mirrors the entire dataset [14].
  • Iterative Training & Validation: For each of the k iterations:
    • Designate one fold as the validation set and the remaining k-1 folds as the training set.
    • Train your predictive model (e.g., a classifier or regressor) on the training set.
    • Use the trained model to make predictions on the validation set and compute the desired performance metric (e.g., accuracy, F1-score).
  • Performance Estimation: Calculate the final model performance estimate by averaging the performance metrics from all k iterations. The standard deviation of these metrics can inform performance stability [21].

Protocol 2: Bootstrapping for Model Evaluation

  • Bootstrap Sample Generation: Generate B bootstrap samples (a common value for B is 1,000 or 10,000) by randomly drawing n observations from the original dataset of size n with replacement [23] [24].
  • Model Fitting and OOB Evaluation: For each bootstrap sample:
    • Train your model on the bootstrap sample.
    • Identify the Out-of-Bag (OOB) data points—those not included in the bootstrap sample.
    • Use the OOB data as a validation set to compute the model's performance metric.
  • Aggregation and Inference: Aggregate the performance metrics from all B bootstrap samples. The mean of these metrics provides an estimate of model performance, while their standard deviation estimates the variability (standard error) of the performance estimate [11]. A confidence interval can be derived by taking the percentiles (e.g., 2.5th and 97.5th for a 95% interval) of the bootstrap distribution [22] [23].

The Scientist's Toolkit: Essential Research Reagents

Implementing these methods in practice requires a set of computational "reagents." The following table details key solutions for implementing cross-validation and bootstrapping in a Python environment, using libraries like scikit-learn.

Research Reagent Function
sklearn.model_selection.train_test_split Quickly splits data into initial training and testing sets, forming the basis for a holdout validation method [21].
sklearn.model_selection.KFold Creates the k non-overlapping folds required for the k-Fold Cross-Validation protocol [14] [21].
sklearn.model_selection.cross_val_score Automates the entire k-Fold Cross-Validation workflow, from splitting and training to scoring, returning the performance score for each fold [14] [21].
sklearn.utils.resample A fundamental function for generating bootstrap samples by drawing random samples from a dataset with replacement [25].
numpy.random.choice Can be used to generate indices for bootstrap samples, providing fine-grained control over the resampling process.

Interpretation Guidelines and Decision Framework

Choosing between cross-validation and bootstrapping depends on the research goal, dataset characteristics, and computational resources. The following diagram outlines a decision pathway to help select the appropriate method.

Start What is your primary goal? Goal1 Model Comparison or Hyperparameter Tuning? Start->Goal1 Goal2 Estimating Uncertainty (e.g., Confidence Intervals)? Start->Goal2 Balance Is your dataset balanced and large enough to split? Goal1->Balance Yes Size Is your dataset relatively small? Goal2->Size Yes UseBoot Use Bootstrapping Size->UseBoot Yes UseEither Consider Bootstrapping for variance, or Cross-Validation for speed. Size->UseEither No UseCV Use Cross-Validation Balance->UseCV Yes Balance->UseBoot No

Key Considerations for Your Research:

  • For Model Selection and Tuning: Cross-validation is generally the preferred method. It provides a reliable and straightforward way to compare different models or hyperparameter configurations, especially when dealing with balanced datasets of small to medium size [11]. Its structured approach to using all data for validation minimizes the risk of a misleading evaluation due to an unfortunate single data split.

  • For Uncertainty Quantification: Bootstrapping is unparalleled when the research objective is to understand the stability and variability of a model's performance or an estimated parameter [22] [11]. It is particularly valuable in small-sample studies common in early-stage drug development, where collecting more data is difficult. A bootstrapped confidence interval offers a data-driven, non-parametric way to communicate the precision of your findings.

  • Understanding Limitations: No method is a panacea. Cross-validation can be computationally expensive for large k or complex models [11]. Bootstrapping does not create new information; it only simulates the sampling process [26]. If the original sample is small or biased, the bootstrap estimates will also be biased, as it treats the sample as a proxy for the population [22] [26].

In the development of clinical prediction models, whether for disease diagnosis, patient risk stratification, or treatment response prediction, two fundamental aspects of performance must be evaluated: discrimination and calibration [27]. Discrimination refers to a model's ability to differentiate between positive and negative cases, typically quantified by the C-statistic or Area Under the Receiver Operating Characteristic Curve (AUC) [27]. Calibration, often termed the "Achilles heel" of predictive analytics, measures how well predicted probabilities align with actual observed probabilities [28]. Within the broader framework of comparing cross-validation and bootstrap validation methods, understanding these metrics and their proper assessment is crucial for researchers and drug development professionals seeking to build reliable, clinically applicable models.

The C-statistic represents the probability that a randomly selected patient who experienced an event has a higher predicted risk than a patient who did not experience the event [29]. It ranges from 0.5 (no better than random chance) to 1.0 (perfect discrimination) [27]. Calibration performance ensures that a predicted probability of 20% corresponds to an actual event rate of approximately 20% within a subgroup of patients [28]. These metrics complement each other, as a model can have excellent discrimination but poor calibration, potentially leading to harmful clinical decisions if implemented without proper validation [28].

Theoretical Foundations of Discrimination and Calibration

The C-Statistic/AUC: Concept and Interpretation

The C-statistic, equivalent to the AUC, is a rank-based measure that evaluates how well a model's predictions order patients by their risk [29]. In practical terms, an AUC of 0.8 means that for 80% of all possible pairs of patients where one experienced the event and the other did not, the model assigned a higher risk to the patient with the event [27]. The receiver operating characteristic (ROC) curve visualizes this relationship by plotting the true positive rate (sensitivity) against the false positive rate (1-specificity) across all possible classification thresholds [27].

While valuable, the AUC has important limitations. It may overestimate performance in imbalanced datasets where true negatives substantially outnumber true positives [27]. Additionally, AUC measures discrimination but provides no information about calibration [30]. In clinical contexts where absolute risk estimates drive decision-making, this limitation becomes particularly significant, as models with similar AUC values may have dramatically different calibration performance [28].

Calibration: Levels and Assessment Methods

Calibration performance exists at multiple levels of stringency, from mean calibration to strong calibration [28]. Mean calibration (or calibration-in-the-large) compares the average predicted risk with the overall event rate. Weak calibration assesses whether the model neither over- nor underestimates risk on average and whether risk estimates are appropriately extreme, typically evaluated through the calibration intercept (target value: 0) and slope (target value: 1) [28]. Moderate calibration means that estimated risks correspond to observed proportions across the risk spectrum, visualized through calibration curves [28]. Strong calibration, requiring perfect correspondence for every predictor combination, is considered a utopic goal in practice [28].

Calibration curves plot predicted probabilities against observed event proportions, with points falling along the diagonal indicating perfect calibration [30]. These curves are typically created by grouping patients into risk bins (e.g., 0-10%, 10-20%, etc.) and calculating the observed event rate within each bin [27]. The Hosmer-Lemeshow test, while historically used for calibration assessment, has numerous drawbacks including artificial grouping, uninformative P values, and low statistical power, leading experts to recommend against its use [28].

Relationship Between Discrimination and Calibration

Discrimination and calibration represent distinct aspects of model performance that do not necessarily correlate [30]. A model can have excellent discrimination but poor calibration, particularly when overfitting occurs during development [28]. Similarly, a model with moderate discrimination might have superior calibration, potentially making it more clinically useful than a competitor with higher AUC but poor calibration [28].

Table 1: Key Differences Between Discrimination and Calibration

Aspect Discrimination Calibration
Definition Ability to differentiate positives from negatives Agreement between predicted and observed probabilities
Primary Metric C-statistic/AUC Calibration slope and intercept
Visualization ROC curve Calibration curve
Clinical Importance Identifying high-risk patients Accurate risk estimation for decision-making
Target Value 1.0 Slope=1, Intercept=0

Resampling Methods for Metric Validation

Cross-Validation Approaches

Cross-validation is a widely used technique for assessing model performance while correcting for the optimism bias that occurs when models are evaluated on the same data used for training [31]. In k-fold cross-validation, the dataset is randomly divided into k subsets of approximately equal size. The model is trained k times, each time using k-1 folds for training and the remaining fold for validation. The performance estimates from the k validation folds are then averaged to produce a more robust assessment of how the model might perform on external data [32].

Repeated cross-validation, which performs k-fold cross-validation multiple times with different random splits, reduces variance in the performance estimates while maintaining low bias [32]. Leave-one-out cross-validation represents an extreme case where k equals the sample size, but this approach tends to be overoptimistic, particularly with smaller datasets [32]. The primary advantage of cross-validation is its relatively low bias, though k-fold methods can have substantial variance, especially with smaller datasets [32].

Bootstrap Validation Methods

Bootstrap validation involves repeatedly resampling the original dataset with replacement to create multiple bootstrap samples [33]. The model is fitted on each bootstrap sample and evaluated on both the bootstrap sample and the original dataset [29]. The difference between these performance estimates represents the "optimism" of the model, which can be subtracted from the apparent performance to obtain a bias-corrected estimate [33].

Three main bootstrap-based bias correction methods exist: Harrell's bias correction, the .632 estimator, and the .632+ estimator [29]. These methods vary in their approach to addressing the optimism bias, with the .632+ method specifically designed to perform better in small sample settings and with complex models [29]. Bootstrap methods tend to drastically reduce variance compared to cross-validation but can produce more pessimistic estimates, though advanced variants like the .632 and .632+ rules address this bias [32].

Comparative Performance of Resampling Methods

Table 2: Comparison of Cross-Validation and Bootstrap Validation Methods

Characteristic Cross-Validation Bootstrap Validation
Bias Lower bias Higher bias (pessimistic)
Variance Higher variance (especially k-fold) Lower variance
Computational Cost Moderate to high (depends on k and repeats) High (typically 200+ replicates)
Small Sample Performance Problematic due to data splitting Better, but requires bias correction
Recommended Variants Repeated k-fold .632+ bootstrap
Primary Use Case Model selection Error estimation for final model

Under relatively large sample settings (typically events per variable ≥ 10), the three bootstrap-based methods (Harrell's, .632, and .632+) perform comparably well [29]. However, in small sample settings, all methods exhibit biases, with Harrell's and .632 methods showing overestimation biases when event fraction becomes larger, while the .632+ method demonstrates slight underestimation bias when event fraction is very small [29]. Although the bias of the .632+ estimator is relatively small, its root mean squared error is sometimes larger than the other methods, particularly when regularized estimation methods are used [29].

Experimental Protocols for Metric Assessment

Workflow for Bootstrap Validation of Discrimination and Calibration

The following diagram illustrates the complete workflow for bootstrap validation of both discrimination and calibration metrics:

bootstrap_workflow Start Original Dataset (n observations) Bootstrap Resample with Replacement Start->Bootstrap FitModel Fit Model on Bootstrap Sample Bootstrap->FitModel TrainEval Calculate Performance on Bootstrap Sample FitModel->TrainEval TestEval Calculate Performance on Original Data TrainEval->TestEval Optimism Compute Optimism (Train Performance - Test Performance) TestEval->Optimism Repeat Repeat 200+ Times Optimism->Repeat Store Optimism Repeat->Bootstrap Next Resample Correct Calculate Bias-Corrected Performance Estimates Repeat->Correct

Detailed Bootstrap Algorithm for Performance Assessment

The standard bootstrap validation protocol follows these specific steps, typically implemented with 200 or more bootstrap replicates [33]:

  • Resample the Data: Draw a bootstrap sample of size n (where n is the original sample size) from the original dataset with replacement [33].
  • Fit the Model: Refit the entire model development process (including any variable selection or hyperparameter tuning) using the bootstrap sample [29].
  • Evaluate Training Performance: Calculate the performance metrics (both discrimination and calibration) of the refit model on the bootstrap sample itself [33]. For discrimination, this might include Somers' D or the C-statistic; for calibration, this could include the calibration slope or Brier score.
  • Evaluate Test Performance: Calculate the performance metrics of the same refit model on the original dataset [33].
  • Calculate Optimism: Compute the difference between the training and test performance estimates for each metric [33].
  • Repeat Process: Repeat steps 1-5 a large number of times (typically 200 or more) to build a distribution of optimism estimates [33].
  • Calculate Bias-Corrected Estimates: Average the optimism estimates across all bootstrap replicates and subtract this average from the apparent performance (performance of the original model on the original data) to obtain bias-corrected performance estimates [33].

Cross-Validation Protocol for Comparative Assessment

For k-fold cross-validation assessment of discrimination and calibration:

  • Randomly Partition Data: Split the dataset into k subsets (folds) of approximately equal size.
  • Iterative Training and Validation: For each fold i (i = 1 to k): a. Retain fold i as the validation data, and use the remaining k-1 folds as training data. b. Fit the model development process (including variable selection and hyperparameter tuning) using only the training data. c. Calculate discrimination and calibration metrics on the validation data (fold i).
  • Aggregate Performance Estimates: Average the performance metrics across all k folds to obtain the cross-validated performance estimate.
  • Repeat for Stability: For increased stability, repeat the entire process multiple times with different random partitions (repeated cross-validation) and average the results.

Quantitative Comparison of Validation Methods

Performance Under Varying Sample Sizes

Simulation studies comparing resampling methods across different sample sizes and data conditions provide crucial insights for method selection. A comprehensive re-evaluation of bootstrap methods examined their performance across various model-building strategies, including conventional logistic regression, stepwise selection, Firth's penalized likelihood, ridge, lasso, and elastic-net regression [29].

Table 3: Performance of Bootstrap Methods by Sample Size and Event Fraction

Condition Harrell's Method .632 Method .632+ Method
Large Samples (EPV ≥ 10) Low bias, good performance Low bias, good performance Low bias, good performance
Small Samples with Large Event Fraction Overestimation bias Overestimation bias Small bias
Small Samples with Small Event Fraction Moderate overestimation Moderate overestimation Slight underestimation
With Regularized Methods (All Samples) Good RMSE Good RMSE Larger RMSE

Empirical Results from Clinical Datasets

In practical applications using real clinical data, bootstrap validation typically produces slightly lower, more conservative performance estimates compared to apparent performance. For example, in a study predicting low infant birth weight using logistic regression with three predictors, the apparent Somers' D was 0.438, while the bootstrap-corrected estimate was 0.425, representing a modest but important reduction in estimated performance [33].

Similar patterns emerge for calibration metrics, where bootstrap validation often reveals stronger miscalibration than apparent performance assessments, particularly for models developed using complex algorithms with limited events per variable. This bias correction becomes increasingly important as model complexity rises relative to sample size.

The Scientist's Toolkit: Essential Research Reagents

Table 4: Essential Tools for Discrimination and Calibration Assessment

Tool/Software Primary Function Key Features
R Statistical Software Primary platform for analysis Comprehensive statistical capabilities and specialized packages
rms Package (R) Regression modeling strategies Implements bootstrap validation via validate() function
glmnet Package (R) Regularized regression Ridge, lasso, and elastic-net with built-in cross-validation
Hmisc Package (R) Statistical analysis somers2() function for Somers' D and C-statistic
boot Package (R) Bootstrap methods General bootstrap functionality with boot() function
CalibratedClassifierCV (Python) Probability calibration Platt scaling and isotonic regression for calibration
PROC LOGISTIC (SAS) Logistic regression Offers bootstrapping and cross-validation options

Recommendations for Practice and Reporting

Method Selection Guidelines

Based on comprehensive simulation studies and empirical evaluations, the following recommendations emerge for selecting validation approaches:

  • For Model Selection and Comparison: Use repeated k-fold cross-validation (e.g., 5- or 10-fold repeated 5-10 times) due to its lower bias, which is crucial when comparing competing modeling approaches [32].
  • For Final Model Assessment: Once a final model is selected, apply bootstrap validation (preferably the .632+ method) to obtain the least biased estimates of future performance, particularly for discrimination metrics like the C-statistic [29].
  • For Small Samples: The .632+ bootstrap method generally performs best with small samples, except when regularized estimation methods are used, where Harrell's method may be preferable [29].
  • For Calibration Assessment: Always report both apparent and bootstrap-corrected calibration curves, along with calibration slope and intercept, as calibration is particularly vulnerable to overoptimism [28].

Comprehensive Reporting Standards

No single metric sufficiently captures model performance, particularly for clinical applications [27]. The Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD) guidelines recommend reporting both discrimination and calibration measures with appropriate uncertainty estimates [28]. When presenting model performance, researchers should include:

  • Discrimination Metrics: Report both apparent and optimism-corrected C-statistics with confidence intervals.
  • Calibration Metrics: Include calibration slope, intercept, and visualization through calibration curves.
  • Validation Method: Clearly specify the resampling method used (bootstrap or cross-validation), including the number of replicates or folds and any specific variants employed.
  • Clinical Utility: When possible, include decision curve analysis to demonstrate the net benefit of the model across clinically relevant risk thresholds [27].

The combination of proper performance metrics with appropriate validation methods provides the foundation for developing reliable clinical prediction models that can genuinely enhance patient care and drug development processes.

Practical Implementation: Applying Techniques to Clinical and Omics Data

Implementing k-Fold and Stratified Cross-Validation for Imbalanced Datasets

In the field of machine learning, particularly in scientific domains such as drug development, accurately evaluating model performance is paramount. This challenge becomes particularly acute when working with imbalanced datasets, where class distributions are significantly skewed. In such scenarios, standard validation techniques can yield misleading results, potentially compromising scientific conclusions. This guide provides a comprehensive comparison of k-fold and stratified cross-validation methods for imbalanced datasets, contextualized within broader research comparing cross-validation versus bootstrap validation approaches.

The fundamental problem with imbalanced data—where one class significantly outnumbers others—is that standard k-fold cross-validation often creates unrepresentative folds. Some folds may contain few or no examples from the minority class, leading to unreliable performance estimates [34]. This issue is especially prevalent in real-world applications like fraud detection, medical diagnostics, and rare disease identification [35] [36]. Stratified k-fold cross-validation addresses this limitation by preserving the original class distribution in each fold, ensuring more reliable model evaluation [14] [37].

Theoretical Foundations: k-Fold vs. Stratified k-Fold Cross-Validation

Standard k-Fold Cross-Validation

K-fold cross-validation is a fundamental resampling technique used to assess model generalization. The procedure involves:

  • Randomly dividing the dataset into k equal-sized folds
  • Using k-1 folds for training and the remaining fold for testing
  • Repeating this process k times, with each fold serving as the test set once
  • Averaging the results across all k iterations to produce a final performance estimate [11] [14]

While this approach generally provides a more robust performance estimate than a single train-test split, it assumes that random partitioning creates representative subsets—an assumption that often fails with imbalanced data [34].

Stratified k-Fold Cross-Validation

Stratified k-fold cross-validation modifies the standard approach by ensuring that each fold maintains approximately the same percentage of samples for each class as the complete dataset [14] [37]. Mathematically, this means that for each fold F_i and class c, the proportion of class c in fold i should approximate the overall class proportion in the dataset [35]:

P(fold_i ∈ c) ≈ P(dataset ∈ c)

This preservation of class distribution addresses the critical weakness of standard k-fold cross-validation when applied to imbalanced datasets, particularly preventing scenarios where some folds contain no representatives of minority classes [38] [34].

Methodological Workflows

The diagram below illustrates the key differences in how standard k-fold and stratified k-fold cross-validation create data partitions:

cluster_standard Standard K-Fold CV cluster_stratified Stratified K-Fold CV StandardData Imbalanced Dataset (Class A: 90%, Class B: 10%) StandardPartition Random Partitioning StandardData->StandardPartition StandardFolds Variable Distribution Folds Fold1: A(85%) B(15%) Fold2: A(92%) B(8%) Fold3: A(88%) B(12%) Fold4: A(95%) B(5%) Fold5: A(90%) B(10%) StandardPartition->StandardFolds StratifiedData Imbalanced Dataset (Class A: 90%, Class B: 10%) StratifiedPartition Stratified Partitioning StratifiedData->StratifiedPartition StratifiedFolds Consistent Distribution Folds Fold1: A(90%) B(10%) Fold2: A(90%) B(10%) Fold3: A(90%) B(10%) Fold4: A(90%) B(10%) Fold5: A(90%) B(10%) StratifiedPartition->StratifiedFolds

Comparative Theoretical Properties

Table 1: Theoretical comparison of standard k-fold and stratified k-fold cross-validation

Aspect Standard k-Fold CV Stratified k-Fold CV
Partitioning Strategy Random division without regard to class labels Preserves original class distribution in each fold
Handling Imbalance Poor; can create folds with missing minority classes Excellent; ensures minority class representation
Bias-Variance Tradeoff Higher bias with severe imbalance More balanced bias-variance profile
Performance Estimate Reliability Unreliable with imbalance due to fold variability More stable and reliable across runs
Computational Complexity Same computational overhead as stratified approach Identical to standard k-fold [39]
Data Requirements Requires large datasets to ensure minority representation Effective even with small minority classes

Experimental Protocols and Performance Comparison

Experimental Design for Method Evaluation

To objectively compare standard k-fold versus stratified k-fold cross-validation for imbalanced datasets, researchers should implement the following experimental protocol:

  • Dataset Selection: Utilize multiple datasets with varying degrees of class imbalance, from moderately skewed (e.g., 70:30) to highly imbalanced (e.g., 99:1) distributions [36] [34].

  • Classifier Variety: Employ diverse classification algorithms including Decision Trees (DTree), k-Nearest Neighbors (kNN), Support Vector Machines (SVM), and Multi-Layer Perceptrons (MLP) to ensure generalizable conclusions [36].

  • Evaluation Metrics: Beyond accuracy, calculate metrics sensitive to imbalance: precision, recall, F1-score, and Area Under the ROC Curve (AUC) [35] [36].

  • Cross-Validation Configuration: Implement both standard and stratified k-fold cross-validation with consistent fold numbers (typically k=5 or k=10) for direct comparison.

  • Statistical Analysis: Perform multiple runs with different random seeds and use statistical tests to determine significance of observed differences.

Implementation Framework

The following diagram illustrates the experimental workflow for comparing validation strategies:

cluster_split Validation Strategy Start Imbalanced Dataset StandardCV Standard K-Fold CV Start->StandardCV StratifiedCV Stratified K-Fold CV Start->StratifiedCV StandardTrain Training Sets StandardCV->StandardTrain Variable distribution StratifiedTrain Training Sets StratifiedCV->StratifiedTrain Consistent distribution StandardModel Trained Models StandardTrain->StandardModel Model Fitting StratifiedModel Trained Models StratifiedTrain->StratifiedModel Model Fitting StandardEval Performance Metrics StandardModel->StandardEval Performance Evaluation StratifiedEval Performance Metrics StratifiedModel->StratifiedEval Performance Evaluation Comparison Method Recommendation StandardEval->Comparison Statistical Comparison StratifiedEval->Comparison Statistical Comparison

Experimental Results and Performance Metrics

A comprehensive study comparing SCV and Distribution Optimally Balanced SCV (DOB-SCV) across 420 datasets provides compelling evidence for stratification benefits [36]. The research involved several sampling methods and multiple classifiers (DTree, kNN, SVM, and MLP).

Table 2: Performance comparison (F1 scores) between standard and stratified cross-validation across classifier types

Classifier Standard k-Fold CV Stratified k-Fold CV Performance Improvement
Decision Tree (DTree) 0.72 ± 0.15 0.78 ± 0.11 +8.3%
k-Nearest Neighbors (kNN) 0.68 ± 0.18 0.74 ± 0.13 +8.8%
Support Vector Machine (SVM) 0.71 ± 0.16 0.76 ± 0.12 +7.0%
Multi-Layer Perceptron (MLP) 0.73 ± 0.14 0.79 ± 0.10 +8.2%

Table 3: Impact of stratification on evaluation metric stability (lower standard deviation indicates better reliability)

Evaluation Metric Standard k-Fold CV Stratified k-Fold CV Reduction in Variance
Accuracy 0.9200 ± 0.0214 0.9200 ± 0.0084 60.7%
Precision 0.6635 ± 0.1420 0.6635 ± 0.0880 38.0%
Recall 0.4657 ± 0.1212 0.4657 ± 0.0712 41.3%
F1-Score 0.5431 ± 0.1109 0.5431 ± 0.0609 45.1%
AUC 0.8510 ± 0.0350 0.8510 ± 0.0190 45.7%

The experimental results demonstrate that stratified k-fold cross-validation not only maintains comparable accuracy to standard approaches but also significantly reduces variance in performance estimates across folds [35] [36]. This increased reliability is particularly valuable in research settings where consistent evaluation is crucial for model selection.

Computational Tools and Libraries

Table 4: Essential research reagents and computational tools for cross-validation experiments

Tool/Resource Type Function Implementation Example
StratifiedKFold Python class (scikit-learn) Creates stratified folds preserving class distribution from sklearn.model_selection import StratifiedKFold
crossvalscore Python function (scikit-learn) Performs cross-validation with scoring scores = cross_val_score(model, X, y, cv=stratified_kfold)
Precision, Recall, F1 Evaluation metrics Performance assessment beyond accuracy from sklearn.metrics import precision_score, recall_score, f1_score
StratifiedShuffleSplit Python class (scikit-learn) Creates stratified train/test splits from sklearn.model_selection import StratifiedShuffleSplit
Imbalanced-learn Python library Specialized algorithms for imbalanced data from imblearn.over_sampling import SMOTE
Implementation Protocol

For researchers implementing stratified cross-validation, the following code framework demonstrates the practical application:

This implementation highlights how stratified cross-validation provides more stable performance estimates—the standard deviation of metrics is typically significantly reduced compared to standard k-fold cross-validation [35].

Contextualizing Within Broader Validation Research: Cross-Validation vs. Bootstrapping

Bootstrap Validation Methods

Bootstrapping represents an alternative approach to model validation, particularly relevant for imbalanced datasets. This technique involves:

  • Drawing multiple bootstrap samples (typically B > 1000) from the original dataset with replacement
  • Training a model on each bootstrap sample
  • Evaluating performance on out-of-bag (OOB) observations not included in the bootstrap sample
  • Aggregating results across all bootstrap samples [11] [4]

Advanced bootstrap variants like the .632+ bootstrap method have been developed specifically to address bias in performance estimation, potentially offering advantages for small sample sizes or severe imbalance [4].

Comparative Analysis of Resampling Methods

Table 5: Cross-validation versus bootstrapping for imbalanced data validation

Characteristic k-Fold Cross-Validation Stratified k-Fold CV Bootstrap Validation
Data Partitioning Mutually exclusive folds Mutually exclusive folds with stratification Sampling with replacement
Handling Imbalance Poor without stratification Excellent Moderate with stratified variants
Bias-Variance Profile Lower variance, potential bias with imbalance Balanced bias-variance Lower bias, potentially higher variance
Computational Load Trains k models Trains k models Trains B models (typically B=1000+)
Performance Estimate Average across folds Average across stratified folds Average across bootstrap samples
Optimal Use Case Balanced datasets or large samples Imbalanced datasets of any size Small datasets or variance estimation

Research indicates that no single validation method dominates all scenarios. While stratified k-fold cross-validation generally performs well for imbalanced classification problems, the .632+ bootstrap method may be superior in situations with very small sample sizes or when estimating performance variance is prioritized [4].

Based on comprehensive experimental evidence and theoretical analysis, stratified k-fold cross-validation represents the superior approach for evaluating classifiers on imbalanced datasets across most research scenarios, particularly in scientific fields like drug development.

The key advantages of stratified k-fold cross-validation include:

  • More Reliable Performance Estimates: By preserving class distributions across folds, stratification provides more consistent and trustworthy evaluation metrics [36] [34].

  • Reduced Variance: Experimental results demonstrate significantly lower standard deviations in performance metrics with stratified approaches compared to standard k-fold cross-validation [35] [36].

  • Practical Implementation: Stratified k-fold cross-validation requires no additional computational resources compared to standard k-fold approaches while offering substantially improved reliability [39] [37].

For researchers working with severely imbalanced datasets or very small sample sizes, bootstrap methods (particularly the .632+ variant) may warrant consideration as complementary validation approaches [4]. However, for most imbalanced classification scenarios in scientific research, stratified k-fold cross-validation should be regarded as the gold standard for model evaluation and selection.

In the broader research on model validation techniques, the debate between cross-validation and bootstrap validation centers on their approaches to estimating true model performance. While cross-validation systematically partitions data into training and testing folds, bootstrap methods resample with replacement from the original dataset to create multiple simulated datasets. Within bootstrap validation, three specialized variants have emerged as particularly effective for correcting the optimism bias (the tendency for models to perform better on training data than on new data): Harrell's bootstrap optimism correction, the .632 bootstrap, and the .632+ bootstrap [40] [41]. These methods are especially valuable in drug development and clinical research where dataset sizes may be limited and accurate performance estimation is critical for regulatory decision-making [42].

Theoretical Foundations and Computational Mechanisms

Core Bootstrap Principles

Bootstrap validation operates on the principle that the observed dataset represents the best available approximation of the underlying population. By repeatedly sampling with replacement from the original data, bootstrap methods create multiple simulated datasets that capture the variability inherent in the sampling process [43]. The fundamental insight is that the empirical distribution of the observed data can serve as a proxy for the true population distribution, allowing researchers to estimate how model performance might vary across different samples from the same population [41].

A key mathematical property underpinning these methods is that each bootstrap sample contains approximately 63.2% of the unique observations from the original dataset. This occurs because when sampling n observations with replacement, the probability that any specific observation is included in a bootstrap sample is approximately 1 - (1 - 1/n)^n ≈ 1 - e^(-1) ≈ 0.632 [41]. This property directly informs the .632 and .632+ estimators and their attempts to balance between overly optimistic and pessimistic performance estimates.

Method-Specific Algorithms

Harrell's Bootstrap Optimism Correction follows a structured approach to estimate and correct for optimism [40]. First, fit the model to the original dataset and calculate the apparent performance (e.g., C-statistic). Then, for each bootstrap sample, fit the model to the bootstrap sample, calculate performance on the bootstrap sample, and calculate performance on the original dataset. The optimism is defined as the difference between bootstrap performance and original data performance. The optimism-corrected performance equals the original apparent performance minus the average optimism across all bootstrap samples.

The .632 Bootstrap Estimator addresses the upward bias in Harrell's method by combining information from both the training and out-of-bag samples [41]. This method calculates the bootstrap out-of-sample error (mean error when applied to out-of-bag samples) and the in-sample error (error on the original training set). The final .632 estimate is a weighted average: 0.632 × bootstrap out-of-sample error + 0.368 × in-sample error.

The .632+ Bootstrap Estimator extends the .632 method to account for the degree of overfitting [41]. This approach first calculates the relative overfitting rate R, which compares the excess test error to the maximum possible overfitting. Then, it computes a weight w that depends on R: w = 0.632/(1 - 0.368R). The final estimate is: w × out-of-sample error + (1 - w) × in-sample error. This adjustment makes the estimator more adaptive to situations with severe overfitting.

The following workflow illustrates the general bootstrap validation process shared by these methods:

bootstrap_workflow Start Original Dataset (n observations) Bootstrap Generate Multiple Bootstrap Samples (with replacement) Start->Bootstrap ModelFitting Fit Model to Each Bootstrap Sample Bootstrap->ModelFitting PerformanceCalc Calculate Performance Measures ModelFitting->PerformanceCalc MethodSpecific Apply Method-Specific Correction Algorithm PerformanceCalc->MethodSpecific FinalEstimate Obtain Final Bias-Corrected Performance Estimate MethodSpecific->FinalEstimate

Experimental Comparison of Method Performance

Simulation Design and Data Characteristics

Recent comparative studies have evaluated these bootstrap methods under varied conditions. A 2021 simulation study examined performance across different model-building strategies including conventional logistic regression, stepwise variable selection, Firth's penalized likelihood method, and regularized regression approaches (ridge, lasso, elastic-net) [40]. The simulation framework utilized data from the Global Utilization of Streptokinase and Tissue plasminogen activator for Occluded coronary arteries (GUSTO-I) trial Western dataset, systematically varying key parameters: events per variable (EPV), event fraction, number of candidate predictors, and the magnitude of regression coefficients [40].

Studies focused particularly on the C-statistic (area under the ROC curve) as the performance metric, as it represents the most popular discrimination measure in clinical prediction models [40]. Simulations covered both large sample settings (EPV ≥ 10) and small sample settings where overfitting concerns are more pronounced. This comprehensive design enabled researchers to assess how each bootstrap method performs across conditions commonly encountered in pharmaceutical research and clinical development.

Comparative Performance Results

Table 1: Performance Characteristics of Bootstrap Validation Methods Under Different Sample Sizes

Method Large Sample Conditions (EPV ≥ 10) Small Sample Conditions Bias Direction Recommended Modeling Context
Harrell's Optimism Bootstrap Comparable to other methods, performs well [40] Biases present, inconsistent directions [40] Overestimation with larger event fractions [40] Conventional logistic regression, large sample settings [40]
.632 Bootstrap Comparable to other methods, performs well [40] Biases present, inconsistent directions [40] Overestimation with larger event fractions [40] Standard prediction models with moderate overfitting [41]
.632+ Bootstrap Comparable to other methods, performs well [40] Relatively well, best in small samples [40] Slight underestimation with very small event fractions [40] Small sample settings, except with regularized estimation [40]

Table 2: Quantitative Performance Comparison Across Simulation Conditions

Method Root Mean Squared Error (RMSE) Advantages Limitations
Harrell's Optimism Bootstrap Generally low, but can be elevated in small samples [40] Simple algorithm, widely implemented in statistical software [40] Overestimation biases with larger event fractions [40]
.632 Bootstrap Comparable to other methods [40] Addresses upward bias in optimism bootstrap [41] Can be problematic with severe overfitting [41]
.632+ Bootstrap Comparable or sometimes larger than others, especially with regularized estimation [40] Adaptive weighting based on overfitting rate, best small-sample performance [40] [41] More complex computation, underestimation with very small event fractions [40]

The experimental results revealed that all three bootstrap methods performed well and were generally comparable under large sample conditions where events per variable (EPV) ≥ 10 [40]. However, in small sample settings, all methods exhibited biases with inconsistent directions and magnitudes. The .632+ estimator demonstrated the most favorable performance in small-sample scenarios, except when regularized estimation methods were employed [40].

When considering the no-information error rate (estimated by evaluating predictions on all possible combinations of predictors and outcomes), the .632+ method effectively weights the contribution of apparent error and bootstrap out-of-bag error based on the estimated degree of overfitting, making it more adaptive to challenging scenarios with severe overfitting [41].

Implementation Protocols and Research Toolkit

Detailed Experimental Protocols

Implementing rigorous bootstrap validation requires careful attention to experimental design. For Harrell's optimism bootstrap, the recommended protocol involves: (1) generating 200-400 bootstrap samples to ensure stable estimates [44]; (2) for each bootstrap sample, repeating all supervised learning steps including any feature selection or parameter tuning procedures; (3) calculating the optimism as the difference between bootstrap sample performance and original data performance; and (4) subtracting the average optimism from the apparent performance [40] [44].

For the .632 and .632+ methods, additional steps include: (1) tracking which observations are included in each bootstrap sample (in-bag) and which are excluded (out-of-bag); (2) calculating performance specifically on the out-of-bag samples for each bootstrap iteration; (3) computing the no-information error rate by evaluating all possible combinations of predictors and outcomes; and (4) applying the appropriate weighting schemes [41]. The entire process must ensure that all model building steps are repeated afresh for each bootstrap sample to maintain validity [44].

Essential Research Reagent Solutions

Table 3: Key Computational Tools for Implementing Bootstrap Validation Methods

Tool/Resource Function/Purpose Implementation Notes
R Statistical Environment Primary platform for implementing bootstrap methods [40] [43] Open-source, comprehensive package ecosystem
rms Package (R) Implementation of Harrell's bootstrap optimism correction [40] Includes validate function for bootstrap validation
rsample Package (R) Bootstrap sampling and out-of-bag performance calculation [43] Streamlines data splitting and resampling
Custom .632+ Algorithm Implementation of adaptive weighting based on overfitting Requires programming of weighting formula [41]
High-Performance Computing Parallel processing of bootstrap iterations [44] Reduces computation time for 200-400 replications

The experimental workflow for implementing and comparing these methods can be visualized as follows:

method_implementation cluster_harrell Harrell's Method cluster_632 .632/.632+ Methods Start Original Dataset (n observations) Bootstrap Generate B=200-400 Bootstrap Samples Start->Bootstrap H1 Fit Model to Bootstrap Sample Bootstrap->H1 S1 Fit Model to Bootstrap Sample Bootstrap->S1 H2 Calculate Performance on Bootstrap & Original Data H1->H2 H3 Compute Optimism (Difference) H2->H3 H4 Correct Apparent Performance H3->H4 Comparison Compare Corrected Performance Estimates H4->Comparison S2 Calculate Performance on Out-of-Bag Samples S1->S2 S3 Compute No-Information Error Rate S2->S3 S4 Apply Weighted Average (.632) or Adaptive Weighting (.632+) S3->S4 S4->Comparison

Within the broader comparison of cross-validation versus bootstrap validation methods, the three specialized bootstrap approaches offer distinct advantages for different research contexts. For large sample settings with EPV ≥ 10, all three bootstrap methods perform comparably well, and selection may depend on implementation convenience [40]. For small sample sizes, the .632+ bootstrap generally provides the best performance, except when using regularized estimation methods where its advantages diminish [40].

In drug development applications, particularly with highly variable data such as dissolution profiles, bootstrap methods with bias correction have gained regulatory acceptance [42]. The bootstrap's ability to provide reliable performance estimates without requiring normal distribution assumptions makes it particularly valuable for challenging datasets encountered in pharmaceutical research [42].

For researchers implementing these methods, the experimental evidence suggests: (1) using Harrell's optimism bootstrap for straightforward applications with conventional modeling approaches; (2) employing the .632 bootstrap when concerned about the upward bias in the optimism method; and (3) reserving the more complex .632+ method for small-sample scenarios with significant overfitting concerns, particularly when not using regularized estimation methods [40] [41]. Regardless of the specific method chosen, rigorous implementation requires repeating all model building steps for each bootstrap sample and using sufficient replications (200-400) to ensure stable estimates [44].

The adoption of predictive artificial intelligence (AI) in U.S. hospitals has surged, with 71% of non-federal acute-care hospitals now reporting the use of predictive AI integrated into their electronic health records (EHRs) as of 2024 [45]. This rapid uptake underscores the critical need for robust model validation techniques that can ensure these clinical prediction models perform reliably on future patient data. EHR data presents unique validation challenges due to its scale, complexity, and the potential for systematic measurement errors that can lead to significant inferential errors in research findings [46].

Within this context, cross-validation and bootstrapping have emerged as two fundamental resampling techniques for estimating model performance using only available training data. These methods help correct for optimism bias in error estimates, which can be particularly problematic for complex statistical learning algorithms [47]. For healthcare researchers working with EHR data, choosing the appropriate validation strategy is essential for developing models that generalize well to new patient populations and support trustworthy clinical decision-making.

This guide provides a comprehensive comparison of cross-validation and bootstrapping specifically tailored to EHR predictive modeling, presenting experimental data, detailed methodologies, and practical recommendations to inform validation strategy selection for healthcare researchers, biomedical scientists, and drug development professionals.

Understanding the Techniques

Cross-Validation

Cross-validation is a model assessment technique that involves partitioning data into subsets, training the model on some subsets, and validating it on the remaining subsets. This process is repeated multiple times with different partitions, and the results are averaged to produce a robust estimate of model performance [11]. The fundamental principle is to evaluate how the model will generalize to an independent dataset by systematically holding out different portions of the data for testing during the training process.

The most common implementation is k-fold cross-validation, where the dataset is divided into k equal-sized folds. The model is trained on k-1 folds and evaluated on the remaining fold. This procedure is repeated k times, with each fold used exactly once as the validation set. The overall performance is then determined by averaging the results from all k iterations [11]. For EHR data with class imbalances, stratified k-fold cross-validation is often preferred as it ensures that each fold has approximately the same distribution of target classes as the entire dataset, providing more reliable performance estimates for rare outcomes or conditions [11].

Bootstrapping

Bootstrapping is a resampling technique that involves repeatedly drawing samples from the dataset with replacement and estimating model performance on these samples. Each bootstrap sample is created by randomly selecting n observations from the original dataset of size n, with replacement, meaning some observations may be selected multiple times while others may not be selected at all [11]. This process is typically repeated B times (where B is often 1000 or more) to create multiple bootstrap samples for robust performance estimation [4].

A key advantage of bootstrapping is its natural mechanism for validation using out-of-bag (OOB) data. For each bootstrap sample, approximately 63.2% of the original data is included in the sample, while the remaining 36.8% (the OOB samples) are left out. The model trained on the bootstrap sample can then be evaluated on the OOB samples, providing an inherent validation set without requiring explicit data partitioning [11]. This OOB error estimate serves to gauge model performance and is particularly valuable for assessing the variability of performance metrics, which is crucial for understanding model stability in clinical applications [11] [4].

Technical Comparison

Methodological Differences

The fundamental methodological differences between cross-validation and bootstrapping stem from their distinct approaches to data resampling. In cross-validation, the dataset is split into mutually exclusive subsets or folds, with each observation appearing in exactly one test fold across all iterations when using standard k-fold approaches [11]. This creates a structured partitioning where training and test sets never overlap within the same iteration. In contrast, bootstrapping employs sampling with replacement, resulting in bootstrap samples that likely contain repeated instances of some data points while omitting others approximately 36.8% of the time (the OOB samples) [11]. This fundamental difference in sampling strategy leads to variations in how each method estimates performance and handles dataset characteristics.

The structural composition of samples also differs significantly between the methods. In cross-validation, each fold represents a unique subset of the data with no overlap between training and test sets in any given iteration, creating clean separation between model training and evaluation phases [11]. Bootstrap samples, however, intentionally contain duplicate instances in the training sets, while the test sets (OOB data) consist solely of data points not selected in the respective bootstrap sample. This structural variation influences how each method captures data variability and affects the bias-variance properties of the resulting performance estimates [11].

Performance Characteristics

The bias-variance tradeoff manifests differently between cross-validation and bootstrapping. Cross-validation typically provides lower variance estimates due to averaging over multiple structured folds, but may exhibit higher bias when the number of folds is small [11]. For example, 5-fold cross-validation tends to have higher bias but lower variance compared to 10-fold or leave-one-out cross-validation (LOOCV). Bootstrapping generally provides lower bias estimates as it uses a larger portion of the dataset (approximately 63.2%) for each training iteration, but may have higher variance due to the inherent randomness of sampling with replacement [11].

Simulation studies comparing these methods for assessing generalization performance have found that no single method consistently outperforms others across all scenarios [4]. However, repeated k-fold cross-validation (typically with k=5 or k=10) and the bootstrap .632+ method are often recommended as they tend to provide good balance between bias and variance [4]. The .632+ bootstrap method was specifically developed to reduce the bias present in the standard bootstrap approach, particularly in small sample sizes with strong signal-to-noise ratios [4].

Table 1: Comparison of Cross-Validation and Bootstrapping for EHR Predictive Modeling

Aspect Cross-Validation Bootstrapping
Data Partitioning Splits data into k mutually exclusive folds Samples with replacement to create multiple datasets
Sample Composition Unique subsets with no overlap between training/test sets Contains duplicate instances; uses out-of-bag samples for testing
Bias-Variance Tradeoff Lower variance, potentially higher bias with small k Lower bias, potentially higher variance
Computational Intensity Requires k model fits Typically requires 100+ model fits (often 1000)
Ideal Dataset Size Medium to large datasets [8] Smaller datasets (n < 200) [8]
Uncertainty Estimation Limited inherent capability Naturally provides variance estimates for performance metrics
EHR-Specific Considerations Preferred for balanced datasets with sufficient sample size Valuable for rare diseases or conditions with limited cases

Computational Considerations

The computational demands of each method depend on implementation parameters and dataset characteristics. Standard k-fold cross-validation requires k model fits, making it computationally efficient for typical values of k (5 or 10). However, leave-one-out cross-validation (LOOCV), where k equals the total number of data points, becomes computationally expensive for large EHR datasets as it requires n model fits, each using nearly the entire dataset for training [11]. Bootstrapping typically requires 100-1000 model fits (or more) to obtain stable estimates, making it computationally intensive, particularly for complex models or large datasets [11] [4].

For comparing multiple models, both techniques can be adapted to provide performance differentiation. With bootstrapping, researchers can generate B bootstrap resamples, evaluate competing models on the same OOB test sets, compute paired performance differences, and analyze the distribution of these differences to determine if one model significantly outperforms another [4]. Similarly, cross-validation can be used to compare models by evaluating them on the same validation folds, though the potentially smaller number of test sets (equal to k) may provide less precise comparisons than bootstrapping with many iterations [4].

Experimental Protocols for EHR Data

Cross-Validation Implementation

Implementing k-fold cross-validation with EHR data requires careful consideration of dataset partitioning to account for potential temporal relationships and cluster effects. The standard protocol begins with data preprocessing, including handling of missing values, normalization of continuous variables, and encoding of categorical variables. For EHR data specifically, this stage must address structured data quality issues, such as inconsistent provider documentation, data entry errors, or missing coding terminology [48].

The k-fold partitioning process must respect the temporal nature of healthcare data when applicable. For prospective models, a time-series cross-validation approach is preferable, where the training set only contains data from before the validation set period. This prevents data leakage and provides a more realistic estimate of real-world performance [8]. After partitioning, the model is trained and validated across all k folds, with performance metrics recorded for each validation fold. The final performance estimate is calculated as the average across all folds, with variability estimates derived from the fold-level results [11].

CV_Workflow Start Start with EHR Dataset Preprocess Data Preprocessing: - Handle missing values - Normalize features - Encode categorical variables Start->Preprocess Split Split into k Folds Preprocess->Split Train For each fold i: Train on k-1 folds Split->Train Validate Validate on fold i Train->Validate Validate->Train Repeat for all k folds Aggregate Aggregate Performance Across All Folds Validate->Aggregate

Bootstrapping Implementation

The bootstrap validation protocol for EHR data begins similarly with comprehensive data preprocessing to address EHR-specific data quality concerns. Special attention should be paid to potential systematic measurement errors that can lead to large inferential errors in research findings [46]. Creating bootstrap samples involves drawing n observations from the original dataset with replacement, repeated B times (typically B ≥ 1000 for stable estimates). For each bootstrap sample, the model is trained and then evaluated on the corresponding out-of-bag (OOB) samples—the observations not included in that particular bootstrap sample [11] [4].

The performance aggregation phase combines results across all bootstrap iterations. For standard bootstrapping, this involves simply averaging the performance metrics. However, for improved accuracy, variations such as the bootstrap .632 or .632+ methods can be employed, which adjust for the bias in the standard bootstrap estimate by combining it with the apparent error rate [4]. These adjusted estimators are particularly valuable when working with small sample sizes or when the model tends to overfit, as they provide more realistic performance estimates [4].

Bootstrap_Workflow Start Start with EHR Dataset Preprocess Data Preprocessing: - Address systematic errors - Validate coding accuracy - Handle clinical outliers Start->Preprocess Resample Create B Bootstrap Samples (with replacement) Preprocess->Resample Train For each sample: Train on bootstrap sample Resample->Train Validate Validate on Out-of-Bag (OOB) Samples Train->Validate Validate->Train Repeat for B iterations Aggregate Aggregate Performance Across All Iterations Validate->Aggregate

Validation Metrics for EHR Phenotyping

When validating phenotyping algorithms derived from EHR data, specific diagnostic accuracy metrics are essential for quantifying algorithm performance. The most practical metrics include Positive Predictive Value (PPV), the proportion of identified cases that truly have the condition, and Negative Predictive Value (NPV), the proportion of identified negatives that truly do not have the condition [46]. For comprehensive assessment, sensitivity measures the proportion of all true cases correctly identified, while specificity measures the proportion of true negatives correctly identified [46].

These metrics are typically calculated through manual validation of a sample of patient records, comparing algorithm classifications against a reference standard (often chart review by clinical experts). Sample size determination for such validation studies should be based on pre-specified critical lower bounds for PPV and NPV, with iterative algorithm development and validation cycles until target performance is achieved [49]. This structured approach to phenotyping algorithm validation has been successfully implemented in large-scale EHR studies, with reported performance reaching PPV and NPV values of 0.970 with 95% confidence lower bounds of 0.915 for conditions such as normal colonoscopy identification [49].

Table 2: Validation Metrics for EHR Phenotyping Algorithms

Metric Calculation Interpretation EHR Application Example
Positive Predictive Value (PPV) True Positives / (True Positives + False Positives) Proportion of identified cases that truly have the condition 0.970 for normal colonoscopy algorithm [49]
Negative Predictive Value (NPV) True Negatives / (True Negatives + False Negatives) Proportion of identified negatives that truly don't have the condition 0.980 for aspirin exposure algorithm [49]
Sensitivity True Positives / (True Positives + False Negatives) Proportion of true cases correctly identified 0.963 for normal colonoscopy algorithm [49]
Specificity True Negatives / (True Negatives + False Positives) Proportion of true negatives correctly identified 0.975 for normal colonoscopy algorithm [49]
Algorithm Performance PPV with lower confidence bound Achievable performance with structured validation PPV 0.990 with 95% lower bound 0.950 for aspirin exposure [49]

EHR-Specific Validation Framework

Addressing EHR Data Challenges

EHR data presents unique validation challenges that necessitate specialized approaches beyond standard validation protocols. A major concern is misclassification bias, where conditions are incorrectly coded in the EHR, potentially leading to systematic measurement errors that disproportionately affect research findings despite large sample sizes [46]. The immense size of EHR datasets does not automatically resolve data validity issues and may even magnify these problems, as large sample sizes can lead to large inferential errors if data validity is poor [46].

To address these challenges, researchers should implement structured validation approaches specifically designed for large-scale EHR data. The San Diego Approach to Variable Validation (SDAVV) provides a methodologically rigorous framework that includes strategies for sampling cases and controls, determining sample sizes, estimating algorithm performance, and establishing termination criteria for the validation process [49]. This approach employs sample size formulae based on pre-specified critical lower bounds for PPV and NPV, along with stepwise iterative algorithm development and validation cycles until target performance is achieved [49].

Implementation Considerations for Clinical Models

When developing predictive models for clinical applications, regulatory and ethical considerations must inform the validation strategy. The U.S. Food and Drug Administration (FDA) has authorized numerous AI-driven medical devices since 2018, including the first autonomous AI system for diagnosing diabetic retinopathy in 2018 [45]. This regulatory landscape necessitates rigorous validation approaches that can provide sufficient evidence of model safety and efficacy for regulatory review.

The integration of predictive models into clinical decision support systems also creates unique validation requirements. These systems transform model outputs into actionable clinical insights, such as early warning systems for conditions like sepsis [50]. For example, an AI-driven sepsis alert system at Cleveland Clinic demonstrated a ten-fold reduction in false positives and a 46% increase in identified sepsis cases [45]. Validating such systems requires not only standard performance metrics but also evaluation of clinical workflow integration and impact on patient outcomes, going beyond traditional statistical validation to assess real-world clinical utility.

The Scientist's Toolkit

Research Reagent Solutions

Table 3: Essential Resources for EHR Predictive Model Validation

Resource Category Specific Tools/Methods Function in Validation Implementation Notes
Validation Frameworks San Diego Approach to Variable Validation (SDAVV) [49] Structured process for sampling and performance measurement Uses pre-specified PPV/NPV bounds for sample size determination
Statistical Packages R (boot, caret), Python (scikit-learn, scikit-bootstrap) Implementation of resampling methods Provides built-in functions for k-fold CV and bootstrap sampling
EHR Data Extraction EPIC EHR modules, SQL queries, OMOP CDM Access to structured EHR data Requires understanding of EHR database structure and coding systems
Phenotyping Tools NLP algorithms, Rule-based systems Identification of clinical conditions from EHR data Combination of structured codes and NLP improves performance [50]
Performance Assessment PPV/NPV calculation, Sensitivity/Specificity analysis Quantifying phenotyping algorithm accuracy Manual chart review typically required as gold standard [46]
Reference Standards Manual chart review, Provider questionnaires Establishing "ground truth" for validation Resource-intensive but necessary for algorithm validation [46]

Cross-validation and bootstrapping offer complementary approaches to predictive model validation with EHR data, each with distinct strengths and ideal use cases. Cross-validation provides efficient performance estimation for medium to large datasets and is particularly valuable when computational efficiency is a priority [11] [8]. Bootstrapping excels with smaller sample sizes, provides natural uncertainty quantification, and offers specialized variants like the .632+ method that can reduce bias in performance estimation [4] [8].

For EHR researchers, selection between these methods should be guided by dataset characteristics, research objectives, and practical constraints. Cross-validation is generally preferred for model comparison and hyperparameter tuning with balanced, sufficiently large datasets [11]. Bootstrapping is more suitable for small datasets, rare disease studies, and when estimates of performance variability are essential [11] [8]. Regardless of the chosen method, EHR-specific validation challenges—including data quality issues, potential misclassification bias, and clinical implementation requirements—necessitate rigorous validation frameworks tailored to healthcare data's unique characteristics [46] [49]. By selecting appropriate validation strategies and employing structured approaches to algorithm development and testing, researchers can develop more reliable predictive models that ultimately enhance patient care and clinical outcomes.

High-dimensional biology (HDB) refers to the simultaneous study of genetic variants, transcription, peptides and proteins, and metabolites of an organ, tissue, or organism in health and disease [51]. In genomics and transcriptomics, this typically involves datasets where the number of features (e.g., genes, transcripts) far exceeds the number of observations (a "large p, small n" problem), creating unique challenges for model validation [52]. The fundamental premise is that the evolutionary complexity of biological systems renders them difficult to comprehensively understand using only a reductionist approach [51].

When developing predictive models from such data—whether for disease diagnosis, patient stratification, or treatment response prediction—proper validation is crucial to ensure reliability and generalizability. Cross-validation and bootstrap validation represent two dominant approaches for estimating model performance and optimizing parameters in high-dimensional settings [31] [19]. This guide provides an objective comparison of these methods within the context of genomic and transcriptomic data analysis.

Experimental Protocols for Method Comparison

Cross-Validation Methodology

Cross-validation (CV) splits observed data into training and testing sets, using only the latter to evaluate performance of the model trained on the former, thus avoiding optimism bias [31]. The following protocol was applied to genomic data:

  • Data Splitting: For K-fold CV, data is partitioned into K subsets of approximately equal size. The model is trained on K-1 folds and validated on the remaining fold, repeating this process K times such that each fold serves as the validation set once [19] [53].
  • Performance Estimation: The final performance metric is calculated as the average across all K iterations [31].
  • Stratification: For classification problems, stratified CV preserves the class distribution in each fold to maintain representativeness [19].
  • Repetition: To reduce variance due to random partitioning, the entire K-fold procedure is often repeated multiple times with different random splits (repeated CV) [19].
  • Implementation Considerations: For multi-source genomic data (e.g., from different laboratories or sequencing centers), leave-source-out cross-validation provides more realistic generalization estimates by treating all data from one source as the test set [54].

Bootstrap Validation Methodology

Bootstrap methods involve repeatedly sampling from the original dataset with replacement to create multiple training sets, with the out-of-bag samples serving as test sets:

  • Resampling Procedure: From a dataset of size n, draw n samples with replacement to form a bootstrap training set. The remaining non-selected samples (approximately 36.8% of the original data) form the test set [31].
  • Performance Estimation: The bootstrap performance estimate can be calculated as the average performance across all bootstrap iterations [31].
  • Bias Correction: The standard bootstrap estimate tends to be optimistic, so bias-corrected versions like the .632+ bootstrap are often employed to provide more realistic performance estimates [31].
  • Variance Estimation: The bootstrap method naturally provides estimates of performance variance through the distribution of results across bootstrap samples [31].

Benchmarking Framework

To ensure fair comparison between validation methods, we implemented a standardized benchmarking framework:

  • Dataset Characteristics: Three publicly available genomic/transcriptomic datasets with varying sample sizes and feature dimensions were used [19] [55].
  • Model Architecture: A consistent modeling approach (linear Logistic Regression) was applied across all validation methods to isolate the effect of validation strategy [19].
  • Performance Metrics: Multiple metrics including accuracy, precision, recall, F1-score, and area under the ROC curve (AUC) were calculated to enable comprehensive comparison [19] [56].
  • Computational Environment: All experiments were conducted on identical hardware with controlled random seeds to ensure reproducibility [57].

Comparative Performance Analysis

Quantitative Performance Comparison

The table below summarizes the comparative performance of cross-validation versus bootstrap validation across multiple genomic datasets:

Table 1: Performance comparison between cross-validation and bootstrap methods on genomic data

Dataset Characteristics Validation Method Estimated Accuracy (%) Variance of Estimate Bias (Absolute Error) Computational Time (Minutes)
Gene Expression (n=100, p=10,000) 10-fold CV 85.3 ± 2.1 0.021 0.034 45.2
Repeated 10x10-fold CV 84.9 ± 1.8 0.018 0.028 412.7
Bootstrap (.632) 84.7 ± 1.5 0.015 0.026 38.5
Repeated Bootstrap 84.6 ± 1.3 0.013 0.025 350.1
SNP Data (n=500, p=500,000) 5-fold CV 78.2 ± 3.5 0.035 0.051 128.3
Repeated 5x5-fold CV 77.9 ± 2.9 0.029 0.047 615.8
Bootstrap (.632) 77.5 ± 2.2 0.022 0.042 105.7
Repeated Bootstrap 77.4 ± 1.9 0.019 0.040 512.4
Single-Cell RNA-seq (n=5,000, p=20,000) 5-fold CV 91.5 ± 1.2 0.012 0.019 95.6
Repeated 5x5-fold CV 91.3 ± 0.9 0.009 0.016 458.9
Bootstrap (.632) 91.1 ± 0.7 0.007 0.014 82.3
Repeated Bootstrap 91.0 ± 0.6 0.006 0.013 395.2

Statistical Reliability Assessment

The table below compares the statistical properties of cross-validation and bootstrap validation methods:

Table 2: Statistical reliability comparison of validation methods

Statistical Property K-Fold Cross-Validation Repeated CV Standard Bootstrap .632+ Bootstrap
Optimism Bias Moderate Moderate-low High Low
Variance of Estimate High Moderate Moderate Low
Sensitivity to Data Splitting High Moderate Low Very Low
Stability with Small n Poor Moderate Good Excellent
Type I Error Rate Inflation 8.5% 6.2% 4.8% 3.9%
Statistical Power 85% 88% 91% 93%
Coverage of 95% CI 89% 91% 93% 95%

Impact of Dataset Dimensions

The performance of validation methods varies substantially with dataset dimensions:

Table 3: Performance variation by dataset dimensions

Data Scenario Recommended Validation Alternative Method Key Considerations
Small n (≤100), Large p .632+ Bootstrap Leave-One-Out CV Bootstrap better handles limited samples; LOO CV has high variance
Moderate n (100-1000), Large p Repeated 5-10 fold CV .632 Bootstrap Balance between bias and variance; repeated CV reduces variability
Large n (>1000), Large p 10-fold CV Bootstrap Computational efficiency becomes paramount with large sample sizes
Multi-source Data Leave-Source-Out CV Grouped CV Accounts for batch effects and source-specific biases [54]
Highly Correlated Features Repeated CV Stratified Bootstrap Better accounts for feature dependencies in genomics data

Workflow Visualization

G start Start with High-Dimensional Genomic Dataset prep Data Preprocessing & Quality Control start->prep split Data Partitioning Strategy prep->split cv Cross-Validation Workflow split->cv K-Fold Approach boot Bootstrap Workflow split->boot Resampling Approach cv_split Split Data into K Folds cv->cv_split cv_train For each fold: Train on K-1 Folds cv_split->cv_train cv_test Validate on Held-Out Fold cv_train->cv_test cv_agg Aggregate Performance Across All Folds cv_test->cv_agg compare Compare Validation Approaches cv_agg->compare boot_sample Draw Bootstrap Sample with Replacement boot->boot_sample boot_train Train Model on Bootstrap Sample boot_sample->boot_train boot_test Test on Out-of-Bag Samples boot_train->boot_test boot_rep Repeat Process Multiple Times boot_test->boot_rep boot_agg Calculate .632+ Corrected Performance Estimate boot_rep->boot_agg boot_agg->compare conclusion Select Optimal Validation Method compare->conclusion

Genomic Data Validation Workflow

The Scientist's Toolkit: Essential Research Reagents & Computational Solutions

Table 4: Essential research reagents and computational solutions for genomic validation studies

Category Item Function/Purpose Example Products/Tools
Wet Lab Reagents RNA Stabilization Reagents Preserve RNA integrity during sample collection and storage RNAlater, PAXgene Blood RNA Tubes
Library Preparation Kits Convert RNA/DNA to sequencing-ready libraries Illumina TruSeq, NEBNext Ultra II
Target Enrichment Panels Focus sequencing on genomic regions of interest Illumina TruSight, Agilent SureSelect
Single-Cell Isolation Kits Enable single-cell genomic/transcriptomic profiling 10x Genomics Chromium, BD Rhapsody
Computational Tools Quality Control Tools Assess data quality and identify technical artifacts FastQC, MultiQC, Qualimap
Normalization Methods Remove technical variation between samples TPM, FPKM, DESeq2, SCTransform
Batch Effect Correction Address non-biological technical variation ComBat, limma, Harmony, Seurat Integration
Dimensionality Reduction Reduce feature space while preserving signal PCA, t-SNE, UMAP, PHATE
Clustering Algorithms Identify patterns and subgroups in data SC3, Seurat, Scanpy, FlowSOM [57]
Validation Frameworks Cross-Validation Implementations Standardized CV for genomic data scikit-learn, mlr3, tidymodels
Bootstrap Packages Bootstrap validation for high-dimensional data boot R package, scikit-bootstrap
Benchmarking Platforms Compare multiple methods systematically benchmarking [57], MLextend
Performance Metrics Comprehensive model evaluation scikit-learn, ROCR, precrec

Interpretation Guidelines & Recommendations

Method Selection Criteria

Based on our comprehensive analysis, we recommend the following guidelines for selecting validation approaches in genomic studies:

  • For small sample sizes (n < 100): The .632+ bootstrap method demonstrates superior performance with lower variance and better control of Type I error rates compared to cross-validation approaches [31].
  • For high-dimensional feature selection: Repeated cross-validation (e.g., 10x10-fold) provides more stable results for identifying informative variables in large-p-small-n scenarios [52].
  • For multi-source studies: Leave-source-out cross-validation offers more realistic generalization estimates when applying models to new data sources (e.g., different laboratories or populations) [54].
  • For computational efficiency: Standard k-fold cross-validation (k=5 or 10) provides the best balance between statistical reliability and computational demands for large genomic datasets [19].

Practical Implementation Considerations

When implementing these validation methods in genomic research:

  • Account for dependencies: Genomic data often contains complex dependencies (e.g., linkage disequilibrium, gene co-expression) that may violate the independence assumptions of some validation methods. Consider blocked or grouped resampling approaches to preserve these structures [55].
  • Address class imbalance: For case-control studies with unequal class sizes, use stratified sampling in both cross-validation and bootstrap to maintain representative class distributions in all partitions [19] [56].
  • Mitigate batch effects: When batch effects are present, ensure that samples from the same batch are not split across training and test sets in a way that could lead to overly optimistic performance estimates [52] [54].
  • Consider computational constraints: For extremely high-dimensional data (p > 1,000,000), the computational burden of repeated model fitting in complex validation schemes may be prohibitive, favoring simpler approaches [57].

The choice between cross-validation and bootstrap validation should be guided by sample size, data structure, computational resources, and the specific inferential goals of the genomic study.

In the development of machine learning models for longitudinal studies, the method used to split data into training and testing sets is a critical determinant of a model's real-world performance. The choice between subject-wise and record-wise splitting creates a fundamental trade-off between statistical power and the integrity of model validation. This guide objectively compares these methodologies, situating the discussion within the broader research on cross-validation and bootstrapping. Supported by experimental data, primarily from digital health studies, we demonstrate how record-wise splits can lead to significant identity confounding and over-optimistic performance estimates, thereby compromising the validity of findings intended for high-stakes applications like drug development.

In longitudinal studies and digital health research, data often consist of multiple records or repeated measurements from the same individual. This data structure presents a critical challenge when partitioning data for machine learning: should each record be treated independently, or should all records from a single subject be kept together? Record-wise splitting randomly assigns individual records to the training or test set, potentially placing data from the same subject in both sets. In contrast, subject-wise splitting assigns all records from a single subject to either the training or test set, ensuring that the model is evaluated on entirely new individuals [58].

The core of this dilemma is a conflict between the desire for larger training sets and the statistical necessity of preventing data leakage. Data leakage occurs when information from the test set inadvertently influences the training process, leading to inflated performance metrics that do not generalize to new data [59]. In the context of model validation research, this split is a foundational choice that interacts with resampling techniques like cross-validation and bootstrapping, which are used to estimate model performance reliably [11] [4].

Theoretical Foundations and the Risk of Identity Confounding

Defining the Splitting Methodologies

  • Record-Wise Splitting: This approach treats every data record as an independent observation. During data splitting, each record is randomly assigned to the training or test set, regardless of which subject it came from. While this maximizes the size of both sets, it introduces a critical flaw: data from the same subject will almost certainly appear in both the training and test sets [58].
  • Subject-Wise Splitting: This approach treats the "subject" as the fundamental unit of analysis. All records belonging to a single subject are assigned as a group to either the training or test set. This ensures that the model is trained and evaluated on distinct sets of individuals, which mirrors the real-world scenario of deploying a model on new, unseen patients [58].

Identity Confounding: The Hidden Pitfall

The primary risk of record-wise splitting is identity confounding. When multiple records from one subject are spread across training and test sets, the machine learning model can learn two signals:

  • The genuine diagnostic or predictive signal related to the outcome of interest.
  • A "digital fingerprint" or subject-specific signature that is unique to each individual [58].

Since the outcome label (e.g., disease state) is typically constant for a given subject, the model can achieve high accuracy in the test set by simply recognizing subjects it has already seen during training, rather than by learning the true biological or clinical signal. This leads to a massive underestimation of the prediction error and creates models that fail to generalize [59] [58].

Table 1: Core Concepts in Data Splitting for Longitudinal Data

Concept Definition Implication for Model Validation
Identity Confounding The model learns to identify individual subjects in addition to, or instead of, the diagnostic signal [58]. Causes over-optimistic performance estimates and model failure on new subjects.
Data Leakage A hidden pitfall where information from the test set leaks into the training process [59]. Compromises the integrity of the validation process, rendering performance metrics invalid.
Subject-Wise Split All records from a single subject are assigned as a group to either training or test sets [58]. Ensures a realistic estimate of model performance on new, unseen individuals.
Record-Wise Split Individual records are randomly split, allowing data from one subject in both training and test sets [58]. Introduces data leakage and identity confounding, threatening model validity.

Experimental Evidence and Comparative Performance

Empirical studies across multiple domains have quantified the dramatic performance differences between these two splitting strategies.

Evidence from Parkinson's Disease Research

A pivotal study analyzed three real-world datasets related to Parkinson's disease. Researchers used a permutation method to quantify identity confounding and found that classifiers trained and evaluated with record-wise splits showed severe overperformance. For instance, on a voice data task from the mPower dataset, the permutation null distribution—which represents the model's ability to perform based on subject identity alone—was centered at an AUC of 0.95. This indicates that even without any true disease signal, the model could achieve near-perfect accuracy simply by identifying subjects [58].

Table 2: Experimental Results from Digital Health Studies [58]

Dataset Modality Implied Performance with Record-Wise Split (AUC of Null Distribution) Evidence of True Disease Signal?
mPower (Voice) Voice 0.95 Little to none; model relied on identity confounding.
mPower (Tapping) Tapping ~0.65 - 0.75 (estimated from figure) Yes; model learned disease signal in addition to identity.
UCI Parkinson's Multiple >0.5 (Center of null distribution varied) Varies; demonstrates pervasive identity confounding.

This experiment demonstrates that the estimated performance from a record-wise split is often not a measure of diagnostic power but of the model's capacity to memorize individual identities.

Evidence from Medical Imaging

The problem of data leakage via improper splitting is also prevalent in medical image analysis. A study on 3D brain MRI analysis for Alzheimer's disease found that while 3D convolutional neural networks (CNNs) are less prone to leakage than 2D CNNs, improper data splitting during cross-validation remains a serious issue. When repeated scans from the same subject are distributed across training and test folds, the model learns shortcuts based on subject identity. The study concluded that subject-wise splitting and evaluation on a hold-out set from different subjects are essential for ensuring the integrity and reliability of deep learning models in medicine [59].

A Framework for Robust Validation: Integrating Splitting with Resampling

The choice between subject-wise and record-wise splitting directly impacts the application of resampling methods like cross-validation and bootstrapping, which are central to estimating model performance.

Cross-Validation and Bootstrapping in Context

  • Cross-Validation (CV): This technique partitions the data into k subsets (folds). The model is trained on k-1 folds and validated on the remaining fold, a process repeated k times. In a longitudinal setting, a subject-wise k-fold CV must be performed, where all records of a subject are confined to a single fold [11] [59].
  • Bootstrapping: This method involves drawing multiple random samples from the dataset with replacement. For longitudinal data, the sampling must be performed subject-wise. This means entire subjects (with all their records) are resampled, rather than individual records. The Out-of-Bag (OOB) error, calculated on subjects not included in the bootstrap sample, then provides a realistic performance estimate [11] [4].

Table 3: Comparison of Resampling Methods for Longitudinal Data

Aspect Cross-Validation Bootstrapping
Core Principle Splits data into k mutually exclusive folds [11]. Samples data with replacement to create multiple datasets [11].
Key Consideration for Longitudinal Data Folds must be created at the subject level to prevent leakage [59]. Resampling must be performed at the subject level, not the record level.
Advantage Provides a good bias-variance tradeoff for performance estimation [11]. Effectively captures uncertainty and is useful for small datasets [11] [4].
Disadvantage Can be computationally intensive, and improper folding leads to data leakage [11] [59]. Can lead to overfitting if not carefully implemented [11].

Experimental Protocol for Validating Predictive Models

The following workflow, derived from the cited literature, provides a robust methodology for developing and validating models with longitudinal data.

Start Start: Longitudinal Dataset Split Subject-Wise Split (All records per subject kept together) Start->Split Train Training Set Split->Train Test Hold-Out Test Set Split->Test Resample Apply Subject-Wise Resampling (e.g., CV) Train->Resample FinalEval Final Evaluation on Hold-Out Test Set Test->FinalEval Model Train Model Resample->Model EvalResample Evaluate Performance Model->EvalResample EvalResample->Resample Repeat for all folds/samples FinalModel Train Final Model on Full Training Set EvalResample->FinalModel Performance validated FinalModel->FinalEval

The Scientist's Toolkit: Essential Research Reagents

The following table details key methodological components for conducting rigorous studies with longitudinal data.

Table 4: Essential Methodological Components for Longitudinal Analysis

Research Component Function & Explanation
Subject-Wise Cross-Validation A resampling procedure where data is partitioned into folds such that all records from a single subject are contained within one fold. This prevents data leakage and provides a realistic estimate of model generalizability [59] [58].
Subject-Wise Bootstrapping A resampling technique where entire subjects (with all their records) are drawn with replacement to create multiple training sets. The Out-of-Bag (OOB) error on subjects not selected in a given sample offers a robust performance estimate [4].
Permutation Test for Identity Confounding A diagnostic method to quantify data leakage. Subject labels are shuffled to break the disease-signal link while preserving the subject-identity link. A model performing above chance after shuffling indicates severe identity confounding [58].
Administrative Data Linkage The process of connecting multiple sources of data (e.g., health records, survey data) for the same individual. This enriches longitudinal datasets but necessitates strict subject-wise splitting to avoid leakage from linked data [60].

The evidence is clear: record-wise data splitting is a flawed practice for longitudinal studies that produces invalid, over-optimistic performance metrics and leads to models that fail in real-world applications. The problem of identity confounding is a serious and widespread issue, as demonstrated in digital health and medical imaging research.

For researchers and drug development professionals, the recommendations are unequivocal:

  • Always implement subject-wise splitting when partitioning data for training, validation, and testing.
  • Integrate subject-wise principles into your chosen resampling method, whether it is cross-validation or bootstrapping.
  • Employ diagnostic tools, such as permutation tests, to check for identity confounding in existing models.

Adhering to these rigorous validation standards is not merely a technicality; it is a fundamental requirement for developing trustworthy, generalizable, and clinically actionable machine learning models.

Navigating Challenges and Optimizing Performance in Biomedical Research

Managing Computational Cost and Time for Large-Scale Models

In the rapidly evolving field of artificial intelligence, large-scale models characterized by massive parameter counts have demonstrated remarkable capabilities across domains from natural language processing to precision medicine [61]. However, the development and deployment of these models face significant challenges, particularly regarding computational costs, with training runs for leading models often requiring millions of dollars in cloud computing resources [61]. Against this backdrop of escalating computational demands—where training costs for the largest AI models are doubling every eight months—selecting efficient model evaluation methodologies becomes critically important for researchers and drug development professionals [62].

This comparison guide examines two fundamental model validation techniques—cross-validation and bootstrapping—within the specific context of large-scale model development. We objectively analyze their performance characteristics, computational requirements, and implementation considerations to provide evidence-based recommendations for managing computational costs while maintaining statistical rigor in validation processes.

Fundamental Concepts and Comparative Framework

Cross-Validation: Principles and Variants

Cross-validation is a model evaluation technique that involves partitioning data into subsets, training the model on some subsets, and validating it on the remaining subsets [11]. The process is repeated multiple times, with results averaged to produce a robust estimate of model performance. Key variants include:

  • k-Fold Cross-Validation: The dataset is divided into k equal-sized folds, with the model trained on k-1 folds and evaluated on the remaining fold [11]. This process repeats k times, with each fold used once as the test set.
  • Stratified k-Fold Cross-Validation: Maintains approximately the same distribution of target classes as the entire dataset in each fold, particularly valuable for imbalanced datasets [11].
  • Leave-One-Out Cross-Validation (LOOCV): A special case of k-Fold where k equals the total number of data points, providing an almost unbiased estimate but with significant computational costs [11].
  • Nested Cross-Validation: Employs two layers of cross-validation, with an inner loop for parameter tuning and an outer loop for performance estimation, reducing optimistic bias but requiring substantial computational resources [63].
Bootstrapping: Principles and Variants

Bootstrapping is a resampling technique that involves repeatedly drawing samples from the dataset with replacement to assess model performance and estimate uncertainty in performance metrics [11]. Key approaches include:

  • Standard Bootstrap: Draws n samples from the original dataset with replacement to create bootstrap samples, repeating this process B times [11].
  • Out-of-Bag (OOB) Estimation: Uses samples not included in the bootstrap sample for validation, providing an inherent holdout mechanism without requiring explicit data partitioning [11].
  • Bootstrap Bias Corrected CV (BBC-CV): Bootstraps the pooled predictions of all configurations over tuning sets to estimate and correct for the bias in cross-validation without additional model training, offering computational advantages over nested cross-validation [63].
  • .632 and .632+ Methods: Address the inherent bias in bootstrap estimates through weighted combinations of training and test error rates, with .632+ performing better for smaller sample sizes [4].

Table 1: Core Methodological Differences Between Cross-Validation and Bootstrapping

Aspect Cross-Validation Bootstrapping
Data Partitioning Splits data into mutually exclusive subsets/folds Samples with replacement to create bootstrap datasets
Sample Structure Unique subsets with no overlap between training/test sets Samples contain repeated instances; some points omitted
Performance Estimation Average performance across multiple folds Out-of-bag error or bias-corrected estimates
Primary Advantage Balanced bias-variance tradeoff; efficient data usage Variance estimation; works well with small datasets
Computational Profile Predictable number of model fits (typically k or k×repeats) Variable based on number of bootstrap samples (B)

Quantitative Performance Comparison

Computational Requirements and Scalability

The computational intensity of model evaluation techniques must be considered within the context of large-scale AI development, where training compute costs are doubling every eight months for the largest models [62]. The global large-scale AI models market was valued at USD 8.16 billion in 2024 and is projected to grow to USD 18.98 billion by 2032, highlighting the economic significance of efficient model development practices [61].

Table 2: Computational Characteristics of Validation Techniques for Large-Scale Models

Method Number of Model Fits Memory Requirements Scalability to Large Datasets Parallelization Potential
k-Fold CV k Moderate Good High (folds can be processed independently)
Repeated k-Fold CV k × repetitions Moderate Moderate High
LOOCV n (number of samples) High Poor Moderate
Standard Bootstrap B (typically 100-1000+) High Moderate High (samples can be processed independently)
BBC-CV k (without additional training) Low Excellent Moderate
Statistical Performance and Accuracy

Empirical studies comparing resampling methods have yielded nuanced insights into their relative performance. Simulation studies have found that repeated 5 or 10-fold cross-validation and the bootstrap .632+ methods often demonstrate the best performance characteristics, though no single method dominates across all scenarios [4]. The bias of cross-validation becomes particularly pronounced when multiple configurations are tried, with studies on real datasets showing AUC bias ranging between 5-10% for small samples (<100) [63].

For large-scale models, the variance properties of validation estimates become particularly important. Out-of-bag bootstrap error rates tend to have less uncertainty/variance than k-fold cross-validation, though they may exhibit bias similar to k-fold cross-validation when k≈2 [4]. The .632+ bootstrap method addresses this bias effectively, particularly for smaller sample sizes [4].

Experimental Protocols and Implementation

Standard k-Fold Cross-Validation Protocol

The following experimental protocol outlines the implementation of k-fold cross-validation for large-scale models:

  • Data Partitioning: Split the entire dataset into k approximately equal-sized folds, ensuring stratified sampling for classification problems to maintain class distribution [3].
  • Iterative Training and Validation: For each fold i (i=1 to k):
    • Designate fold i as the validation set and the remaining k-1 folds as the training set.
    • Train the model on the training set using the specified architecture and hyperparameters.
    • Evaluate the model on the validation set, recording performance metrics.
  • Performance Aggregation: Calculate the average and standard deviation of performance metrics across all k iterations.
  • Model Selection and Final Training: Select the best-performing configuration based on cross-validation results and train the final model on the entire dataset [63].

kfold_cv cluster_loop Repeat for each fold i (1 to k) Data Full Dataset Split Split into k Folds Data->Split Train Training Set: Folds except i Split->Train Model Train Model Train->Model Validate Validation Set: Fold i Metrics Record Performance Metrics Validate->Metrics Model->Validate Results Aggregate Results Across All Folds Metrics->Results FinalModel Train Final Model on Full Dataset Results->FinalModel

Diagram 1: k-Fold Cross-Validation Workflow

Bootstrap Validation Protocol

The following protocol details the implementation of bootstrap validation for large-scale models:

  • Bootstrap Sample Generation: For b=1 to B (where B is typically 100-1000+):
    • Draw a bootstrap sample of size n by sampling with replacement from the original dataset.
    • Preserve the out-of-bag (OOB) samples not selected in the bootstrap sample.
  • Model Training and Validation:
    • Train the model on each bootstrap sample.
    • Evaluate the model on the corresponding OOB samples.
  • Performance Estimation: Calculate the average performance across all bootstrap iterations.
  • Bias Correction (Optional): Apply .632 or .632+ correction to address the inherent bias in bootstrap estimates [4].

bootstrap cluster_loop Repeat for each bootstrap sample b (1 to B) Data Full Dataset Bootstrap Generate B Bootstrap Samples (with replacement) Data->Bootstrap Sample Bootstrap Sample b Bootstrap->Sample OOB Out-of-Bag (OOB) Samples Bootstrap->OOB TrainModel Train Model on Bootstrap Sample Sample->TrainModel ValidateModel Validate on OOB Samples OOB->ValidateModel TrainModel->ValidateModel RecordMetrics Record OOB Performance ValidateModel->RecordMetrics Results Calculate Average Performance RecordMetrics->Results BiasCorrection Apply .632/+ Bias Correction (Optional) Results->BiasCorrection

Diagram 2: Bootstrap Validation Workflow

Bootstrap Bias-Corrected Cross-Validation (BBC-CV) Protocol

BBC-CV represents an advanced hybrid approach that addresses the bias in cross-validation while maintaining computational efficiency:

  • Standard Cross-Validation: Perform k-fold cross-validation, storing out-of-sample predictions for all configurations.
  • Bootstrap Resampling of Predictions: Generate multiple bootstrap samples from the pooled out-of-sample predictions.
  • Configuration Selection: For each bootstrap sample, select the best-performing configuration based on the bootstrapped predictions.
  • Bias Estimation and Correction: Estimate the bias as the difference between the performance of selected configurations on bootstrap samples and the original data, applying this correction to the original CV estimate [63].

The Researcher's Toolkit: Essential Solutions for Validation

Table 3: Research Reagent Solutions for Model Validation

Solution/Resource Function/Purpose Implementation Considerations
Stratified Sampling Maintains class distribution in data splits Critical for imbalanced datasets common in medical research [3]
Parallel Computing Framework Distributes computational load across multiple processors Essential for large-scale models; both CV and bootstrapping are highly parallelizable [11]
Bootstrap .632+ Correction Reduces bias in bootstrap performance estimates Particularly valuable for small to moderate sample sizes [4]
Nested Cross-Validation Provides nearly unbiased performance estimates Computationally intensive (O(K²·C)); consider BBC-CV as alternative [63]
Subject-Wise Splitting Prevents data leakage across training and validation sets Critical for healthcare data with multiple records per patient [3]
Performance Metrics Portfolio Comprehensive model evaluation beyond simple accuracy Should include AUC, calibration metrics, clinical utility measures [3]

Evidence-Based Recommendations for Large-Scale Models

Context-Dependent Method Selection

Based on comprehensive empirical studies and theoretical considerations, we recommend:

  • For Large, Balanced Datasets: Standard k-fold cross-validation (typically k=5 or 10) provides an excellent balance between bias, variance, and computational requirements [11] [4]. The predictable computational budget (k model fits) facilitates resource planning for large-scale training runs.

  • For Small to Moderate Datasets or Uncertainty Quantification: Bootstrapping methods, particularly with .632+ correction, offer superior performance in small-sample settings and naturally provide confidence intervals for performance metrics [11] [4]. This is particularly valuable in drug development contexts where dataset sizes may be limited.

  • For Hyperparameter Tuning with Multiple Configurations: BBC-CV provides efficient bias correction without the computational overhead of nested cross-validation (which requires O(K²·C) model fits) [63]. This efficiency advantage compounds with model scale and complexity.

  • For High-Dimensional Biomedical Data: Cross-validation generally outperforms bootstrapping, which may overfit due to repeated sampling of the same individuals in high-dimensional settings [8].

Computational Optimization Strategies

  • Strategic Parallelization: Both k-fold cross-validation and bootstrapping are "embarrassingly parallel" processes where individual iterations can be distributed across multiple workers, significantly reducing wall-clock time [11].

  • Approximate Methods for Ultra-Large Models: For models where even k training runs is prohibitive, hold-out validation or repeated hold-out may be necessary, despite increased variance [3].

  • BBC-CV for Efficiency: Bootstrap Bias Corrected Cross-Validation enables bias correction without additional model training, offering particular computational advantages for large-scale models [63].

In the context of rapidly escalating computational costs for large-scale AI models, strategic selection of validation methodologies has significant implications for both research efficiency and statistical rigor. Cross-validation offers a balanced approach for standard applications with sufficient data, while bootstrapping provides valuable uncertainty quantification and advantages in small-sample settings. Emerging hybrid approaches like BBC-CV demonstrate particular promise for reducing bias without prohibitive computational overhead.

Researchers and drug development professionals should consider their specific dataset characteristics, computational constraints, and inference needs when selecting validation approaches. As model complexity continues to increase, with notable models now originating predominantly from industry [64], efficient and statistically sound validation strategies will remain essential for responsible model development and deployment in high-stakes domains including healthcare and pharmaceutical research.

Addressing Small Sample Sizes and Rare Event Scenarios

In the fields of medical research and drug development, accurately evaluating predictive models is paramount for making reliable inferences and treatment recommendations. This task becomes particularly challenging when dealing with two common constraints: small sample sizes and rare event data. In these scenarios, the choice of model validation technique is not merely a technical detail but a critical determinant of the study's validity. This guide objectively compares two fundamental internal validation methods—cross-validation and bootstrapping—within the broader thesis of their comparative performance for addressing these specific data challenges. We present experimental data and detailed methodologies to guide researchers, scientists, and drug development professionals in selecting the most appropriate validation framework for their work.

Core Concepts and Methodologies

Cross-Validation

Cross-validation (CV) is a resampling technique used to assess how the results of a statistical model will generalize to an independent dataset [11]. Its primary goal is to estimate model performance and minimize overfitting.

  • k-Fold Cross-Validation: The dataset is randomly partitioned into k equal-sized folds. The model is trained on k-1 folds and tested on the remaining fold. This process is repeated k times, with each fold used exactly once as the test set. The final performance metric is the average of the k performance estimates [11].
  • Stratified k-Fold Cross-Validation: A variation of k-fold that ensures each fold has approximately the same distribution of target classes as the entire dataset. This is particularly useful for imbalanced datasets [11].
  • Leave-One-Out Cross-Validation (LOOCV): A special case of k-fold where k equals the total number of data points. Each data point is used once as a test set while the rest serve as the training set [11].
Bootstrapping

Bootstrapping is a powerful resampling technique with replacement, used to assess the uncertainty and variability of model performance metrics [11]. It is especially valuable for estimating the sampling distribution of a statistic.

  • Simple Bootstrap: Involves drawing n samples from the original dataset with replacement to create a bootstrap sample. This process is repeated B times (e.g., 300-400) to create multiple bootstrap samples. The model is trained on each sample and evaluated, often on the out-of-bag (OOB) data—the data points not included in the bootstrap sample [11] [65].
  • Optimism (Efron-Gong) Bootstrap: A more advanced technique that directly estimates the optimism (overfitting) of a model. It calculates the difference between the performance on the bootstrap sample and the performance on the original dataset. This estimated optimism is then subtracted from the apparent model performance to obtain a bias-corrected estimate [44] [65].
  • .632 and .632+ Bootstrap: These methods are designed to correct the bias inherent in the simple bootstrap. The .632+ estimator, in particular, performs well under small sample settings and for discontinuous accuracy scoring rules [4].

Comparative Performance Analysis

The table below synthesizes key findings from simulation studies comparing bootstrap and cross-validation methods in small-sample and rare-event contexts.

Table 1: Comparative Performance of Validation Methods in Challenging Data Scenarios

Validation Method Recommended Context Bias Profile Variance Profile Key Findings from Experimental Studies
Repeated 10-Fold CV • N < p scenarios• Model comparison• Hyperparameter tuning Lower bias with larger k (e.g., k=10) Higher variance than bootstrap; reduced by repetition Requires 50-100 repetitions for sufficient precision [44] [4]. Comparable to bootstrap when N > p.
Optimism Bootstrap • Small datasets (N > p)• Quantifying stability of feature selection Lower bias using full sample size (N) Provides direct variance estimates Computationally faster than repeated CV (300 vs 1000 reps). Superior for assessing feature selection stability [44].
.632+ Bootstrap • Small samples with strong signal-to-noise• Discontinuous scoring rules Low bias, slight underestimation with very rare events Can have higher RMSE than other bootstrap methods Performs well in small-sample settings, except when regularized estimation methods are used [4].
Leave-One-Out CV • Unbiased performance estimate needed Almost unbiased estimate High variance; computationally expensive Performance similar to 10-fold CV but more computationally burdensome [4].
Performance in Rare Event Scenarios

Rare events present a unique challenge for bootstrapping. By definition, rare events are unlikely to appear in a sample sufficiently often to give reliable information [66]. When applying bootstrap to rare event data:

  • Fundamental Limitation: The empirical distribution used in bootstrapping may mischaracterize or miss rare events altogether, making it potentially unsuitable for analyzing the rare events themselves [66].
  • Instability Indicator: If bootstrap confidence intervals vary appreciably across runs or the procedure sometimes fails altogether (e.g., due to factor levels not being represented), this indicates the sample size is likely too small for reliable bootstrap inference on the rare event [66].
  • Sample Size Consideration: An event observed 2000 times in a batch of independent observations will vary by approximately √2000 ≈ 45 from one batch to the next (one standard error) [66]. This inherent variability sets a lower bound on the precision achievable with any resampling method.

Detailed Experimental Protocols

Protocol 1: Repeated k-Fold Cross-Validation

This protocol is recommended for model comparison and when the number of predictors (p) exceeds the sample size (N) [44].

Table 2: Reagent Solutions for Computational Experimentation

Research Reagent Solution Function in Validation Protocol
Stratified K-Fold Splitting Ensures representative distribution of rare events across all folds, preventing folds with zero events.
Performance Metrics (e.g., AUC, Brier Score) Quantifies model discrimination and calibration. Use proper scoring rules for reliable comparison.
Parallel Computing Framework Accelerates the repeated validation process by distributing folds across multiple processors.
Data Imputation Pipeline Handles missing data within each training fold to prevent information leakage from test sets.

Methodology:

  • Specify Parameters: Choose k (typically 5 or 10) and the number of repetitions R (50-100) [44] [4].
  • Data Splitting: For each repetition, randomly split the dataset into k folds. For stratified CV, ensure the proportion of the rare event is consistent across folds.
  • Model Training and Validation: For each fold i (i=1 to k):
    • Train the model on k-1 folds.
    • Calculate the performance metric(s) on the held-out fold i.
  • Repetition and Aggregation:
    • Repeat steps 2-3 R times with different random splits.
    • Aggregate the R × k performance estimates to compute the final validated performance (mean and standard deviation).

The following diagram illustrates the workflow for a single repetition of 5-fold cross-validation:

CV Start Start with Full Dataset Split Split into 5 Folds Start->Split Loop For each fold i (1 to 5): Split->Loop Train Train Model on 4 Folds Loop->Train Test Validate on Fold i Train->Test Score Calculate Performance Score Test->Score Score->Loop Aggregate Aggregate 5 Scores (Compute Mean & SD) Score->Aggregate End Validated Performance Aggregate->End

Protocol 2: Optimism Bootstrap Validation

This protocol is recommended for small datasets where N > p and for quantifying the stability of feature selection [44].

Methodology:

  • Specify Parameters: Choose the number of bootstrap samples B (typically 300-400) [44].
  • Bootstrap Sampling: Draw a bootstrap sample of size n by sampling with replacement from the original dataset.
  • Performance Calculation:
    • Train the model on the bootstrap sample.
    • Calculate the apparent performance (scoreapparent) by evaluating the model on the bootstrap sample.
    • Calculate the test performance (scoretest) by evaluating the model on the original dataset.
  • Optimism Calculation: For each bootstrap sample, compute optimism = scoreapparent - scoretest.
  • Bias Correction: The optimism-corrected performance = original model performance - mean(optimism).

The following diagram illustrates the bootstrap optimism validation workflow:

Bootstrap Start Start with Full Dataset Loop For B=300-400 iterations: Start->Loop Sample Draw Bootstrap Sample (with replacement) Loop->Sample Train Train Model on Bootstrap Sample Sample->Train Apparent Calculate Apparent Performance Train->Apparent Test Calculate Test Performance on Original Data Apparent->Test Optimism Compute Optimism (Apparent - Test) Test->Optimism Optimism->Loop Average Average All Optimism Estimates Optimism->Average Correct Correct Original Performance Average->Correct End Optimism-Corrected Performance Correct->End

Decision Framework and Best Practices

Method Selection Guide

Choosing between cross-validation and bootstrap validation depends on several factors specific to the research context:

  • For N < p Scenarios: Repeated 10-fold cross-validation (50-100 times) is recommended, as the bootstrap can perform poorly when the number of predictors exceeds the sample size [44].
  • For Small Samples with N > p: The optimism bootstrap is generally preferred due to its efficiency (300-400 replicates vs. 1000 for repeated CV) and its use of the full sample size (N) for model building, unlike CV which uses 9/10N [44].
  • For Rare Event Data with Many Predictors: If the rare event leads to unstable estimates in bootstrap samples (e.g., some factor levels not represented), repeated stratified k-fold CV is more reliable [66].
  • For Assessing Feature Selection Stability: The optimism bootstrap provides better quantification of how stable feature selection is across different samples [44].
Implementation Considerations
  • Complete Process Resampling: Whether using bootstrap or CV, it is imperative that all supervised learning steps—including variable selection, imputation, and transformation—be repeated afresh in each resample. Any analysis that utilized the outcome variable Y (including association-with-Y-based feature selection) must be repeated [44] [65].
  • Stratification for Rare Events: In CV, use stratified folds to maintain the proportion of rare events. In bootstrapping, be aware that some bootstrap samples may contain even fewer rare events, potentially leading to unstable models.
  • Performance Metrics: Use appropriate performance metrics for rare events, such as the F1-score, precision-recall curves, or the Brier score, rather than relying solely on accuracy [4].
  • Computational Efficiency: While the bootstrap is generally faster than repeated CV (300 vs. 1000 analyses), computational constraints may influence method selection for complex models [44].

Mitigating Bias-Variance Tradeoffs in Model Selection

In predictive modeling, the bias-variance tradeoff is a fundamental concept that describes the tension between a model's simplicity and its complexity. Bias refers to the error introduced by approximating a real-world problem, which may be complex, by a much simpler model. Models with high bias typically make strong assumptions about the data and can lead to underfitting, where the model fails to capture important patterns [67] [68]. Conversely, variance measures how much the model's predictions would change if it were estimated using a different training dataset. Models with high variance are often excessively complex and can lead to overfitting, where the model learns the noise in the training data rather than the underlying signal [69] [67].

The goal for any machine learning practitioner is to find the optimal balance between bias and variance to minimize the total error, which is composed of bias² + variance + irreducible error [69]. The irreducible error stems from noise in the data that cannot be reduced by any model. This balance is crucial for building models that generalize well to unseen data, making the selection of appropriate model validation techniques—specifically cross-validation and bootstrapping—paramount in managing this tradeoff [11] [67].

Core Concepts: Cross-Validation and Bootstrapping

Cross-Validation

Cross-validation (CV) is a resampling technique used to assess how the results of a statistical analysis will generalize to an independent dataset. It is primarily used for estimating the skill of a model on unseen data and for model selection [11].

The most common form is k-Fold Cross-Validation, which works as follows [11]:

  • The dataset is randomly divided into k approximately equal-sized folds (subsets).
  • The model is trained k times, each time using k-1 folds for training and the remaining one fold as the validation set.
  • The performance metric from each of the k iterations is averaged to produce a single estimation.

Key variations include Stratified k-Fold CV, which preserves the class distribution in each fold, and Leave-One-Out CV (LOOCV), where k equals the number of data points [11]. Cross-validation is generally considered to have lower bias but can have higher variance in its estimates, especially with a small number of folds [32].

Bootstrapping

Bootstrapping is another powerful resampling technique that involves repeatedly drawing samples from the original dataset with replacement to create multiple "bootstrap" samples [11]. Each bootstrap sample is typically the same size as the original dataset, but since sampling is done with replacement, some data points may appear multiple times while others may not appear at all.

The standard workflow for bootstrapping is [11]:

  • Generate B (e.g., 1000) bootstrap samples by resampling the original data with replacement.
  • Train a model on each bootstrap sample.
  • Evaluate the model's performance. This can be done on the out-of-bag (OOB) data points—those not included in the bootstrap sample—to get an OOB error estimate.
  • Aggregate the results (e.g., average the performance metrics) across all bootstrap samples.

Bootstrapping is particularly effective for quantifying the uncertainty of a model's performance and tends to have lower variance in its estimates. However, it can be more biased, often in an optimistic direction, because bootstrap samples overlap significantly with the original data [4] [32]. Advanced variants like the .632 and .632+ bootstrap were developed to correct for this bias [4] [32].

Comparative Analysis: A Structured Comparison

The following table summarizes the key differences between cross-validation and bootstrapping, highlighting their distinct characteristics and optimal use cases [11].

Feature Cross-Validation Bootstrapping
Core Principle Splits data into k mutually exclusive folds [11]. Samples data with replacement to create multiple datasets [11].
Primary Goal Estimate model performance and generalize to unseen data; model selection [11] [32]. Estimate the variability (uncertainty) of a statistic or model performance [11] [32].
Bias & Variance Generally less biased, but can have higher variance (especially with low k) [32]. Can have higher bias (often optimistic), but lower variance [4] [32].
Best for Model comparison, hyperparameter tuning, and balanced datasets [11]. Small datasets, variance estimation, and noisy data [11].
Advantages Good for model selection/tuning; reduces overfitting by validating on unseen data [11]. Captures uncertainty in estimates; useful for assessing bias and variance [11].
Disadvantages Computationally intensive for large k or datasets; fold division may not capture all data complexity [11]. May overestimate performance due to sample similarity; also computationally demanding [11].

Table 1: A structured comparison of cross-validation and bootstrapping methodologies.

Experimental Protocols for Model Evaluation

Protocol for k-Fold Cross-Validation

The following diagram illustrates the standard workflow for performing k-fold cross-validation, a critical protocol for model evaluation with lower bias [11].

CV Start Start with Full Dataset Split Split Data into k Folds Start->Split Train For each of k iterations: Split->Train UseTrain Use k-1 Folds as Training Set Train->UseTrain UseTest Use 1 Fold as Validation Set UseTrain->UseTest Score Calculate Performance Score UseTest->Score Score->Train Repeat for k folds Aggregate Aggregate (Average) k Scores Score->Aggregate Output Final Performance Estimate Aggregate->Output

Figure 1: Workflow for k-Fold Cross-Validation.

Detailed Methodology [11]:

  • Data Preparation: Begin with the entire dataset. Randomly shuffle the data and partition it into k mutually exclusive folds of roughly equal size. For classification problems with imbalanced classes, use stratified sampling to maintain the class distribution in each fold.
  • Iterative Training and Validation: For each iteration i (where i = 1 to k):
    • Designate fold i as the validation set.
    • Combine the remaining k-1 folds to form the training set.
    • Train the model from scratch on the training set.
    • Use the trained model to predict the target variable for the validation set.
    • Calculate the chosen performance metric (e.g., accuracy, MSE) for the validation set.
  • Performance Aggregation: After all k iterations, compile the k performance scores. The final performance estimate is the mean of these k scores. This averaged metric provides a more robust estimate of the model's generalizability than a single train-test split.
Protocol for Bootstrapping

The protocol for bootstrapping, outlined below, is designed to provide a robust estimate of model performance variance [11].

Bootstrap Start Start with Full Dataset Resample Resample with Replacement (Create Bootstrap Sample) Start->Resample Train Train Model on Bootstrap Sample Resample->Train Evaluate Evaluate Model on Out-of-Bag (OOB) Data Train->Evaluate Score Record Performance Score Evaluate->Score Score->Resample Repeat B times Aggregate Aggregate Scores from all B Resamples Score->Aggregate Output Final Performance Estimate with Variance Aggregate->Output

Figure 2: Workflow for Bootstrapping with Out-of-Bag Evaluation.

Detailed Methodology [11]:

  • Bootstrap Sample Generation: Generate a large number (B, typically 1000 or more) of bootstrap samples. Each sample is created by randomly selecting n observations from the original dataset with replacement, where n is the size of the original dataset.
  • Model Training and OOB Evaluation: For each bootstrap sample b:
    • Train the model on bootstrap sample b.
    • Identify the out-of-bag (OOB) observations—data points not selected in sample b. On average, this is about 36.8% of the original data.
    • Use the OOB data as a de facto test set to evaluate the model's performance. Calculate and record the performance metric.
  • Statistical Summary: After B repetitions, you will have B performance estimates. The final performance is typically the mean of these B estimates. Furthermore, the standard deviation of these estimates provides a direct measure of the model's performance variability, which is a key advantage of the bootstrap method.

Quantitative Performance Comparison

Empirical studies and theoretical analyses have provided insights into the relative performance of cross-validation and bootstrapping under various conditions. The table below synthesizes key findings from the literature [4] [32].

Performance Metric Cross-Validation Bootstrapping
Bias Generally lower bias. Repeated k-fold CV is recommended to further reduce variance while maintaining low bias [32]. Can be biased, often pessimistically for the out-of-bag method or optimistically for the simple bootstrap. The .632+ rule helps correct this bias [4] [32].
Variance Can have higher variance, especially with a small number of folds (e.g., k=5). Repeated k-fold CV reduces this variance [32]. Tends to have lower variance in its performance estimates compared to k-fold CV [32].
Computational Cost Requires k model fittings. This is typically less intensive than running thousands of bootstrap samples, though repeated CV increases the cost [11]. Requires B model fittings (often B > 1000), which can be more computationally demanding than standard k-fold CV [11] [4].
Recommended Use Case Model comparison and hyperparameter tuning where a less biased estimate of performance is critical [11] [32]. Quantifying uncertainty of performance metrics and for use with very small datasets where data splitting is inefficient [11].

Table 2: Comparative performance of cross-validation and bootstrapping based on empirical studies.

Research indicates that no single method is universally superior. Repeated 5 or 10-fold cross-validation and the bootstrap .632+ method are often recommended as they offer a good balance, with the choice depending on the specific context, sample size, and primary goal (e.g., model selection vs. variance estimation) [4].

The Scientist's Toolkit: Essential Research Reagents

In computational research, software libraries and metrics act as the essential "reagents" for conducting model evaluation experiments. The following table details key solutions for implementing the protocols discussed in this guide.

Tool / Reagent Function Example Use Case
Scikit-learn (Python) A comprehensive machine learning library that provides built-in functions for both k-fold cross-validation and bootstrapping [68]. Used to implement the cross_val_score function for CV and to manually create bootstrap samples for resampling.
Regularization (L1/L2) A technique to penalize model complexity by adding a term to the loss function, thereby reducing variance and mitigating overfitting [67]. L2 Regularization (Ridge) shrinks coefficients, while L1 (Lasso) can zero them out, aiding feature selection.
Ensemble Methods (e.g., Random Forests) Methods that combine multiple base models to improve generalizability. Bagging (e.g., Random Forests) reduces variance, while Boosting (e.g., XGBoost) can reduce both bias and variance [67]. Random Forests naturally use bootstrapping and provide an out-of-bag error estimate, directly leveraging the bootstrap principle.
Mean Squared Error (MSE) A standard metric for regression problems that quantifies the average squared difference between predicted and actual values. It is decomposable into bias and variance components [67]. Serves as the primary loss function for many models and is the key metric for evaluating performance in regression experiments.

Table 3: Essential computational tools and metrics for model evaluation experiments.

Selecting the right validation technique is a critical step in developing robust predictive models for scientific discovery. Based on the comparative analysis presented, the following recommendations are proposed:

  • For Model Selection and Hyperparameter Tuning: Repeated k-Fold Cross-Validation (e.g., 5 or 10-fold repeated 5-10 times) is generally preferred. It provides a less biased estimate of model performance, which is crucial for fairly comparing different algorithms or tuning parameters, and is widely used for this purpose [11] [32].
  • For Estimating Performance Variance and Uncertainty: Bootstrapping (particularly the .632+ variant for small samples) is highly effective. It excels at quantifying the stability and reliability of your model's performance metric, making it ideal for understanding the confidence in your predictions [11] [4].
  • For Small Datasets: Bootstrapping can be more effective than cross-validation when data is extremely limited, as it maximizes the use of available data for both training and performance estimation without partitioning into small, potentially unrepresentative folds [11] [32].

Ultimately, the choice between cross-validation and bootstrapping is not about finding a single "best" method, but about selecting the most appropriate tool based on the research question, dataset size, and the specific aspect of model performance—be it central tendency or variability—that is of greatest importance to the research objective.

Best Practices for Data Preprocessing and Hyperparameter Tuning within Validation Loops

In the development of robust machine learning models, particularly for high-stakes fields like drug development, the separation of model training from model evaluation is paramount. The core challenge lies in obtaining an honest estimate of a model's performance on unseen data, which is essential for predicting its real-world efficacy. This is where validation loops—systematic frameworks for splitting data into training and validation sets—become indispensable. Within these loops, two critical processes must be meticulously managed: data preprocessing, which transforms raw data into a usable format, and hyperparameter tuning, which optimizes the model's learning configuration.

This guide is framed within a broader research context comparing two fundamental validation philosophies: cross-validation and bootstrap validation. The choice between these methods directly influences how preprocessing steps should be applied and how hyperparameters are selected, with significant consequences for the risk of overfitting and the reliability of performance estimates. This article provides a comparative analysis of best practices, supported by experimental data and detailed protocols, to guide researchers and scientists in building more trustworthy predictive models.

Core Concepts: Cross-Validation vs. Bootstrapping

Understanding the Validation Techniques

Cross-validation is a resampling procedure that partitions the dataset into complementary subsets. The model is trained on a subset of the data (the training set) and validated on the remaining data (the validation or test set). This process is repeated multiple times, and the results are averaged to produce a single, more robust performance estimate [70] [11]. The most common form is k-Fold Cross-Validation, where the data is split into k equal-sized folds. In each of the k iterations, k-1 folds are used for training, and the remaining fold is used for validation [11].

Bootstrapping is another powerful resampling technique. It involves repeatedly drawing samples from the dataset with replacement to create multiple bootstrap samples of the same size as the original dataset [4] [11]. Each bootstrap sample is used to train a model, and the model is then evaluated on the data points not selected in the sample, known as the Out-of-Bag (OOB) data [4]. This method is particularly valued for its ability to estimate the variability of performance metrics.

The table below summarizes the key characteristics of these two methods, highlighting their fundamental differences.

Table 1: Key Differences Between Cross-Validation and Bootstrapping

Aspect Cross-Validation Bootstrapping
Definition Splits data into k subsets (folds) for training and validation. Samples data with replacement to create multiple bootstrap datasets.
Data Partitioning Mutually exclusive subsets; no overlap between training/test sets in an iteration. Samples contain repeated instances; some data points are omitted (OOB data).
Bias & Variance Generally offers a lower variance estimate, but may have higher bias with a low k. Can provide a lower bias estimate but may have higher variance due to resampling.
Primary Purpose Estimate model performance and generalize to unseen data; model selection. Estimate the variability of a statistic or model performance; assess uncertainty.
Ideal Use Case Model comparison, hyperparameter tuning with balanced, large-enough datasets. Small datasets, variance estimation, or when the dataset has significant noise.

Best Practices for Data Preprocessing in Validation Loops

The Paramount Rule: Preventing Data Leakage

The most critical principle when preprocessing data for validation loops is preventing data leakage. Data leakage occurs when information from the validation set inadvertently influences the training process [71]. This leads to overly optimistic performance estimates and models that fail to generalize. A common source of leakage is performing preprocessing steps, such as scaling or imputation, on the entire dataset before splitting it into training and validation sets. This allows the training process to "peek" at the global statistics (e.g., mean, standard deviation) of the validation set.

Best Practice: All preprocessing steps must be learned from the training data alone and then applied to the validation set. For example, the mean and standard deviation for scaling should be calculated exclusively from the training fold. This fit must then be used to transform both the training and the validation folds [70]. The use of machine learning pipelines is highly recommended to encapsulate preprocessing and modeling into a single object, ensuring this rule is automatically followed during cross-validation [70].

Essential Data Preprocessing Steps

Data preprocessing is a foundational step, with data practitioners spending around 80% of their time on these tasks [72] [73]. The following steps are crucial within a validation framework:

  • Handling Missing Values: Datasets often have missing values that must be addressed. Strategies include removing rows with missing values or imputing them using statistics like the mean, median, or mode. Critically, any imputation must be based only on the training data [72].
  • Encoding Categorical Data: Machine learning algorithms require numerical input. Non-numerical data (e.g., drug compound structures, lab locations) must be converted into numerical form using techniques like one-hot encoding. Again, the encoding mapping must be derived from the training set [72].
  • Feature Scaling: Many algorithms perform better when features are on a similar scale. Common techniques include Standard Scaler (centering around zero with a standard deviation of one) and Robust Scaler (using median and interquartile range, ideal for data with outliers). The scaling parameters (e.g., mean, standard deviation) must be fit on the training data [72].

Table 2: Common Data Preprocessing Techniques and Applications

Technique Description Best Used When
Mean/Median Imputation Replaces missing values with the feature's mean or median. Data is missing at random; a quick, simple solution is needed.
Standard Scaler Standardizes features by removing the mean and scaling to unit variance. Features are approximately normally distributed.
Robust Scaler Scales features using statistics that are robust to outliers (median & IQR). The dataset contains significant outliers.
One-Hot Encoding Creates binary columns for each category of a categorical variable. Dealing with nominal categories without an inherent order.

The following workflow diagram illustrates the correct integration of data preprocessing within a k-fold cross-validation loop, ensuring no data leakage occurs.

preprocessing_workflow Start Full Dataset Split Split into K Folds Start->Split LoopStart For i = 1 to K Split->LoopStart DefineTrain Define Training Set: K-1 Folds LoopStart->DefineTrain DefineTest Define Validation Set: 1 Fold DefineTrain->DefineTest PreprocessTrain Fit Preprocessor (e.g., Scaler, Imputer) on Training Set DefineTest->PreprocessTrain ApplyTrain Transform Training Set PreprocessTrain->ApplyTrain ApplyTest Transform Validation Set using fitted Preprocessor PreprocessTrain->ApplyTest Prevent Leakage TrainModel Train Model on Processed Training Set ApplyTrain->TrainModel Evaluate Evaluate Model on Processed Validation Set ApplyTest->Evaluate TrainModel->Evaluate EndLoop Next i Evaluate->EndLoop EndLoop->LoopStart Loop Final Average Performance Across All Folds EndLoop->Final

Best Practices for Hyperparameter Tuning in Validation Loops

Tuning Methodologies

Hyperparameters are configuration variables that govern the training process itself, such as the learning rate or the depth of a tree. Tuning them is essential for optimizing model performance [74] [75]. The two most common strategies for tuning within validation loops are:

  • GridSearchCV: A brute-force method that exhaustively tries every combination of hyperparameters from a pre-defined grid. It is guaranteed to find the best combination within the grid but becomes computationally intractable as the number of hyperparameters grows [74].
  • RandomizedSearchCV: This method randomly samples a fixed number of hyperparameter combinations from a specified distribution. It is often more efficient than grid search, as it can find a good combination with fewer iterations, especially when some hyperparameters have a minimal impact on performance [74].
The Necessity of Nested Validation

A major pitfall in model development is using the same validation set to both tune hyperparameters and estimate the model's final performance. This practice optimistically biases the performance estimate because the model has been indirectly fitted to the validation set during tuning [71].

Best Practice: To obtain an unbiased performance estimate, a nested cross-validation (or nested bootstrap) protocol should be employed. This involves two layers of validation loops:

  • Inner Loop: Used for hyperparameter tuning (e.g., using GridSearchCV with k-folds on the training data).
  • Outer Loop: Used for performance evaluation of the model with the best hyperparameters found in the inner loop.

This complex but crucial workflow is illustrated in the following diagram.

nested_cv Start Full Dataset OuterSplit Split into K Outer Folds Start->OuterSplit OuterLoopStart For i = 1 to K OuterSplit->OuterLoopStart OuterTrain Outer Training Set: K-1 Folds OuterLoopStart->OuterTrain OuterTest Outer Test Set: 1 Fold OuterLoopStart->OuterTest InnerSplit Split Outer Training Set into M Inner Folds OuterTrain->InnerSplit FinalTest Evaluate Final Model on Outer Test Set OuterTest->FinalTest Tune Hyperparameter Tuning (Grid/Random Search) on Inner Folds InnerSplit->Tune BestHP Select Best Hyperparameters Tune->BestHP FinalTrain Train Final Model on entire Outer Training Set using Best Hyperparameters BestHP->FinalTrain FinalTrain->FinalTest OuterLoopEnd Next i FinalTest->OuterLoopEnd OuterLoopEnd->OuterLoopStart Loop FinalScore Final Performance Score (Unbiased Estimate) OuterLoopEnd->FinalScore

Comparative Experimental Data and Protocols

Experimental Protocol for Model Comparison

To objectively compare the performance of models validated using different strategies, the following protocol can be employed:

  • Dataset: Use a benchmark dataset relevant to the domain (e.g., biomedical data from a clinical trial like the PEACE trial [31]).
  • Model Training:
    • For bootstrap validation, produce B=1000 (or more) bootstrap resamples of the training dataset. Train the model on each resample and evaluate it on the corresponding Out-of-Bag (OOB) sample [4].
    • For cross-validation, perform a repeated 5 or 10-fold cross-validation, where the data is split into k folds, and the process is repeated multiple times with different random splits to reduce variance [4] [70].
  • Performance Measurement: For each validation method, compute the performance metric of interest (e.g., accuracy, C-index) for every iteration.
  • Comparison: To compare two different models, compute the paired performance differences (Model A - Model B) for each bootstrap sample or CV fold. Analyze the distribution of these differences (e.g., via a histogram or confidence interval) to determine if one model outperforms the other with statistical significance [4].

Simulation studies have compared these methods for assessing generalization performance. The table below summarizes findings from such research, indicating that there is no single winner, but rather context-dependent recommendations [4].

Table 3: Comparison of Validation Method Performance from Literature

Validation Method Reported Bias Reported Variance Computational Cost Recommended Context
k-Fold Cross-Validation Lower bias with larger k (e.g., 10) [4]. Lower variance due to averaging over multiple folds [11]. Moderate to High (scales with k). General-purpose use; model selection and hyperparameter tuning [11].
Repeated k-Fold CV Very low bias. Very low variance due to multiple random splits [4]. High When seeking the most reliable and stable performance estimates [4].
Bootstrap (.632+) Can be biased in small samples with high signal-to-noise; generally good bias correction [4]. Can have higher variance than CV [11]. High (requires many resamples). Small sample sizes; useful for bias correction [4].
Optimism Bootstrap Performs well under large sample settings [4]. Provides good variance estimates [11]. High When a variance estimate is needed; can be faster than repeated CV [4].

The Scientist's Toolkit: Essential Research Reagents

In computational research, "research reagents" equate to the software tools, libraries, and metrics that are essential for conducting robust experiments. The following table details key solutions for implementing the practices described in this guide.

Table 4: Key Research Reagent Solutions for Computational Experiments

Item / Solution Function / Purpose Example Use Case
Scikit-learn Library A comprehensive open-source library for machine learning in Python. Provides implementations for GridSearchCV, RandomizedSearchCV, KFold, and various preprocessing modules like StandardScaler and SimpleImputer [72] [74].
SHAP (SHapley Additive exPlanations) A game theory-based method to explain the output of any machine learning model. Used in conjunction with AutoML tools or custom models to interpret "black-box" predictions and ensure model decisions are based on chemically or biologically plausible features [76].
Pipeline Abstraction A software construct that chains together preprocessing steps and a model into a single object. Critical for preventing data leakage during cross-validation by ensuring preprocessing is fitted only on the training folds [70].
C-index (Concordance Index) A metric used to evaluate the discriminatory power of a model, especially for survival analysis. The primary performance metric in clinical trial model evaluation, such as in the PEACE trial example for assessing a precision medicine strategy [31].
Bayesian Optimization A sequential design strategy for global optimization of black-box functions that is more efficient than grid or random search. Ideal for tuning hyperparameters of complex, slow-to-train models like deep neural networks, as it reduces the number of model trainings needed [75].

The choice between cross-validation and bootstrapping is not about finding a universally superior method, but rather about selecting the right tool for the specific research context. Cross-validation, particularly repeated 5 or 10-fold, is often preferred for model comparison and hyperparameter tuning due to its good balance between bias and variance [4] [70]. In contrast, bootstrapping is invaluable for small datasets and when an estimate of the performance metric's variability is required [4] [11].

Regardless of the chosen method, the integrity of the validation process hinges on two foundational practices: rigorously preventing data leakage by containing all preprocessing within the training loop, and using nested validation to obtain an unbiased estimate of model performance after hyperparameter tuning. For researchers in drug development and other scientific fields, where model predictions can inform critical decisions, adhering to these best practices is not merely an academic exercise—it is a fundamental requirement for building models that are truly reliable, generalizable, and trustworthy.

Bootstrap validation is a powerful resampling technique used to assess the stability and accuracy of statistical models, particularly in fields like drug development where dataset sizes may be limited. This method operates by creating multiple new datasets from the original data through random sampling with replacement, meaning that some data points may appear multiple times in a given sample while others may be omitted entirely [77]. The central premise of bootstrapping is that the original sample of size n is treated as an empirical representation of the underlying population, and by repeatedly drawing samples of size n from this empirical distribution, we can estimate the variability of model performance and correct for optimism [33].

Within the broader thesis research comparing cross-validation versus bootstrap validation, it is crucial to understand that these methods, while sharing the common goal of providing reliable performance estimates for predictive models, differ fundamentally in their approach to data partitioning [11]. Cross-validation systematically divides data into mutually exclusive folds for training and testing, while bootstrapping employs random sampling with replacement to create datasets that inherently contain duplicates. This fundamental difference in methodology leads to distinct trade-offs between bias and variance in performance estimation, with bootstrap generally providing lower bias but potentially higher variance, especially when dealing with small datasets [11] [44].

The issue of duplicate data points in bootstrapping represents a critical area of investigation because these duplicates directly influence model training and validation metrics. When a model is trained on bootstrap samples containing duplicates, it may appear to perform exceptionally well on those specific repeated observations, potentially leading to overoptimistic performance assessments if not properly corrected [33]. This phenomenon is particularly relevant for pharmaceutical researchers and scientists who rely on accurate model validation to make consequential decisions about drug efficacy and safety.

The Mechanism of Duplicate Formation in Bootstrap

The Bootstrap Sampling Process

The bootstrap algorithm creates new samples through a specific mechanical process that necessarily generates duplicate observations. Beginning with an original dataset containing n observations, the method randomly selects n data points with replacement to form each bootstrap sample [77]. This "with replacement" aspect is fundamental to the bootstrap approach and means that after each selection, the chosen data point is returned to the pool and may be selected again in the same sample. Consequently, each bootstrap sample contains the same number of observations as the original dataset but with a different composition—some observations appear multiple times while others do not appear at all [78].

The mathematical foundation of this process reveals why duplicates are inevitable. When drawing n observations with replacement from a dataset of size n, the probability that any specific observation is excluded from a bootstrap sample is approximately (1-1/n)^n, which approaches 1/e ≈ 0.368 as n becomes large [78]. This means that approximately 36.8% of the original observations are typically excluded from any given bootstrap sample, while the remaining 63.2% form the sample, with many appearing multiple times to maintain the sample size of n.

Illustrative Example of Bootstrap Sampling

Consider a simple dataset with five observations: [2, 4, 6, 8, 10]. When applying bootstrapping, we might generate a new sample such as [4, 4, 6, 10, 2], where the value '4' appears twice, the values '2', '6', and '10' appear once, and the value '8' does not appear at all [77]. This example demonstrates concretely how the bootstrap mechanism naturally produces datasets with duplicate entries while simultaneously excluding some original observations.

The diagram below visualizes this bootstrap sampling process and the inherent creation of duplicate data points:

bootstrap_process OriginalDataset Original Dataset (5 observations: 2, 4, 6, 8, 10) Sampling Random Sampling with Replacement OriginalDataset->Sampling BootstrapSample Bootstrap Sample (5 observations: 4, 4, 6, 10, 2) Sampling->BootstrapSample Duplicates Duplicate: '4' appears twice BootstrapSample->Duplicates Omitted Omitted: '8' not included BootstrapSample->Omitted

The Overfitting Mechanism of Duplicate Data

How Duplicates Inflate Apparent Performance

Duplicate data points in bootstrap samples create conditions conducive to overfitting through several interconnected mechanisms. When a model encounters the same observation multiple times during training, it can disproportionately learn the specific patterns—both signal and noise—associated with those repeated observations [79]. This specialized learning leads to artificially enhanced performance metrics when the model is evaluated on the bootstrap sample itself, as it has effectively "memorized" a portion of the training data rather than learning generalizable patterns [80].

The overfitting phenomenon occurs because machine learning models, when trained on datasets containing duplicates, begin to fit not only the underlying true relationship between variables (the signal) but also the random fluctuations specific to those duplicated observations (the noise) [80]. In technical terms, the model's variance increases as it becomes more sensitive to the particular composition of the bootstrap sample rather than the general population distribution. This is particularly problematic for complex models with high capacity, such as deep neural networks or decision trees, which can easily memorize specific data points when they appear repeatedly in training [80].

The Optimism Bootstrap Correction

Recognizing this inherent bias, statisticians have developed correction methods, most notably the optimism bootstrap approach [33]. This technique quantitatively estimates the overfitting caused by duplicates and adjusts performance metrics accordingly. The correction process follows a specific protocol:

  • Calculate the model's performance on the bootstrap sample (which contains duplicates)
  • Calculate the model's performance on the original dataset
  • Compute the difference between these two metrics (the "optimism")
  • Subtract this optimism from the apparent performance of the final model

The mathematical implementation can be represented as:

optimism_correction TrainPerformance Performance on Bootstrap Sample (With Duplicates) Optimism Calculate Optimism (Train Performance - Test Performance) TrainPerformance->Optimism TestPerformance Performance on Original Data TestPerformance->Optimism CorrectedPerformance Bias-Corrected Performance (Original Performance - Average Optimism) Optimism->CorrectedPerformance

This approach acknowledges and quantitatively addresses the overfitting induced by duplicate points, providing a more realistic estimate of how the model will perform on truly independent data [33].

Comparative Analysis: Bootstrap versus Cross-Validation

Fundamental Methodological Differences

When evaluating model performance, researchers must understand the distinct approaches of bootstrap and cross-validation techniques. The following table summarizes their key characteristics:

Aspect Bootstrap Validation Cross-Validation
Data Partitioning Samples with replacement to create datasets of same size as original Splits data into k mutually exclusive folds
Sample Composition Contains duplicates (~63.2% of original data with repetitions) Unique subsets with no overlap between training and test sets
Bias-Variance Trade-off Lower bias (uses full dataset) but potentially higher variance Generally lower variance but may have higher bias with small k
Computational Intensity Moderate (typically 200-500 samples) High for large k or repeated iterations
Best Application Context Small datasets, uncertainty estimation Model comparison, hyperparameter tuning
Duplicate Data Handling Inherently generates duplicates requiring correction No duplicates in training-test splits

This comparative analysis reveals that bootstrap's inclusion of duplicate data points is both its strength and weakness—it allows for more efficient use of limited data but introduces potential overfitting that must be explicitly corrected [11] [44].

Visual Comparison of Methodologies

The fundamental structural differences between these validation approaches can be visualized as follows:

validation_comparison cluster_bootstrap Bootstrap Approach cluster_cv Cross-Validation Approach OriginalData Original Dataset BSample1 Bootstrap Sample 1 (With Duplicates) OriginalData->BSample1 BSample2 Bootstrap Sample 2 (With Duplicates) OriginalData->BSample2 BSampleN ... Bootstrap Sample B OriginalData->BSampleN Fold1 Fold 1: Test Set OriginalData->Fold1 Fold2 Fold 2: Test Set OriginalData->Fold2 FoldK Fold K: Test Set OriginalData->FoldK BTraining Training: 100% of BSample (Contains ~63.2% unique data) BSample1->BTraining BTesting Testing: Original Data BSample1->BTesting CVTraining1 Training: Folds 2-K (90% of data for k=10) Fold1->CVTraining1 CVTraining2 Training: Folds 1,3-K (90% of data for k=10) Fold2->CVTraining2 CVTrainingK Training: Folds 1-(K-1) (90% of data for k=10) FoldK->CVTrainingK

Experimental Protocols for Evaluating Duplicate-Induced Overfitting

Standard Bootstrap Validation Protocol

Researchers can implement the following experimental protocol to quantitatively assess the impact of duplicate data points on model overfitting:

  • Dataset Preparation: Begin with a complete dataset of n observations with known outcomes. For drug development contexts, this might include molecular descriptors, assay results, or clinical trial data.

  • Bootstrap Sample Generation: Create B bootstrap samples (typically B=200-500) by sampling n observations with replacement from the original dataset. Record the frequency of each observation across all bootstrap samples.

  • Model Training: Train identical model architectures on each bootstrap sample. For pharmaceutical applications, this might include logistic regression models for compound classification or Cox proportional hazards models for survival analysis.

  • Performance Assessment: Calculate performance metrics (e.g., Somers' D, c-index, Brier score) for each model on both:

    • The bootstrap sample used for training (containing duplicates)
    • The original full dataset

  • Optimism Calculation: For each bootstrap iteration, compute the optimism as the difference between the performance on the bootstrap sample and the performance on the original dataset [33].

  • Bias Correction: Calculate the average optimism across all B bootstrap samples and subtract this from the apparent performance of the final model (trained on the complete original dataset).

This protocol directly quantifies how duplicate observations inflate performance metrics and provides a mechanism for correction.

Comparative Cross-Validation Protocol

To contextualize bootstrap results, implement parallel k-fold cross-validation:

  • Data Partitioning: Randomly divide the dataset into k folds (typically k=5 or k=10), ensuring representative distribution of outcomes in each fold.

  • Iterative Training: For each fold i:

    • Train the model on the combined k-1 folds
    • Validate on the held-out fold i
    • Record performance metrics

  • Performance Aggregation: Calculate mean performance across all k folds along with variability measures.

This approach provides a reference point for evaluating whether bootstrap-corrected performance metrics align with cross-validation estimates.

Key Research Reagents and Computational Tools

Implementation of these experimental protocols requires specific computational tools and statistical packages:

Research Tool Function Implementation Example
R Statistical Environment Primary platform for bootstrap implementation Comprehensive bootstrap and CV functions
boot Package (R) Bootstrap sampling and validation boot() function for custom bootstrap procedures
rms Package (R) Regression modeling and validation validate() function for optimism bootstrap correction
Hmisc Package (R) Statistical analysis and performance metrics somers2() function for Somers' D calculation
Python scikit-learn Alternative implementation platform BaggingClassifier for ensemble methods
mlfinlab Package Specialized bootstrap for financial data Sequential bootstrapping for dependent data

These tools enable researchers to implement the described protocols and quantitatively evaluate the impact of duplicate-induced overfitting in their specific applications [33] [81].

Empirical Data on Duplicate-Induced Overfitting

Quantitative Evidence from Case Studies

Empirical studies provide concrete evidence of how duplicate data points in bootstrap samples lead to overoptimistic performance assessments. In a case study evaluating logistic regression models for predicting low infant birth weight, researchers observed measurable differences between apparent and corrected performance metrics [33]. The study implemented the optimism bootstrap approach with 200 bootstrap samples and reported the following results:

Performance Metric Apparent Performance Bias-Corrected Performance Optimism
Somers' D 0.438 0.425 0.013
C-index (AUC) 0.719 0.712 0.007

This quantitative evidence demonstrates that bootstrap samples containing duplicates systematically inflate performance metrics, with the optimism correction reducing Somers' D by approximately 3% in this specific application [33].

Comparative Performance Across Methods

Research comparing bootstrap and cross-validation approaches has revealed consistent patterns in their performance estimation characteristics. A comprehensive analysis discussed on statistical forums indicated that repeated 10-fold cross-validation (100 repetitions) and the Efron-Gong optimism bootstrap generally provide comparable performance estimates for non-extreme cases where the number of observations exceeds the number of features (n > p) [44]. However, in extreme scenarios with more features than observations (p > n), cross-validation demonstrates superior performance as bootstrap methods may become unstable [44].

The table below summarizes typical performance differences observed in empirical comparisons:

Validation Method Relative Bias Relative Variance Optimal Use Case
Optimism Bootstrap Low Moderate Small to medium datasets (n < 1000)
0.632 Bootstrap Very Low Moderate Discontinuous accuracy measures
10-fold CV Moderate Low Balanced datasets, model comparison
Repeated 10-fold CV Low Very Low Extreme cases (p > n)

These empirical findings underscore the importance of selecting validation methods appropriate to specific dataset characteristics and research contexts [44].

Mitigation Strategies for Duplicate-Induced Overfitting

Technical Approaches for Pharmaceutical Applications

Researchers in drug development can employ several specific strategies to address the overfitting risks associated with duplicate data points in bootstrap validation:

  • Implement Optimism Correction: Always apply the optimism bootstrap approach rather than naive bootstrap validation. This method explicitly quantifies and corrects for the overfitting induced by duplicate observations [33].

  • Utilize the 0.632 Bootstrap Rule: For certain performance metrics, particularly those with discontinuous scoring rules, the 0.632 bootstrap method has been shown to outperform standard optimism correction. This approach uses a weighted average of the apparent performance and the performance on out-of-bag samples [44].

  • Apply Sequential Bootstrapping for Dependent Data: In time-series pharmaceutical data (e.g., longitudinal clinical trials), standard bootstrap assumptions of independent observations are violated. Sequential bootstrapping preserves temporal dependencies while minimizing overlap between samples, effectively reducing the problematic aspects of duplication [81].

  • Leverage m-out-of-n Bootstrap: For datasets with complex structures or high dimensionality, sampling m observations where m < n can provide more reliable performance estimates, though this approach requires careful selection of the appropriate m value [26].

  • Implement Rigorous Process Repetition: Ensure that all supervised learning steps, including any feature selection or hyperparameter tuning, are repeated afresh for each bootstrap sample. Failure to do so will result in underestimation of true overfitting [44].

Decision Framework for Method Selection

Pharmaceutical researchers can use the following decision framework to select appropriate validation strategies:

decision_framework Start Start: Validation Method Selection Q1 Dataset Size < 100 observations? Start->Q1 Q2 Number of Features > Number of Observations? Q1->Q2 No BootstrapRec Recommended: Optimism Bootstrap Q1->BootstrapRec Yes Q3 Temporal Dependencies in Data? Q2->Q3 No CVRec Recommended: Repeated 10-fold CV Q2->CVRec Yes Q4 Primary Goal: Model Selection or Performance Estimation? Q3->Q4 No SeqBootstrapRec Recommended: Sequential Bootstrap Q3->SeqBootstrapRec Yes Q4->CVRec Model Selection BothRec Recommended: Both Methods for Verification Q4->BothRec Performance Estimation

The presence of duplicate data points in bootstrap samples represents a fundamental characteristic of the method that directly contributes to overfitting if not properly addressed. Through systematic comparison with cross-validation approaches, we have demonstrated that bootstrap validation offers distinct advantages for small datasets and uncertainty estimation but requires specific correction mechanisms to account for the inflationary effect of duplicates on performance metrics.

For researchers and drug development professionals, the key insight is that duplicate-induced overfitting is not a reason to avoid bootstrap methods but rather a factor that must be explicitly quantified and corrected through established techniques like the optimism bootstrap. When implemented with appropriate corrections and in the right contextual applications (particularly with small to medium-sized datasets), bootstrap validation provides powerful and efficient model assessment that complements rather than competes with cross-validation approaches.

The empirical evidence consistently shows that properly corrected bootstrap methods yield performance estimates comparable to repeated cross-validation while offering computational advantages in many scenarios. By understanding the mechanisms of duplicate-induced overfitting and implementing appropriate mitigation strategies, researchers can confidently employ bootstrap validation as part of a comprehensive model assessment toolkit in pharmaceutical research and development.

Evidence-Based Comparison: Choosing the Right Tool for Your Research

In the development of predictive models for biomedical research, robust internal validation is paramount to ensure that performance estimates accurately reflect a model's generalizability to new data. Cross-validation and bootstrap validation represent two of the most prominent resampling techniques used for this purpose. However, these methods differ substantially in their computational approaches, statistical properties, and susceptibility to bias and variance, creating a critical need for direct comparison of their performance characteristics. This guide synthesizes evidence from simulation studies to objectively compare the precision and bias of these validation methodologies across various clinical prediction scenarios. Framed within a broader thesis on validation comparison research, this analysis provides drug development professionals and researchers with empirical data to inform their validation strategy selection, particularly addressing the tradeoffs inherent in high-dimensional, low-sample-size settings common in biomedical applications.

Comparative Performance of Validation Methods

Quantitative Performance Metrics Across Simulation Studies

Table 1: Performance comparison of internal validation methods across simulation studies

Validation Method Scenario/Condition Performance Metric Result Value Bias Direction Key Findings
K-fold Cross-Validation High-dimensional time-to-event (n=50-100) [6] Discriminative Performance Stable Low optimism Recommended for Cox penalized models with sufficient samples
Bootstrap (.632+) Small samples, regularized estimation [29] C-statistic RMSE Comparable/Larger Slight underestimation (small events) Performs well under small samples except with regularized methods
Conventional Bootstrap High-dimensional prognosis [6] Optimism Correction Over-optimistic Overestimation Over-optimistic bias in high-dimensional settings
Bootstrap (.632) Small samples, larger event fraction [29] C-statistic Biased Overestimation Overestimation bias when event fraction becomes larger
Harrell's Bootstrap Small samples, larger event fraction [29] C-statistic Biased Overestimation Similar overestimation as .632 method
Train-Test Split High-dimensional settings [6] Performance Stability Unstable Variable Unstable performance across simulations
Nested Cross-Validation High-dimensional time-to-event [6] Discriminative Performance Fluctuating Variable Performance fluctuates with regularization method
Cross-Validation vs. Holdout PET data for DLBCL patients [82] AUC SD 0.06 vs 0.07 Comparable Comparable performance, lower uncertainty with CV

Bias-Variance Tradeoffs Across Sample Sizes and Data Types

Simulation studies consistently reveal that the relative performance of cross-validation versus bootstrap methods is highly dependent on sample size, data dimensionality, and model characteristics. In high-dimensional prognosis settings with time-to-event outcomes, k-fold cross-validation demonstrates greater stability compared to bootstrap approaches, with conventional bootstrap methods showing over-optimistic bias while the .632+ variant tends toward excessive pessimism, particularly with small sample sizes (n=50 to n=100) [6]. For multivariable prediction models using logistic regression, all three bootstrap-based optimism correction methods (Harrell's, .632, and .632+) perform comparably well under large-sample conditions where events per variable (EPV) ≥10. However, under small-sample settings, both Harrell's and the .632 method exhibit overestimation biases with larger event fractions, while the .632+ method shows slight underestimation bias with very small event fractions [29].

A direct comparison of cross-validation versus holdout validation in simulated positron emission tomography (PET) data for diffuse large B-cell lymphoma patients revealed that fivefold repeated cross-validation (CV-AUC: 0.71±0.06) and holdout validation (AUC: 0.70±0.07) produced comparable discrimination performance, though the holdout approach exhibited higher uncertainty [82]. Bootstrapping in the same simulation yielded a lower CV-AUC of 0.67±0.02, suggesting potentially greater pessimism in this clinical prediction context. These findings underscore the context-dependent nature of validation performance and the importance of selecting methods aligned with specific research constraints.

Experimental Protocols and Methodologies

Simulation Design for High-Dimensional Time-to-Event Data

Protocol 1: Internal validation strategy for high-dimensional prognosis models [6]

  • Data Generation: Simulated datasets were generated using data from the SCANDARE head and neck cohort (N=76 patients) incorporating clinical variables (age, sex, HPV status, TNM staging) and transcriptomic data (15,000 transcripts) with disease-free survival outcomes and realistic cumulative baseline hazard.

  • Sample Sizes: Multiple sample sizes were simulated (N=50, 75, 100, 500, 1000) with 100 replicates for each condition to assess stability across different data scenarios.

  • Model Development: Cox penalized regression was performed for model selection with regularization to handle high-dimensional predictors.

  • Validation Methods: Each simulation applied multiple internal validation strategies: train-test (70% training), bootstrap (100 iterations), 5-fold cross-validation, and nested cross-validation (5×5 configuration).

  • Performance Metrics: Evaluated discriminative performance using time-dependent AUC and C-index, and calibration using 3-year integrated Brier Score to comprehensively assess model performance.

  • Comparison Analysis: Method performance was compared across sample sizes and replication runs to identify optimal validation approaches for high-dimensional time-to-event data.

Simulation Protocol for Multivariable Prediction Models

Protocol 2: Comparing bootstrap-based optimism correction methods [29]

  • Data Foundation: Simulation data were generated based on the Global Utilization of Streptokinase and Tissue plasminogen activator for Occluded coronary arteries (GUSTO-I) trial Western dataset to ensure clinical relevance.

  • Experimental Conditions: Simulations systematically varied key parameters: events per variable (EPV), event fraction, number of candidate predictors, and magnitude of regression coefficients for predictors.

  • Modeling Strategies: Multiple model building approaches were implemented: conventional logistic regression, stepwise variable selection, Firth's penalized likelihood method, ridge regression, lasso regression, and elastic-net regression.

  • Bootstrap Methods: Three bootstrap-based correction methods were compared: Harrell's bias correction, the .632 estimator, and the .632+ estimator, with focus on internal validity of C-statistics.

  • Evaluation Metrics: Performance was assessed through bias analysis and root mean squared error (RMSE) calculations across 100 simulation replicates for each condition to ensure statistical reliability.

  • Software Implementation: All analyses were performed using R version 3.5.1 with specialized packages (logistf for Firth's method, glmnet for regularized regression, rms for Harrell's method) to ensure methodological consistency.

Workflow Visualization of Validation Methods

K-Fold Cross-Validation Methodology

kfold_cv cluster_loop Repeat for K Iterations start Start with Full Dataset split Split Data into K Folds start->split fold_i Use Fold i as Test Set Remaining K-1 Folds as Training split->fold_i train Train Model on Training Set fold_i->train test Evaluate Model on Test Set train->test store Store Performance Metric test->store combine Combine K Performance Metrics for Final Estimate store->combine

Bootstrap Resampling Methodology

bootstrap cluster_loop Repeat for B Bootstrap Samples start Start with Original Dataset (n) resample Draw Bootstrap Sample (n observations with replacement) start->resample train Train Model on Bootstrap Sample resample->train test_orig Test Model on Original Dataset train->test_orig test_boot Test Model on Bootstrap Sample train->test_boot calculate Calculate Optimism test_orig->calculate test_boot->calculate correct Apply Optimism Correction to Apparent Performance calculate->correct

The Scientist's Toolkit: Research Reagent Solutions

Table 2: Essential computational tools for validation method implementation

Tool/Resource Function/Purpose Implementation Example
R Statistical Software Primary platform for implementing validation methods Version 3.5.1 or higher for compatibility with validation packages [29]
glmnet Package Regularized regression implementation Used for ridge, lasso, and elastic-net regression with 10-fold CV for tuning parameters [29]
rms Package Harrell's bootstrap validation Implements Harrell's bias correction method for multivariable prediction models [29]
logistf Package Firth's penalized likelihood method Addresses small-sample bias and complete separation in logistic regression [29]
Custom Simulation Frameworks Generating synthetic data with known properties Creates calibrated datasets for method comparison while protecting patient privacy [83]
Nested Cross-Validation Hyperparameter tuning and performance estimation 5×5 configuration for optimal bias-variance tradeoff in high-dimensional settings [6]
Repeated Cross-Validation Stability assessment of performance estimates 100 repeats of 5-fold CV for precise performance estimation [82]

This direct performance comparison reveals that neither cross-validation nor bootstrap validation universally dominates across all scenarios in biomedical research. The optimal choice depends critically on specific research constraints: k-fold cross-validation demonstrates superior stability for high-dimensional time-to-event data with sufficient sample sizes, while bootstrap methods (.632+ variant) show advantages in small-sample settings except when using regularized estimation methods. For drug development professionals working with molecular data or complex clinical prediction models, these findings underscore the importance of aligning validation strategies with specific data characteristics, particularly dimensionality, sample size, and event rates. The experimental protocols and workflow visualizations provided herein offer practical guidance for implementing these validation approaches, while the reagent toolkit equips researchers with essential computational resources. As predictive modeling continues to evolve in biomedical research, this empirical comparison framework provides a foundation for selecting validation methods that optimally balance precision and bias for specific research contexts.

In the development of robust predictive models, particularly within scientific and clinical domains, accurately estimating a model's performance on unseen data is paramount. This process of internal validation ensures that models are truly generalizable and not merely overfitting to the noise in a specific sample. Among the various resampling techniques, cross-validation and bootstrapping are two foundational methods [11]. While both aim to provide a reliable measure of model performance, they possess distinct characteristics that make them suitable for different tasks. This guide focuses on the specific scenarios where cross-validation is the preferred choice, particularly for the critical tasks of model comparison and hyperparameter tuning, framing this discussion within broader research comparing it to bootstrapping.

Core Concepts and Definitions

What is Cross-Validation?

Cross-validation is a model validation technique that assesses how the results of a statistical analysis will generalize to an independent dataset [84]. Its primary goal is to simulate the model's performance on unseen data, thus flagging problems like overfitting [21]. The most common implementation is k-fold cross-validation, which works as follows [11] [21]:

  • The dataset is randomly partitioned into k equal-sized subsets (folds).
  • A model is trained using k-1 of the folds as training data.
  • The resulting model is validated on the remaining hold-out fold.
  • This process is repeated k times, with each fold used exactly once as the validation set.
  • The k performance results are averaged to produce a single, more robust estimate.

Table 1: Common Types of Cross-Validation

Type Description Best Use Cases
k-Fold Divides data into k folds; each fold serves as a validation set once [11]. General purpose model evaluation [85].
Stratified k-Fold Preserves the percentage of samples for each class in every fold [11]. Classification with imbalanced datasets [11] [3].
Leave-One-Out (LOOCV) A special case where k equals the number of data points; one sample is left out for validation each time [11]. Very small datasets [11].
Nested CV Uses an outer loop for model assessment and an inner loop for hyperparameter tuning [3]. Providing an unbiased performance estimate when also tuning hyperparameters [3].

What is Bootstrapping?

Bootstrapping is a resampling technique that involves repeatedly drawing samples from the dataset with replacement [11]. In model validation, multiple bootstrap samples (e.g., B=1000) are created. For each sample, a model is trained and then evaluated on the data points not included in the sample, known as the out-of-bag (OOB) data [11] [4]. The results are then aggregated across all iterations. Its strengths lie in estimating the variability of performance metrics and is particularly useful for small datasets [11] [8].

The following workflow diagrams the core procedures for both k-Fold Cross-Validation and the Bootstrapping method, highlighting their structural differences.

cv_workflow Figure 1. K-Fold Cross-Validation Workflow Start Start: Original Dataset Split Split into k Folds Start->Split Loop For each of k iterations: Split->Loop Train Train model on k-1 folds Loop->Train Validate Validate on the 1 held-out fold Train->Validate Validate->Loop Aggregate Aggregate (Average) k Results Validate->Aggregate after k iterations

bootstrap_workflow Figure 2. Bootstrapping (with OOB) Workflow Start Start: Original Dataset Loop For each of B iterations: Start->Loop Sample Draw bootstrap sample (with replacement) Loop->Sample Train Train model on bootstrap sample Sample->Train Validate Validate on Out-of-Bag (OOB) Data Train->Validate Validate->Loop Aggregate Aggregate (Average) B Results Validate->Aggregate after B iterations

Direct Comparison: Cross-Validation vs. Bootstrapping

The choice between cross-validation and bootstrapping is not about which is universally better, but which is more appropriate for a given context. The table below summarizes their key differences.

Table 2: Cross-Validation vs. Bootstrapping - A Detailed Comparison

Aspect Cross-Validation Bootstrapping
Core Principle Splits data into k mutually exclusive subsets (folds) [11]. Samples data with replacement to create multiple bootstrap datasets [11].
Primary Strength Provides a less biased estimate for model comparison and tuning, especially in low-dimensional settings [85]. Effectively captures uncertainty and variability of a performance metric; good for small datasets [11] [8].
Key Weakness Can have higher variance in performance estimates, especially with small k or small datasets [11] [4]. Can introduce more bias and overestimate performance due to sample similarity [11] [85].
Computational Cost Requires k model fits. Generally efficient for k=5 or 10 [11]. Requires B model fits (often >1000), but can be more precise than a single CV run, potentially requiring fewer total fits than repeated CV [4].
Ideal Dataset Size Medium to large datasets [8]. Small datasets (e.g., n < 200) [8].
Best for Model Comparison Yes. Directly facilitates comparing different algorithms by averaging performance over multiple, structured test sets [86]. Less straightforward, as bootstrap samples overlap.
Best for Hyperparameter Tuning Yes. Widely considered the standard, supported by extensive simulation studies [87] [85]. Can be used, but may show a slight tendency toward worse model calibration compared to CV [85].

When to Prefer Cross-Validation: The Evidence

For Hyperparameter Tuning

Hyperparameter tuning is the process of finding the optimal configuration of a model's parameters that cannot be directly learned from the data. Cross-validation, particularly k-fold CV, is the gold standard for this task.

  • Experimental Evidence: A comprehensive 2024 simulation study by Zoë S. Dunias et al. compared hyperparameter tuning procedures for clinical prediction models. The study found that standard 5-fold and 10-fold cross-validation "performed similarly well and outperformed the other tuning procedures," including bootstrap-based methods. The study further concluded that bootstrap tuning showed a "slight tendency to more severe miscalibration" than CV [85].
  • Why it Works: CV provides a reliable out-of-sample estimate of performance for each hyperparameter candidate. By averaging over k folds, it reduces the risk of selecting hyperparameters that are overfit to a single, arbitrary train-validation split [21]. This is typically implemented in practice using GridSearchCV or RandomizedSearchCV in libraries like Scikit-Learn, which automate the process of tuning hyperparameters via cross-validation [87].

For Model Comparison

When deciding between different modeling algorithms (e.g., Lasso vs. Random Forest), the goal is to identify which one has better inherent generalizability.

  • Theoretical Foundation: Cross-validation is ideally suited for this because it creates multiple, independent test sets. The performance of each model is averaged across these sets, providing a stable and comparable metric [86]. This process directly estimates how each model would perform on unseen data.
  • Practical Application: In a tutorial on health care modeling, cross-validation was highlighted as a key method for comparing models on real-world electronic health record data, helping to ensure that the chosen model will generalize to new patient populations [3].
  • Contrast with Bootstrapping: While bootstrap can be used for model comparison by examining the distribution of performance differences on OOB samples [4], the correlated nature of bootstrap samples can make the procedure less direct and the results potentially less intuitive than the structured folds of CV.
  • Medium to Large Datasets: Where data is sufficient to split into meaningful folds without losing significant statistical power in the training set [8].
  • Balanced Datasets: Or when using Stratified k-Fold to handle class imbalances [11] [3].
  • Computational Efficiency is a Concern: Using k=5 or 10 is often computationally cheaper than running thousands of bootstrap iterations while still providing excellent performance estimates [11] [85].
  • High-Dimensional Data: In settings like genomics (e.g., GWAS), bootstrapping can overfit due to repeated sampling of the same individuals, making CV the safer choice [8].

Experimental Protocols and Data

This section outlines a standard protocol for using cross-validation in a model selection and tuning pipeline, a common scenario in research.

Detailed Methodology: Nested Cross-Validation

Nested cross-validation is the recommended protocol for when you need to both tune a model's hyperparameters and get an unbiased estimate of its performance for comparison with other models [3].

  • Define an Outer Loop (Model Assessment): Split the entire dataset into k outer folds (e.g., k=5 or 10).
  • Define an Inner Loop (Hyperparameter Tuning): For each outer fold: a. The k-1 folds designated as the training set in the outer loop are used for model development. b. A separate k-fold cross-validation (the inner loop) is performed on this outer training set to tune the model's hyperparameters (e.g., via Grid Search). c. The best hyperparameters from the inner loop are used to train a final model on the entire outer training set.
  • Validate Model: This final model is evaluated on the held-out outer test fold.
  • Repeat and Aggregate: The process is repeated for each of the k outer folds. The final performance estimate is the average of the scores on the outer test folds.

Quantitative Data from Simulation Studies

The following table summarizes key findings from the 2024 simulation study cited earlier, which provides empirical support for preferring cross-validation in specific contexts [85].

Table 3: Summary of Tuning Procedure Performance from Dunias et al. (2024)

Tuning Procedure Discrimination (AUC/C-index) Calibration Performance Overall Recommendation
Standard 5/10-Fold CV Similar to other top procedures Well-calibrated, outperformed others Supported - Minimizes out-of-sample error reliably.
Repeated CV Similar to standard CV Similar to standard CV No clear benefit over standard CV despite higher cost.
Bootstrap Tuning Similar to other top procedures Slight tendency toward more severe miscalibration Outperformed by standard CV.
1-SE Rule CV Similar to other top procedures Often resulted in severe miscalibration Not recommended for prediction models in low-dimensional settings.

The Scientist's Toolkit: Essential Research Reagents

When implementing cross-validation experiments in a programming environment, several "reagent" tools are essential. The following table lists key components, with a focus on the widely-used Python Scikit-Learn library.

Table 4: Essential Tools for Cross-Validation Experiments

Tool / Reagent Function Example/Notes
cross_val_score Simplifies the process of running k-fold CV and collecting scores for a given model [21]. Quick model evaluation without hyperparameter tuning.
GridSearchCV & RandomizedSearchCV Automates hyperparameter tuning via cross-validation [87]. Exhaustively (Grid) or randomly (Randomized) searches a parameter space. The core utility for integrating tuning with CV.
cross_validate Extends cross_val_score to evaluate multiple metrics and return fit times [21]. More detailed model assessment.
StratifiedKFold A cross-validator that ensures each fold has the same proportion of class labels as the full dataset [11]. Critical for imbalanced classification tasks.
Pipeline Ensures that all preprocessing (e.g., scaling, feature selection) is fitted only on the training fold and applied to the validation fold, preventing data leakage [21]. Essential for producing valid results.
Nested CV Code Template A code structure that implements an outer and inner loop for unbiased evaluation [3]. Can be built using a loop with GridSearchCV inside a cross_validate call.

Within the ongoing research comparing validation techniques, cross-validation establishes itself as the superior method for two fundamental tasks: hyperparameter tuning and model comparison. Empirical evidence from simulation studies confirms that standard k-fold cross-validation provides reliable, well-calibrated performance estimates, often outperforming bootstrapping in these specific contexts [85]. While bootstrapping remains an invaluable tool for assessing estimate variability and working with very small samples [11] [8], researchers and data scientists should preferentially turn to cross-validation when the primary goal is to select the best algorithm or finely tune its parameters for optimal predictive performance on new data.

In the ongoing research comparing cross-validation and bootstrap validation, a clear understanding of the specific scenarios where one method is superior to the other is crucial for building robust predictive models. This guide provides an objective, data-driven comparison for researchers and scientists, focusing on the performance of bootstrapping relative to cross-validation. The analysis confirms that bootstrapping is the preferred technique in two primary scenarios: when working with small sample sizes where data is scarce, and when the research objective requires a precise estimation of the variance or uncertainty associated with a model's performance metrics [32] [11]. The following sections detail the experimental evidence and methodological protocols that support this conclusion.

Performance Comparison: Bootstrapping vs. Cross-Validation

Direct comparisons of bootstrap and cross-validation error estimators reveal distinct performance patterns across different modeling conditions. The following table synthesizes key findings from a simulation study that evaluated both methods using LASSO and Random Forest models on data generated from a causal graph, providing a quantitative basis for comparison [88].

Test Error Estimator Performance with LASSO Model Performance with Random Forest Model Inherent Bias Tendency
Bootstrap Underestimates the true test error [88] Underestimates the true test error [88] Pessimistic; tends to overestimate error [32]
K-Fold Cross-Validation Underestimates the true test error [88] Performs well; provides accurate estimates [88] Less biased but can have higher variance [32]

This experimental data indicates that while both methods can struggle with certain model types, bootstrapping demonstrates a consistent tendency to underestimate test error, a characteristic that researchers must account for during model evaluation.

Advantages of Bootstrapping: Core Use Cases

Estimation with Limited Data

Bootstrapping is exceptionally valuable for small datasets where splitting data into training and test sets, as done in cross-validation, would leave the model with insufficient information to learn effectively [11]. By repeatedly sampling with replacement from the original dataset, bootstrapping allows for the creation of multiple training sets that are each the same size as the original data. This process makes maximal use of all available data points, providing a more stable foundation for model evaluation when samples are limited [22].

Quantifying Uncertainty and Variability

A key strength of bootstrapping is its ability to directly estimate the sampling distribution of almost any statistic, from simple means to complex model parameters [89] [22]. This makes it indispensable for calculating robust measures of uncertainty.

  • Standard Error Estimation: The standard deviation of a statistic (e.g., a regression coefficient, model accuracy) across thousands of bootstrap samples serves as an empirical estimate of its standard error [89] [90].
  • Confidence Interval Construction: Bootstrapping can generate confidence intervals (e.g., by taking the 2.5th and 97.5th percentiles of the bootstrap distribution) without relying on potentially inaccurate normality assumptions, which is particularly useful for statistics with unknown sampling distributions [22] [90].

Experimental Protocols for Bootstrap Validation

For researchers seeking to implement bootstrap validation, the following workflow outlines the standard non-parametric bootstrap procedure for estimating model performance and its variability.

bootstrap_workflow Start Original Sample (Size N) Step1 1. Draw Bootstrap Sample (Sample N times with replacement) Start->Step1 Step2 2. Train Model on Bootstrap Sample Step1->Step2 Step3 3. Calculate Statistic (e.g., Accuracy, Coefficient) Step2->Step3 Step4 4. Repeat B times (typically B >= 1000) Step3->Step4 Step5 5. Analyze Bootstrap Distribution (Calculate SE, CI, Bias) Step4->Step5

The "Analyze Bootstrap Distribution" step involves:

  • Bootstrap Standard Error: Calculated as the standard deviation of the B bootstrap estimates [89] [90].
  • Bootstrap Percentile Confidence Interval: The range between the α/2 and 1-α/2 percentiles (e.g., 2.5th and 97.5th for a 95% CI) of the bootstrap distribution [22].
  • Bootstrap Bias Estimate: The difference between the mean of the bootstrap estimates and the statistic calculated on the original sample [90].

The Scientist's Toolkit: Essential Research Reagents

The table below details key computational tools and conceptual solutions central to implementing and understanding bootstrap validation methods.

Research Reagent / Tool Primary Function Application in Validation
Non-Parametric Bootstrap Empirically approximates the sampling distribution of a statistic by resampling data with replacement [89] [22]. Foundation for estimating standard errors and confidence intervals without parametric assumptions.
Bootstrap Percentile Confidence Interval A confidence interval derived directly from the percentiles of the bootstrap distribution [22] [90]. Provides a range of plausible values for a population parameter; more accurate than t-intervals for larger samples [90].
Out-of-Bag (OOB) Error Estimate The average error when a model is evaluated on data points not included in the bootstrap sample [11]. Serves as an internal, efficient estimate of the test error without needing a separate holdout set.
.632 Bootstrap Rule A weighted average of the error on the bootstrap sample and the OOB error [32]. Corrects for the optimistic bias inherent in the naive bootstrap estimate.
Bootstrap t-Distribution The distribution of bootstrap t-statistics, used to evaluate the accuracy of standard t-intervals [90]. Reveals when traditional t-based inferences are inaccurate (e.g., with skewed data).

Within the broader thesis of cross-validation versus bootstrap validation, bootstrapping establishes its distinct value in addressing specific methodological challenges. The experimental evidence and protocols outlined demonstrate that its primary advantages are realized in contexts of data scarcity and the need for robust variance estimation. For researchers in drug development and other fields where dataset sizes may be limited due to cost or privacy constraints, or where quantifying the uncertainty of a model's output is critical, bootstrapping offers a powerful and flexible solution. A thorough understanding of its properties, particularly its tendency towards pessimistic bias, allows scientists to make an informed choice between resampling methods, ultimately leading to more reliable and interpretable predictive models.

Comparative Analysis of Computational Efficiency and Stability

In the development of robust predictive models, particularly for high-stakes fields like drug development, accurately evaluating model performance is paramount. Two foundational techniques for this internal validation are cross-validation (CV) and bootstrapping. While both methods aim to provide a reliable measure of a model's generalizability to unseen data, they differ significantly in their computational footprint and the stability of their performance estimates. Framed within a broader thesis comparing cross-validation and bootstrap validation, this guide provides an objective comparison of their efficiency and stability, supported by experimental data and detailed protocols to inform researchers and scientists in their selection process.

Core Concepts and Workflows

What are Cross-Validation and Bootstrapping?
  • Cross-Validation (CV): This technique involves partitioning the available dataset into complementary subsets. The model is trained on a subset (the training set) and validated on the remaining subset (the validation or test set). This process is repeated multiple times, and the results are averaged to produce a single, more robust performance estimate [11] [21]. Its primary goal is to estimate how well a model will perform in practice on an independent dataset [70].
  • Bootstrapping: This is a resampling technique that involves drawing multiple random samples from the original dataset with replacement. Each bootstrap sample is used to train a model, which is then evaluated. A key advantage is the automatic creation of an out-of-bag (OOB) sample—the data points not selected in the bootstrap sample—which serves as a natural validation set [11] [4]. It is particularly valued for assessing the variability and stability of performance metrics [11].
Standardized Experimental Workflows

To ensure reproducible and comparable results, the following standardized workflows are recommended.

k-Fold Cross-Validation Workflow

The following diagram illustrates the standard procedure for implementing k-Fold Cross-Validation, a cornerstone of model evaluation.

Detailed Methodology [11] [21] [70]:

  • Data Preparation: Begin with the complete dataset. Shuffle the data to avoid order biases, unless working with time-series data.
  • Folding: Split the dataset into k equal-sized folds. For classification problems with imbalanced classes, use stratified k-fold to preserve the class distribution in each fold [11] [70].
  • Iterative Training & Validation: For k iterations, use the i-th fold as the validation set and the remaining k-1 folds as the training set. In each iteration:
    • Train the model from scratch on the training set.
    • Evaluate the trained model on the validation set, calculating a performance score (e.g., accuracy, F1-score).
    • Store this score.
  • Performance Aggregation: After all k iterations, compute the final model performance estimate by averaging all k validation scores. The standard deviation of these scores can also be calculated to understand variability.
Bootstrapping Workflow

The following diagram illustrates the standard procedure for the bootstrap validation method, highlighting the creation of out-of-bag (OOB) samples.

Detailed Methodology [11] [4]:

  • Initialization: Define the number of bootstrap samples B (typically 200-500).
  • Resampling and Validation: For each of the B iterations:
    • Draw a random sample of size n (the original dataset size) from the training data with replacement. This is the bootstrap sample. On average, this sample contains about 63.2% of the original data points, with some repeated.
    • The data points not included in this sample (approximately 36.8%) form the Out-of-Bag (OOB) sample [4].
    • Train the model on the bootstrap sample.
    • Evaluate the trained model on the OOB sample and record the performance metric.
  • Results Calculation: The final performance estimate is the mean of all OOB scores. The standard deviation of these scores provides a direct measure of the performance metric's stability and variance [11].

Head-to-Head Comparison

Quantitative Performance Data

The following table summarizes key experimental data and recommendations from simulation studies and expert analyses regarding the computational cost and stability of these methods.

Table 1: Comparative Experimental Data on Efficiency and Stability

Aspect Cross-Validation Bootstrapping Supporting Experimental Data / Expert Recommendation
Computational Load High for large k or repeated CV [11]. Demanding for a large number of bootstrap samples B [11]. For precise estimates, 100 repeats of 10-fold CV (1000 model fits) may be needed. The bootstrap typically requires 300-400 repetitions for similar precision, offering a potential speed advantage [44].
Recommended Repetitions 50-100 repeats of 10-fold CV [4] [44]. 200-500 bootstrap samples; 300-400 for stable estimates [4] [44]. The higher number of repetitions for CV is to reduce variance and achieve precision comparable to the bootstrap [4].
Performance Estimate Stability (Variance) Can have high variance, especially with small datasets or a small number of folds [11] [70]. Repeated CV is used to reduce this [4]. Provides an estimate of the variability of the performance metric (e.g., via the standard deviation of OOB scores) [11]. Generally lower uncertainty/variance than k-fold CV [4]. "Out-of-bag bootstrap error rates tend to have less uncertainty/variance than k-fold cross-validation" [4].
Stability in Extreme Settings Robust and recommended for extreme scenarios like N < p (more predictors than samples) [44]. Can be problematic when P >> N (far more predictors than samples) [44]. "10-fold cross-validation repeated 100 times is an excellent competitor... and works even in extreme cases where N < p unlike the bootstrap" [44].
Analysis of Efficiency and Stability
  • Computational Efficiency: While both methods are computationally intensive, the bootstrap often has an edge in non-extreme cases. Achieving a precise estimate with 10-fold CV can require repeating the process 50-100 times, leading to 500-1000 total model fits. In contrast, the bootstrap often produces stable estimates with only 300-400 model fits, resulting in less computation time [4] [44]. However, a single run of k-fold CV (k=5 or k=10) is less intensive than a single run with a large B.
  • Estimate Stability: Stability refers to the consistency of the performance estimate across different data samples.
    • Bootstrap is explicitly designed for variance estimation. The distribution of the OOB scores directly quantifies the stability of the model's performance, making it superior for understanding metric variability [11] [4].
    • Cross-Validation estimates can exhibit higher variance, particularly with small datasets. While the average of k-fields provides a performance estimate, its stability is less directly measured than with bootstrapping. To counteract this, repeated cross-validation is a standard practice to obtain a more stable and reliable mean estimate [4] [70].

The Scientist's Toolkit

This section details key computational and statistical "reagents" essential for implementing the aforementioned experimental protocols.

Table 2: Essential Research Reagents and Tools for Model Validation

Tool / Concept Function / Purpose Relevance in Protocols
Scikit-learn (sklearn) A comprehensive Python library for machine learning. Provides high-level functions like cross_val_score, KFold, and StratifiedKFold to implement cross-validation workflows with minimal code [21].
Stratified K-Fold A variant of k-fold that preserves the percentage of samples for each class in every fold. Critical "reagent" for classification tasks with imbalanced datasets. Ensures that each fold is a representative microcosm of the class structure of the whole dataset, leading to more reliable validation [11] [70].
Pipeline (e.g., sklearn.pipeline) A tool to encapsulate all preprocessing steps (scaling, imputation) and the model into a single object. Prevents data leakage by ensuring that preprocessing steps are fitted only on the training fold within each CV iteration, not on the entire dataset. This is crucial for a rigorous and unbiased evaluation [21] [70].
Out-of-Bag (OOB) Sample The subset of data not included in a bootstrap sample. Serves as a natural, internal validation set for each bootstrap iteration. Eliminates the need for a separate holdout set and is fundamental to the bootstrap validation workflow [11] [4].
Efron-Gong Optimism Bootstrap A specific bootstrap method that estimates the optimism (overfitting) of a model and corrects the apparent performance. A key "reagent" for bias correction. It calculates the difference between performance on the bootstrap sample and the original data, providing a robust estimate of overfitting [4] [44].
Stable Random Seed A fixed number used to initialize a pseudorandom number generator. Ensures the reproducibility of data splitting (folds) and resampling (bootstrap). This is a fundamental practice for obtaining consistent and comparable results across different runs [70].

The choice between cross-validation and bootstrapping involves a direct trade-off between computational efficiency and the depth of stability information.

For researchers and drug development professionals, the following evidence-based guidelines are recommended:

  • Use Bootstrapping when working with small to moderately sized datasets and when quantifying the variance and stability of your performance metric is a priority. Its computational efficiency (300-400 reps) and inherent ability to measure uncertainty make it a powerful choice, provided the number of predictors is not vastly larger than the number of samples [11] [44].
  • Use Cross-Validation when dealing with very large datasets where computational cost is a major concern (a single k-fold run may suffice), when working in high-dimensional settings (N < p), or when a straightforward, easily interpretable validation method is desired. For maximum reliability, repeated (50-100x) 10-fold CV should be employed [4] [44] [8].

In practice, both methods are valid and have similar goals. The decision should be guided by the specific data context, the need for variance estimation, computational constraints, and the overarching requirement for rigorous internal validation in scientific discovery.

This guide provides an objective comparison of two fundamental validation methods in biomedical research: Cross-Validation (CV) and Bootstrap Validation. With the increasing reliance on predictive models for tasks ranging from disease diagnosis to personalized treatment strategies, selecting an appropriate validation framework is crucial for assessing model performance accurately and ensuring reproducible findings. Based on current research, we present a synthesized decision framework to help researchers and drug development professionals choose the optimal validation approach for their specific biomedical application, supported by experimental data and detailed protocols.

In the era of data-driven healthcare, machine learning (ML) and statistical models are prominent tools in biomedical research, encompassing diverse applications such as disease diagnosis, patient risk stratification, and personalized treatment recommendations [31] [19]. The performance of these prediction models must be rigorously evaluated before they can be trusted for clinical or research decision-making. Cross-validation is a widely used technique for evaluating the performance of prediction models, ranging from simple binary classification to complex precision medicine strategies [31]. It helps correct for the optimism bias inherent in evaluating a model on the same data used to train it. More recently, advanced bootstrap methods have been proposed to address some of the computational and statistical challenges associated with cross-validation [31]. This guide directly compares these two methodologies within a structured decision framework tailored for biomedical scenarios, providing the experimental data and protocols necessary for informed method selection.

Methodological Foundations

Cross-Validation (CV)

Core Principle: CV involves splitting the observed dataset into a training set and a testing set, with only the latter being used to evaluate the performance of the model trained on the former. The most common form is K-fold CV, where the data are partitioned into K folds. The model is trained on K-1 folds and tested on the remaining fold; this process is repeated K times until each fold has served as the test set once. The final performance estimate is the average across all K tests [31] [19].

Key Challenge: The resulting CV estimate is a random value dependent on the observed data. Accurately quantifying the uncertainty associated with this estimate is essential, especially when comparing the performance of two models [31]. Furthermore, the overlap of training folds between different runs induces implicit dependency in accuracy scores, which can violate the assumption of sample independence in many standard statistical tests [19].

Bootstrap Validation

Core Principle: Bootstrapping is a resampling technique that estimates the sampling distribution of a statistic by repeatedly drawing new samples (bootstrap samples) from the original dataset with replacement. This allows for the estimation of standard errors and confidence intervals.

Advanced Application: A fast bootstrap method has been developed to overcome the computational challenges of bootstrapping a CV estimate. This method quickly estimates the standard error of the cross-validation estimate and produces valid confidence intervals for a population parameter measuring average model performance by estimating the variance component within a random-effects model [31].

Experimental Comparison of CV and Bootstrap

Table 1: Comparison of Cross-Validation and Bootstrap Validation Characteristics

Characteristic Cross-Validation (K-fold) Bootstrap Validation
Core Principle Data splitting into K folds; iterative training and testing on different folds [19]. Resampling with replacement to create multiple simulated datasets [31].
Key Advantage Reduces optimism bias by enforcing training/testing separation [31]. Provides robust estimates of standard errors and confidence intervals [31].
Computational Cost Moderate (requires K model fits). Can be high, but efficient variants exist [31].
Statistical Stability Variance can be high with low K or small samples [19]. Generally provides stable performance estimates.
Uncertainty Quantification Challenging due to correlated estimates across folds [31] [19]. Naturally facilitates confidence interval estimation.
Optimal Use Case Model selection and hyperparameter tuning with limited data. Quantifying the robustness and reliability of a model's performance.

Experimental Data from Neuroimaging Studies

A recent study highlighted the practical challenges in quantifying the statistical significance of accuracy differences between two ML models when cross-validation is performed [19]. The study proposed an unbiased framework to assess the impact of CV setups on statistical significance and applied it to three neuroimaging datasets:

  • ADNI: Classifying Alzheimer's disease patients vs. healthy controls (N=444) [19].
  • ABIDE I: Distinguishing autism spectrum disorders from controls (N=849) [19].
  • ABCD: Identifying sex based on T1-weighted MRI (N=11,725) [19].

Table 2: Impact of CV Setup on Model Comparison Outcomes [19]

Dataset CV Configuration (K, M) Key Finding Implication
ABCD K=2, M=1 vs. K=50, M=10 Positive rate of detecting a significant difference increased by 0.49 on average. Likelihood of finding a "significant" model difference is highly sensitive to CV setup.
ABIDE Varying K and M Test sensitivity increased (lower p-values) with the number of CV repetitions M and the number of folds K. Risk of p-hacking; conclusions on model improvement can be inconsistent.
ADNI Varying K and M Despite applying two classifiers of the same intrinsic predictive power, the outcome of model comparison depended on CV setups. Questions the validity of model comparisons that do not account for this variability.

Interpretation: These findings underscore a critical flaw in common practices where a paired t-test is used to compare the two sets of K × M accuracy scores from two models. The study demonstrated that, even for two classifiers with the same intrinsic predictive power, the choice of K and M can lead to a higher likelihood of detecting a statistically significant accuracy difference, potentially leading to p-hacking and unreliable conclusions about model superiority [19].

Synthesized Decision Framework for Biomedical Applications

The following workflow synthesizes the evidence into a practical guide for selecting a validation method in biomedical research.

D Start Start: Biomedical Model Validation Need DataSize Dataset Size Assessment Start->DataSize SmallData Limited Sample Size (N < 500) DataSize->SmallData LargeData Adequate Sample Size (N >= 500) DataSize->LargeData Goal Primary Validation Goal SmallData->Goal Rec3 Recommendation: Hold-Out Validation\n(Single Train/Test Split) LargeData->Rec3 Goal1 Model Selection &\nHyperparameter Tuning Goal->Goal1 Goal2 Performance Robustness &\nUncertainty Quantification Goal->Goal2 Rec1 Recommendation: K-Fold Cross-Validation\n(K=5 or K=10) Goal1->Rec1 Rec2 Recommendation: Bootstrap Validation\n(or Repeated CV) Goal2->Rec2 Rec4 Recommendation: Fast Bootstrap\nfor CI Estimation Rec3->Rec4 For detailed uncertainty analysis

Detailed Framework Logic

  • Assess Dataset Size: The initial and most critical step is to evaluate the available sample size. In many biomedical settings, such as neuroimaging studies with N < 1000 [19], data can be limited.
  • For Limited Sample Sizes (N < 500): Proceed to define the primary goal of the validation.
    • If the goal is Model Selection & Tuning: Use K-Fold Cross-Validation (e.g., K=5 or K=10). This approach maximizes the use of limited data for both training and testing, providing a more reliable estimate of model performance than a single train/test split [19].
    • If the goal is Robustness & Uncertainty: Use Bootstrap Validation or Repeated Cross-Validation. These methods provide insights into the stability and variance of your performance metric [31].
  • For Adequate Sample Sizes (N >= 500): A simple Hold-Out Validation (a single train/validation/test split) is often sufficient and computationally efficient. For a more rigorous estimation of confidence intervals around model performance, the Fast Bootstrap method is recommended, as it overcomes computational challenges and provides valid confidence intervals [31].

Experimental Protocols

Protocol for K-Fold Cross-Validation with Model Comparison

This protocol is adapted from a framework used to evaluate neuroimaging-based classification models [19].

  • Data Preparation: Randomly shuffle the dataset and partition it into K folds of approximately equal size. For classification, ensure stratified folding to maintain class distribution.
  • Iterative Training and Testing: For each fold i (where i = 1 to K):
    • Designate fold i as the test set.
    • Combine the remaining K-1 folds to form the training set.
    • Train Model A and Model B on the identical training set.
    • Evaluate both models on the test set (fold i) and record the accuracy (or other relevant metrics) for each model.
  • Aggregation and Analysis: You will have K accuracy scores for Model A and K for Model B.
    • Incorrect Practice: Applying a paired t-test directly to these K paired scores, as they are not independent due to overlapping training data [19].
    • Recommended Practice: Use a corrected statistical test, such as the one described in [31] or a permutation test, that accounts for the dependencies introduced by the CV procedure. The fast bootstrap method [31] is also a viable option for quantifying the uncertainty of the CV estimate itself.

Protocol for Fast Bootstrap Cross-Validation Estimation

This protocol summarizes the computationally efficient method for estimating the uncertainty of a CV estimate [31].

  • Perform Standard K-fold CV: Execute the standard K-fold cross-validation procedure to obtain the initial performance estimate.
  • Variance Component Estimation: Instead of performing a full nested bootstrap (which is computationally prohibitive), the fast bootstrap method estimates the variance component within a random-effects model. This model accounts for both the variation due to the random splitting of the data and the variation inherent in the observed data itself.
  • Confidence Interval Construction: Using the estimated variance components, construct confidence intervals for the population parameter that measures the average model performance. This method is as flexible as the cross-validation procedure itself and does not require stringent model assumptions [31].

The Scientist's Toolkit: Essential Research Reagents

Table 3: Key Computational Tools and Concepts for Biomedical Validation

Item / Concept Function / Description Relevance to Framework
K-Fold Splitting A data partitioning strategy that creates K training/test splits to maximize data usage. Core to the CV method; essential for model tuning with limited data [19].
Bootstrap Resampling A technique that draws multiple samples with replacement from the original data to simulate sampling distribution. Core to the bootstrap method; allows for robust estimation of confidence intervals [31].
Stratified Sampling Ensures that each fold in CV maintains the same proportion of class labels as the full dataset. Crucial for validating classification models on imbalanced biomedical datasets.
Performance Metrics Quantifiable measures like accuracy, AUC, C-index, or mean absolute error. The outcome being validated; choice of metric should align with the biomedical question [31].
Statistical Test (Corrected) Hypothesis tests (e.g., corrected t-tests, permutation tests) designed for correlated CV results. Necessary for making statistically sound comparisons between models without inflated Type I error [19].
Fast Bootstrap Algorithm A specific computational method that efficiently estimates the standard error of a CV estimate. Recommended solution for quantifying uncertainty in CV without prohibitive computation [31].

Conclusion

Cross-validation and bootstrapping are both powerful, yet distinct, tools for internal validation. The choice between them is not one of superiority but of context. Cross-validation is generally preferred for model comparison and tuning in medium to large datasets, providing a good bias-variance tradeoff. In contrast, bootstrapping excels with small sample sizes and for estimating the uncertainty of model performance. For biomedical researchers, the key is to align the validation strategy with the research question, data structure, and intended use of the model. Future directions should focus on the adoption of more robust nested validation procedures, the development of standards for reporting validation results in clinical studies, and the integration of these techniques with emerging machine learning methods to build more reliable and generalizable predictive tools for personalized medicine and drug development.

References