From Theory to Therapy: The Historical Development of Computational Chemistry (1800-2015)

Abstract

This article traces the transformative journey of computational chemistry from its 19th-century theoretical foundations to its modern status as an indispensable tool in scientific research and drug development. It details the pivotal shift from a purely experimental science to one empowered by computer simulation, covering the inception of quantum mechanical theories, the birth of practical computational methods in the mid-20th century, and the rise of Nobel Prize-winning methodologies like Density-Functional Theory and multiscale modeling. Aimed at researchers and drug development professionals, the content explores key methodological advancements, persistent challenges in accuracy and scalability, the critical role of validation against experimental data, and the field's profound impact on rational drug design and materials science. By synthesizing historical milestones with current applications, this review provides a comprehensive resource for understanding how computational chemistry has reshaped the modern scientific landscape.

The Precursors to Computation: Laying the Theoretical Groundwork (1800-1940s)

This whitepaper examines the 19th-century Chemical Revolution through the dual lenses of atomic theory development and the systematic expansion of chemical space. By analyzing quantitative data on compound discovery from 1800-2015, we identify three distinct historical regimes in chemical exploration characterized by fundamental shifts in theoretical frameworks and experimental practices. The emergence of atomic theory provided the foundational paradigm that enabled structured navigation of chemical possibility, establishing principles that would later inform computational chemistry approaches. This historical analysis provides context for understanding the evolution of modern chemical research methodologies, particularly in pharmaceutical development where predictive molecular design is paramount.

The Chemical Revolution, traditionally dated to the late 18th century, represents a fundamental transformation in chemical theory and practice that established the modern science of chemistry [1]. While often associated primarily with Antoine Lavoisier's oxygen theory of combustion and his systematic approach to chemical nomenclature, this revolution extended well into the 19th century through the development and acceptance of atomic theory [1] [2]. The chemical revolution involved the rejection of phlogiston-based explanations of chemical phenomena in favor of empirical, quantitative approaches centered on the law of conservation of mass and the composition of compounds [2].

This period established the foundational principles that would eventually enable the emergence of computational chemistry centuries later. The systematic classification of elements and compounds, coupled with growing understanding of combination rules and reaction patterns, created the conceptual framework necessary for mathematical modeling of chemical systems [3]. Historical analysis reveals that the exploration of chemical space—the set of all possible molecules—has followed distinct, statistically identifiable regimes from the early 19th century to the present, with the 19th century establishing the essential patterns for subsequent chemical discovery [4].

Quantitative Analysis of Chemical Space Expansion

Analysis of millions of chemical reactions documented in the Reaxys database reveals clear patterns in the exploration of chemical space from 1800 to 2015 [4]. The annual number of new compounds reported grew exponentially at a stable 4.4% annual rate throughout this period, demonstrating remarkable consistency in the expansion of chemical knowledge despite major theoretical shifts and historical disruptions [4] [5].

Three Historical Regimes of Chemical Discovery

Statistical analysis identifies three distinct regimes in the exploration of chemical space, characterized by different growth rates and variability in annual compound output [4]:

Table 1: Historical Regimes in Chemical Space Exploration

Regime	Period	Annual Growth Rate (μ)	Standard Variation (σ)	Key Characteristics
Proto-organic	Before 1861	4.04%	0.4984	High variability in year-to-year output; mix of organic, inorganic, and metal-containing compounds
Organic	1861–1980	4.57%	0.1251	More regular production dominated by carbon- and hydrogen-containing compounds (>90% after 1880)
Organometallic	1981–2015	2.96%	0.0450	Revival of metal-containing compounds; most stable output variability

The transition between these regimes corresponds to major theoretical developments in chemistry. The shift from the proto-organic to organic regime around 1860 aligns with the widespread adoption of valence and structural theories, which enabled more systematic and predictable chemical exploration [4] [5]. This transition marks a movement from exploratory investigation to guided search within chemical space.

Impact of Major Historical Events

Analysis of the chemical discovery data reveals how major historical events affected the pace of chemical exploration [4]:

Table 2: Impact of World Wars on Chemical Discovery

Period	Annual Growth Rate	Contextual Factors
1914–1918 (WWI)	-17.95%	Significant disruption to chemical research
1919–1924 (Post-WWI)	18.98%	Rapid recovery and catch-up in chemical discovery
1940–1945 (WWII)	-6.00%	Moderate disruption, less severe than WWI
1946–1959 (Post-WWII)	12.11%	Sustained recovery and expansion

Remarkably, the long-term exponential growth trend continued despite these major disruptions, with the system returning to its baseline growth trajectory within approximately five years after each war [4] [5]. This resilience demonstrates the robustness of the chemical research enterprise once established patterns of investigation became institutionalized.

Foundations of Atomic Theory and Molecular Structure

The development of atomic theory provided the conceptual framework necessary for structured exploration of chemical space. John Dalton's atomic theory, introduced in the early 19th century, established several fundamental postulates that would guide chemical research for centuries [6] [7]:

• Elemental Atomic Uniqueness: Atoms of each element are identical in mass and properties and differ from atoms of all other elements [6]
• Compound Formation: Compounds form through the combination of atoms of different elements in fixed, small whole-number ratios [6] [7]
• Conservation in Reactions: Atoms are neither created nor destroyed in chemical reactions, only rearranged [6]

Dalton's theory provided a physical explanation for the Law of Multiple Proportions, which states that when two elements form more than one compound, the masses of one element that combine with a fixed mass of the other are in a ratio of small whole numbers [7]. This mathematical relationship between elements in compounds became a powerful predictive tool for exploring chemical space.

Experimental Foundations of Atomic Theory

Dalton's methodological approach established patterns for chemical investigation that would influence both experimental and later computational approaches:

Diagram 1: Dalton's Methodology for Atomic Theory Development

Dalton's experimental approach involved precise gravimetric measurements of elements combining to form compounds [7]. Despite limitations in his experimental technique and some incorrect molecular assignments (such as assuming water was HO rather than H₂O), his foundational insight that elements combine in fixed proportions provided the basis for calculating relative atomic masses and predicting new chemical combinations [7].

Experimental Protocols in 19th-Century Chemistry

Lavoisier's Combustion Experiments

Antoine Lavoisier's experimental work established new standards for precision measurement in chemistry and provided the empirical foundation for overturning phlogiston theory [1]:

Objective: Demonstrate that combustion involves combination with atmospheric components rather than release of phlogiston [1] [2]

Methodology:

• Precision Gravimetry: Conduct careful weighing of reactants and products before and after reactions using precision balances [1]
• Closed System Design: Utilize sealed apparatus to prevent mass loss or gain from the environment [1]
• Mercury Calx Experiment: Heat mercury in a sealed container to form mercury calx (oxide), noting the decreased air volume and increased solid mass [1]
• Gas Identification: Collect and characterize gases produced during reactions, identifying oxygen's role in combustion and respiration [1]
• Instrumentation: Employ thermometric and barometric measurements; collaborate in developing the calorimeter for heat measurement [1]

Key Reagents and Materials:

Table 3: Key Research Reagents in 19th Century Chemical Revolution

Reagent/Material	Chemical Formula	Primary Function in Experiments
Mercury (Hg)	Hg	Primary material in calx experiments demonstrating oxygen combination
Mercury Calx	HgO	Mercury oxide used to isolate oxygen upon decomposition
Oxygen	O₂	Isolated and identified as the active component in air supporting combustion
Hydrogen	H₂	Studied in combination reactions; used in water formation experiments
Water	H₂O	Decomposed and synthesized to demonstrate compound nature
Precision Balance	-	Gravimetric measurement for conservation of mass demonstrations
Calorimeter	-	Instrument for measuring heat changes in chemical reactions

Dalton's Atomic Weight Determinations

Objective: Establish relative weights of "ultimate particles" of elements through quantitative analysis of compound composition [7]

Methodology:

• Compound Selection: Identify binary compounds containing elements in simple combinations [7]
• Composition Analysis: Determine mass proportions of elements in compounds through decomposition or synthesis [7]
• Reference Standard: Establish hydrogen as reference atom with mass of 1 unit [7]
• Ratio Calculation: Compute relative masses of other elements based on combination ratios [7]
• Multiple Compound Analysis: Examine series of compounds containing the same elements to identify simple whole-number ratios [7]

Key Insight: The consistent appearance of small whole-number ratios in compound compositions provided primary evidence for discrete atomic combination [6] [7].

Theoretical Framework and Its Evolution

The 19th century witnessed the transition from phenomenological chemistry to theoretical frameworks with predictive capability. This evolution is visualized in the following conceptual map:

Diagram 2: Theoretical Evolution in 19th Century Chemistry

The Phlogiston to Oxygen Transition

The chemical revolution began with the rejection of phlogiston theory, which posited that combustible materials contained a fire-like element called phlogiston that was released during burning [2]. Lavoisier's systematic experiments demonstrated that combustion actually involved combination with oxygen, leading to the oxygen theory of combustion [1] [2]. This theoretical shift was significant because it replaced a qualitative, principle-based explanation with a quantitative, substance-based model that enabled precise predictions [2].

Structural Theory and Its Impact

The adoption of structural theory in the mid-19th century, including Kekulé's assignment of the cyclic structure to benzene and the development of valence theory, marked a critical turning point in chemical exploration [8]. This theoretical advancement enabled chemists to visualize molecular architecture and understand the spatial arrangement of atoms, dramatically increasing the efficiency of chemical synthesis and discovery [4]. The effect is visible in the quantitative data as a sharp reduction in the variability of annual compound output around 1860, indicating a transition from exploratory investigation to guided search within chemical space [4].

Bridge to Computational Chemistry

The theoretical and methodological foundations established during the 19th-century Chemical Revolution created the essential framework for the eventual development of computational chemistry in the 20th century [3]. The key connections include:

From Atomic Weights to Quantum Calculations

Dalton's relative atomic weights provided the first quantitative parameters for chemical prediction, establishing a tradition of numerical characterization that would evolve through Mendeleev's periodic law to modern quantum chemical calculations [7] [3]. The 20th century saw the implementation of these principles in computational methods:

• Early Computational Methods (1950s-1960s): The first semi-empirical atomic orbital calculations and ab initio Hartree-Fock methods applied quantum mechanics to molecular systems [3]
• Density Functional Theory (1960s-): Walter Kohn's development of density-functional theory demonstrated that molecular properties could be determined from electron density rather than wave functions [3] [9]
• Computational Software (1970s-): John Pople's development of the Gaussian program enabled practical quantum mechanical calculations for complex molecular systems [3] [9]

From Chemical Synthesis to Molecular Modeling

The 19th-century practice of systematic compound synthesis and characterization established the experimental data that would later train computational models [4] [3]. The exponential growth in characterized compounds documented in Reaxys and other chemical databases provides the essential reference data for validating computational chemistry predictions [4] [3].

Modern computational chemistry applies these historical principles to drug design and materials science, using quantum mechanical simulations to predict molecular behavior before synthesis [3] [9]. The 2013 Nobel Prize in Chemistry awarded to Levitt, Karplus, and Warshel for developing multiscale models of complex chemical systems represents the direct descendant of the methodological traditions established during the Chemical Revolution [9].

The 19th-century Chemical Revolution established the conceptual and methodological foundations that enabled the systematic exploration of chemical space. Through the development of atomic theory, structural understanding, and quantitative experimental approaches, chemists created a framework for navigating chemical possibility that would eventually evolve into computational chemistry. The exponential growth in chemical discovery documented from 1800 to 2015 demonstrates the remarkable productivity of this paradigm, while the identification of distinct historical regimes reveals how theoretical advances dramatically reshape research efficiency. For contemporary researchers in drug development and materials science, understanding this historical trajectory provides essential context for current computational approaches that build upon centuries of chemical investigation. The principles established during the Chemical Revolution continue to inform modern computational methodologies, creating an unbroken chain of chemical reasoning from Dalton's atomic weights to contemporary quantum simulations.

The period from 1800 to 2015 witnessed chemistry's transformation from an observational science to a predictive, computational discipline. This shift became possible only after theorists provided a mathematical description of matter at the quantum level. The pivotal breakthrough came in 1926, when Erwin Schrödinger published his famous wave equation, creating a mathematical foundation for describing the behavior of electrons in atoms and molecules [10] [11]. This equation, now fundamental to quantum mechanics, gave chemists an unprecedented tool: the ability to calculate molecular properties from first principles rather than relying solely on experimental measurement [10] [3].

Schrödinger's equation is the quantum counterpart to Newton's second law in classical mechanics, predicting the evolution over time of the wave function (Ψ), which contains all information about a quantum system [10]. The discovery that electrons could be described as waves with specific probability distributions meant that chemists could now computationally model atomic structure and chemical bonding [11]. This quantum leap created the foundation for computational chemistry, a field that uses computer simulations to solve chemical problems that are often intractable through experimental methods alone [3]. The subsequent development of computational chemistry represents one of the most significant paradigm shifts in the history of chemical research, enabling scientists to explore chemical space—the totality of possible molecules—through simulation rather than solely through laboratory synthesis [5] [4].

Historical Backdrop: Chemical Discovery from 1800-2015

The exponential growth of chemical knowledge from 1800 to 2015 provides crucial context for understanding Schrödinger's revolutionary impact. Analysis of millions of compounds recorded in chemical databases reveals distinct eras of chemical discovery, each characterized by different approaches and theoretical understandings [4].

Table 1: Historical Regimes in Chemical Discovery (1800-2015)

Regime	Time Period	Annual Growth Rate	Key Characteristics
Proto-organic	1800-1860	4.04%	High variability in annual compound discovery; mix of organic and metal-containing compounds; early synthetic chemistry
Organic	1861-1980	4.57%	More regular discovery pace; carbon- and hydrogen-containing compounds dominated (>90% after 1880); structural theory guided synthesis
Organometallic	1981-2015	2.96%-4.40%	Most consistent discovery rate; revival of metal-containing compounds; computational methods increasingly important

Analysis of the Reaxys database containing over 14 million compounds reported between 1800 and 2015 demonstrates that chemical discovery grew at a remarkable 4.4% annual rate over this 215-year period [5] [4]. This exponential growth was surprisingly resilient, continuing through World Wars despite temporary dips, with recovery to pre-war discovery rates within five years after each conflict [4]. What changed fundamentally with Schrödinger's contribution was not the pace of discovery, but the methodology—providing a theoretical framework that would eventually enable predictive computational chemistry rather than purely empirical approaches.

The Schrödinger Equation: Mathematical Foundation

Core Theoretical Principles

The Schrödinger equation is a partial differential equation that governs the wave function of a quantum-mechanical system [10]. Its time-dependent form is:

iℏ(∂/∂t)|Ψ(t)⟩ = Ĥ|Ψ(t)⟩

where i is the imaginary unit, ℏ is the reduced Planck constant, |Ψ(t)⟩ is the quantum state vector (wave function) of the system, and Ĥ is the Hamiltonian operator corresponding to the total energy of the system [10]. For many practical applications in chemistry, the time-independent form is used:

Ĥ|Ψ⟩ = E|Ψ⟩

where E is the energy eigenvalue corresponding to the stationary state |Ψ⟩ [10]. Solving this eigenvalue equation provides both the wave function, which describes the probability distribution of electrons, and the associated energy levels of the system [12].

The Hamiltonian operator consists of two fundamental components: the kinetic energy of all particles in the system and the potential energy arising from their interactions [12]. For chemical systems, this typically includes electron kinetic energy, electron-nucleus attraction, and electron-electron repulsion. The complexity of solving the Schrödinger equation increases dramatically with the number of particles in the system, giving rise to the many-body problem that necessitates computational approaches for all but the simplest chemical systems [3].

From Equation to Atomic Model

Schrödinger's critical innovation was applying wave equations to describe electron behavior in atoms, representing a radical departure from previous planetary models of the atom [11]. His model assumed the electron behaves as a wave and described regions in space (orbitals) where electrons are most likely to be found [11]. Unlike Niels Bohr's earlier one-dimensional model that used a single quantum number, Schrödinger's three-dimensional model required three quantum numbers to describe atomic orbitals: the principal (n), angular (l), and magnetic (m) quantum numbers, which describe orbital size, shape, and orientation [11].

This wave-mechanical approach fundamentally changed how chemists conceptualized electrons—abandoning deterministic trajectories for probabilistic distributions [11]. The Schrödinger model no longer told chemists precisely where an electron was at any moment, but rather where it was most likely to be found, represented mathematically by the square of the wave function |Ψ|² [13] [11]. This probabilistic interpretation formed the crucial link between abstract mathematics and chemically meaningful concepts like atomic structure and bonding.

The Computational Framework: From Equation to Application

Implementing the Schrödinger Equation in Chemistry

Applying the Schrödinger equation to chemical systems involves constructing an appropriate Hamiltonian operator for the system of interest, then solving for the wave functions and corresponding energies [12]. The process follows a systematic methodology:

The Hamiltonian operator (Ĥ) is built from the kinetic energy of all particles (electrons and nuclei) and the potential energy of their interactions (electron-electron repulsion, electron-nucleus attraction, and nucleus-nucleus repulsion) [12]. For a molecular system, this becomes extraordinarily complex due to the many interacting particles, necessitating the Born-Oppenheimer approximation, which separates nuclear and electronic motion based on their mass difference [13]. This approximation simplifies the problem by treating nuclei as fixed while solving for electron distribution, making computational solutions feasible [13].

Computational Methodologies and Approximations

As computational chemistry evolved, distinct methodological approaches emerged to solve the Schrödinger equation with varying balances of accuracy and computational cost:

Table 2: Computational Chemistry Methods for Solving the Schrödinger Equation

Method Class	Key Approximations	Accuracy vs. Cost	Typical Applications
Ab Initio	No empirical parameters; begins directly from theoretical principles	High accuracy, high computational cost	Small to medium molecules; benchmark calculations
Hartree-Fock	Approximates electron-electron repulsion with average field	Moderate accuracy, high cost for large systems	Basis for post-Hartree-Fock methods
Density Functional Theory (DFT)	Uses electron density rather than wave function	Good accuracy with reasonable cost	Large molecules; solids and surfaces
Semi-empirical	Incorporates empirical parameters to simplify calculations	Lower accuracy, lower cost	Very large systems; initial screening

The Hartree-Fock method represents a fundamental approach that approximates the many-electron wave function as a Slater determinant of single-electron orbitals [3]. While it provides a starting point for more accurate calculations, its neglect of electron correlation (the instantaneous repulsion between electrons) limits its accuracy [3]. Post-Hartree-Fock methods like configuration interaction, coupled cluster theory, and perturbation theory introduce electron correlation corrections, improving accuracy at increased computational expense [3].

The development of Density Functional Theory (DFT) provided a revolutionary alternative by using electron density rather than wave functions as the fundamental variable, significantly reducing computational complexity while maintaining good accuracy for many chemical applications [3]. This breakthrough, for which Walter Kohn received the Nobel Prize in 1998, made calculations on larger molecules practically feasible and became one of the most widely used methods in computational chemistry [3].

Modern computational chemistry relies on specialized software tools and databases that implement methods for solving the Schrödinger equation across diverse chemical systems:

Table 3: Essential Resources for Computational Chemistry Research

Resource Type	Examples	Primary Function	Role in Schrödinger Equation Applications
Software Platforms	Gaussian, Schrödinger Maestro, ATMO	Implement computational methods	Provide algorithms for solving electronic structure equations
Chemical Databases	Reaxys, BindingDB, RCSB, ChEMBL	Store chemical structures and properties	Provide experimental data for method validation
Quantum Chemistry Packages	GAMESS, NWChem, ORCA	Perform ab initio calculations	Specialize in wave function-based electronic structure methods
Visualization Tools	Maestro, PyMOL	Represent molecular structures and orbitals	Translate wave function data into visual atomic models

These tools enable researchers to apply the Schrödinger equation to practical chemical problems without developing computational methods from scratch. For example, the Schrödinger computational platform provides integrated tools for molecular modeling, visualization, and prediction of molecular properties, allowing researchers to bring "molecules to life on the computer" by accurately simulating properties that would otherwise require laboratory experimentation [14].

Databases play a crucial role in both validating computational methods and providing starting points for further exploration. The Reaxys database, containing millions of compounds and reactions, has been instrumental in tracing the historical development of chemical discovery and provides essential reference data for comparing computational predictions with experimental results [5] [4].

Applications and Impact: Transforming Chemical Research

Drug Design and Development

Computational chemistry has revolutionized pharmaceutical research by enabling the prediction of drug-target interactions without synthesizing every candidate compound [14]. For example, recent applications have demonstrated the ability to explore over 1 billion molecules computationally to design new inhibitors for therapeutic targets like d-amino acid oxidase (DAO) for schizophrenia treatment [14]. This approach combines quantum mechanics with machine learning to screen vast chemical spaces rapidly, accelerating the lead optimization process that traditionally required extensive laboratory work [14].

The integration of active learning with physics-based molecular docking represents another significant advancement, allowing researchers to test approximately 30,000 compounds per second compared to traditional computational methods that process about one compound every 30 seconds—a 10,000-fold speed increase [14]. This dramatic acceleration enables pharmaceutical researchers to explore chemical space more comprehensively while focusing synthetic efforts on the most promising candidates.

Materials Science and Industrial Applications

Beyond pharmaceuticals, computational chemistry methods have transformed materials design across multiple industries. In consumer packaged goods, companies like Reckitt use quantum mechanics and molecular dynamics simulations to design more sustainable materials, reportedly speeding development timelines by 10x on average compared to purely experimental approaches [14].

In energy research, atomic-scale modeling facilitates the design of improved battery technologies by simulating ion diffusion, electrochemical responses in electrodes and electrolytes, dielectric properties, and mechanical responses [14]. These computational approaches enable the screening of Li-ion battery additives that form stable solid electrolyte interfaces, a crucial factor in battery performance and longevity [14].

Catalysis represents another area where computational chemistry has made significant contributions. Modern electronic structure theory and density functional theory allow researchers to understand catalytic systems without extensive experimentation, predicting values like activation energy, site reactivity, and thermodynamic properties that guide catalyst design [3]. Computational studies provide insights into catalytic mechanisms that are difficult to observe experimentally, enabling the development of more efficient and selective catalysts for industrial applications [3].

Current Status and Future Directions

The field of computational chemistry continues to evolve, with ongoing developments in both methodological sophistication and computational infrastructure. The integration of machine learning with physics-based methods represents the current frontier, combining the accuracy of first-principles calculations with the speed of data-driven approaches [14]. This synergy addresses the fundamental trade-off between computational cost and accuracy that has constrained the application of quantum chemical methods to very large systems [14].

The historical analysis of chemical discovery suggests that we are currently in the organometallic regime, characterized by decreased variability in annual compound output and the rediscovery of metal-containing compounds [5] [4]. This era has also seen computational chemistry become fully integrated into the chemical research enterprise, with several Nobel Prizes recognizing contributions to the field, including the 1998 award to Walter Kohn and John Pople and the 2013 award to Martin Karplus, Michael Levitt, and Arieh Warshel for developing multiscale models for complex chemical systems [3].

As computational power continues to grow and algorithms become more sophisticated, the applications of Schrödinger's equation in chemistry will expand further, potentially enabling fully predictive molecular design across increasingly complex chemical and biological systems. This progression continues the quantum leap that began nearly a century ago, transforming chemistry from a primarily observational science to a computational and predictive one, fundamentally expanding our ability to explore chemical space and design novel molecules with desired properties.

The year 1927 marked a seminal moment in the history of theoretical chemistry, as Walter Heitler and Fritz London provided the first successful quantum mechanical treatment of the hydrogen molecule (H₂). This groundbreaking work, emerging just one year after Erwin Schrödinger published his wave equation, laid the foundational principles for understanding the covalent bond and established the cornerstones of what would later evolve into the field of computational chemistry [15] [16] [3]. Their approach, now known as the Heitler-London (HL) model or the valence bond method, demonstrated that chemical bonding could be understood through the application of quantum mechanics, moving beyond classical descriptions to explain the stability, bond length, and binding energy of molecules from first principles [17] [3].

The broader historical development of chemistry from 1800 to 2015 is characterized by exponential growth in the discovery of new compounds, with an annual growth rate of approximately 4.4% over this period [4]. This exploration of chemical space has transitioned through three distinct historical regimes: a proto-organic regime (before ~1860) with high variability in annual output, a more structured organic regime (approx. 1861-1980), and the current organometallic regime (approx. 1981-present) characterized by decreasing variability and more regular production [4]. The HL model emerged during the organic regime, providing the theoretical underpinnings for understanding molecular structure and bonding that would fuel further chemical discovery. The development of computational chemistry as a formal discipline represents a natural evolution from these early theoretical foundations, bridging the gap between chemical theory and the prediction of chemical phenomena.

The Heitler-London Model: Theoretical Foundations

The Quantum Mechanical Framework

The Heitler-London approach addressed the fundamental challenge of describing a four-particle system: two protons and two electrons. Within the Born-Oppenheimer approximation, which decouples nuclear and electronic motion due to the significant mass difference, the electronic Hamiltonian for the H₂ molecule in atomic units is given by [17] [16]:

$$ \hat{H} = -\frac{1}{2}{\nabla}1^{2} -\frac{1}{2}{\nabla}2^{2} -\frac{1}{r{1A}} -\frac{1}{r{1B}} -\frac{1}{r{2A}} -\frac{1}{r{2B}} +\frac{1}{r_{12}} +\frac{1}{R} $$

Table 1: Components of the Hydrogen Molecule Hamiltonian

Term	Physical Significance
$-\frac{1}{2}\nabla1^2 -\frac{1}{2}\nabla2^2$	Kinetic energy of electrons 1 and 2
$-\frac{1}{r{1A}} -\frac{1}{r{1B}} -\frac{1}{r{2A}} -\frac{1}{r{2B}}$	Attractive potential between electrons and protons
$\frac{1}{r_{12}}$	Electron-electron repulsion
$\frac{1}{R}$	Proton-proton repulsion

The coordinates refer to the two electrons (1,2) and two protons (A,B), with $r{ij}$ representing the distance between particles $i$ and $j$, and $R$ the internuclear separation [16]. The complexity of this system lies in the electron-electron correlation term ($1/r{12}$), which prevents an exact analytical solution.

The Wave Function Ansatz

The key insight of Heitler and London was to construct a molecular wave function from a linear combination of atomic orbitals. For the hydrogen molecule, they proposed using the 1s orbitals of isolated hydrogen atoms:

$$ \phi(r{ij}) = \sqrt{\frac{1}{\pi}} e^{-r{ij}} $$

where $\phi(r{ij})$ represents the 1s orbital for an electron at a distance $r{ij}$ from a proton [16]. The molecular wave function was then expressed as:

$$ \psi{\pm}(\vec{r}1,\vec{r}2) = N{\pm} [\phi(r{1A})\phi(r{2B}) \pm \phi(r{1B})\phi(r{2A})] $$

where $N_{\pm}$ is the normalization constant [16]. This wave function satisfies the fundamental requirement that as $R \to \infty$, it properly describes two isolated hydrogen atoms.

Bonding and Antibonding States

The symmetric ($\psi+$) and antisymmetric ($\psi-$) combinations of atomic orbitals give rise to bonding and antibonding states, respectively. When combined with the appropriate spin functions, these yield the singlet and triplet states of the hydrogen molecule [16]:

• Singlet State (Bonding): $\Psi{(0,0)}(\vec{r}1,\vec{r}2) = \psi+(\vec{r}1,\vec{r}2)\frac{1}{\sqrt{2}}(|\uparrow\downarrow\rangle - |\downarrow\uparrow\rangle)$
• Triplet State (Antibonding): $\Psi{(1,1)}(\vec{r}1,\vec{r}2) = \psi-(\vec{r}1,\vec{r}2)|\uparrow\uparrow\rangle$, etc.

The bonding state corresponds to the electrons being spatially closer to both nuclei with opposite spins, resulting in a lower energy than two separated hydrogen atoms, thereby explaining the covalent bond formation [15] [16].

Figure 1: Theoretical workflow of the Heitler-London model showing the derivation of molecular states from atomic orbitals

Methodologies and Computational Approaches

Original Heitler-London Calculation Protocol

The original HL methodology followed a well-defined protocol for calculating molecular properties:

• Wave Function Construction: Define the trial wave function as a linear combination of hydrogen 1s atomic orbitals as shown in Section 2.2.

• Energy Calculation: Compute the total energy as a function of internuclear distance R using the variational integral: $$ \tilde{E}(R) = \frac{\int{\psi \hat{H} \psi d\tau}}{\int{\psi^2 d\tau}} $$ where $\hat{H}$ is the molecular Hamiltonian [17].

• Energy Components: The total energy calculation involves determining several integrals representing:

  • Coulomb integrals ($Q$) representing the energy of electron density around one nucleus interacting with the other nucleus
  • Exchange integrals ($J$) representing the quantum mechanical exchange interaction
  • Overlap integrals ($S$) measuring the spatial overlap of atomic orbitals

• Optimization: Find the equilibrium bond length ($Re$) by identifying the minimum in the $E(R)$ curve, and calculate the binding energy ($De$) as the energy difference between the minimum and the dissociated atoms [17].

Modern Computational Refinements

Recent work by da Silva et al. (2025) has extended the original HL model by incorporating electronic screening effects [15] [16]. Their methodology includes:

• Screening Modification: Introducing a variational parameter $\alpha(R)$ as an effective nuclear charge that accounts for how electrons screen each other from the nuclear attraction: $$ \phi(r{ij}) = \sqrt{\frac{\alpha^3}{\pi}} e^{-\alpha r{ij}} $$ where $\alpha$ is optimized as a function of $R$ [16].

• Variational Quantum Monte Carlo (VQMC): Using stochastic methods to optimize the screening parameter and evaluate expectation values of the Hamiltonian with high accuracy, accounting for electron correlation effects beyond the mean-field approximation [15] [16].

• Parameter Optimization: Determining $\alpha(R)$ by minimizing the energy with respect to this parameter at each internuclear separation, resulting in a function that describes how screening changes during bond formation and dissociation [16].

Table 2: Research Reagent Solutions – Computational Tools

Computational Tool	Function/Role	Theoretical Basis
Hydrogen 1s Atomic Orbitals	Basis functions for molecular wave function	$\phi(r) = \sqrt{\frac{1}{\pi}} e^{-r}$ [16]
Variational Principle	Energy optimization method	$\tilde{E} = \frac{\int{\psi \hat{H} \psi d\tau}}{\int{\psi^2 d\tau}}$ [17]
Effective Nuclear Charge ($\alpha$)	Accounts for electronic screening	Modified orbital: $\phi(r) = \sqrt{\frac{\alpha^3}{\pi}} e^{-\alpha r}$ [16]
Quantum Monte Carlo	Stochastic evaluation of integrals	Uses random sampling for high-accuracy correlation energy [15]

Quantitative Results and Comparison

Molecular Properties of H₂

The Heitler-London model yielded quantitative predictions for the hydrogen molecule that, while approximate, captured the essential physics of the covalent bond:

Table 3: Comparison of H₂ Molecular Properties Across Computational Methods

Method	Bond Length (Å)	Binding Energy (eV)	Vibrational Frequency (cm⁻¹)
Original HL Model (1927)	~0.90 [17]	~0.25 [17]	Not reported
Screening-Modified HL (2025)	~0.74 [16]	Improved agreement	Improved agreement
Experimental	0.7406 [17]	4.746 [17]	4401

The original HL calculation obtained a binding energy of approximately 3.14 eV (0.25 eV according to [17]) and an equilibrium bond length of about 1.7 bohr (~0.90 Å), which, while qualitatively correct, significantly underestimated the actual binding strength of the molecule [17] [16]. The screening-modified HL model shows substantially improved agreement with experimental values, particularly for the bond length [16].

Energy Components and Potential Curves

The HL model decomposes the molecular energy into physically interpretable components:

• Coulomb Integral (Q): Represents the classical electrostatic interaction between the charge distributions of two hydrogen atoms.

• Exchange Integral (J): A purely quantum mechanical term arising from the indistinguishability of electrons, responsible for the energy splitting between bonding and antibonding states.

• Overlap Integral (S): Measures the spatial overlap between atomic orbitals, influencing the normalization and strength of interaction.

The potential energy curve obtained from the original HL calculation shows the characteristic shape of a molecular bond: repulsive at short distances, a minimum at the equilibrium bond length, and asymptotic approach to the separated atom limit at large R [17]. The screening-modified model produces a potential curve with a deeper well and minimum at shorter bond lengths, in better agreement with high-precision calculations and experimental data [16].

Figure 2: Computational workflow for the screening-modified Heitler-London calculation

Historical Significance and Modern Context

Foundation of Computational Chemistry

The Heitler-London model represents the pioneering effort in what would become the field of computational chemistry. Their 1927 calculation marks the first successful application of quantum mechanics to a molecular system, establishing several fundamental concepts [3]:

• Covalent Bond Explanation: Provided the first quantum mechanical explanation of the covalent bond as arising from electron sharing between atoms.

• Valence Bond Theory: Established the basic principles of valence bond theory, which would compete with molecular orbital theory for describing chemical bonding.

• Quantum Chemistry Methodology: Introduced the conceptual and methodological framework for performing quantum chemical calculations on molecules.

The historical development of computational chemistry from this foundation can be traced through several key advancements: the early semi-empirical methods of the 1950s, the development of ab initio Hartree-Fock methods, the introduction of density functional theory by Kohn in the 1960s, and the emergence of sophisticated computational packages like Gaussian [3]. The field was formally recognized with Nobel Prizes in 1998 to Walter Kohn and John Pople, and in 2013 to Martin Karplus, Michael Levitt, and Arieh Warshel for developing multiscale models for complex chemical systems [9] [3].

Contemporary Applications and Relevance

The legacy of the Heitler-London approach continues in modern computational chemistry, particularly in drug development and materials science [3]:

• Drug Design: Computational methods derived from these quantum mechanical principles are used to model drug-receptor interactions, predict binding affinities, and optimize pharmaceutical compounds before synthesis [3].

• Catalysis Research: Computational chemistry enables the analysis of catalytic systems without extensive experimentation, predicting activation energies and reaction pathways for catalyst design [3].

• Materials Science: The principles established in the HL model underpin calculations of electronic structure, band gaps, and properties of novel materials [3].

• Quantum Chemistry Software: Modern computational packages (Gaussian, GAMESS, VASP) implement advanced methods that remain conceptually indebted to the HL approach [3].

The exponential growth in chemical discovery documented from 1800 to 2015, with distinct regimes of chemical exploration, has been accelerated by these computational approaches [4]. The transition from the proto-organic to organic regime around 1860 coincided with the development of structural theory, while the current organometallic regime (post-1980) benefits from sophisticated computational design methods rooted in the quantum mechanical principles first established by Heitler and London [4].

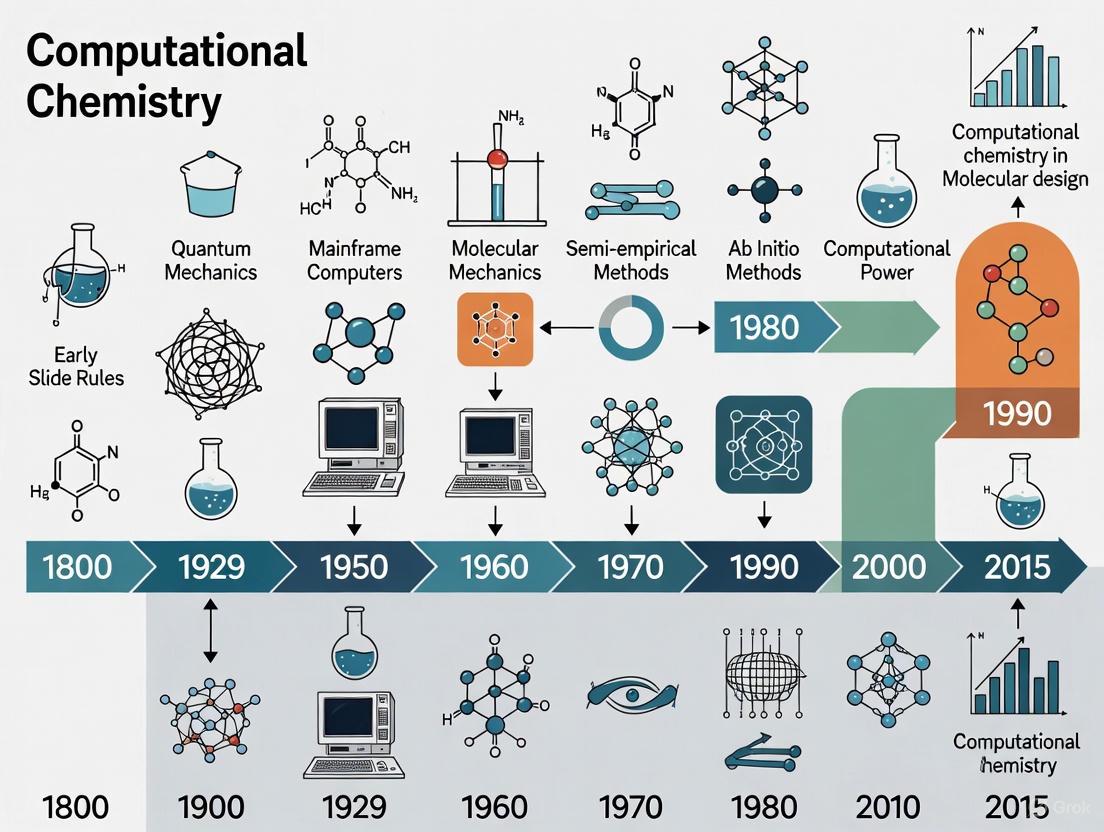
The period preceding the advent of digital computers established the foundational theoretical frameworks and calculational techniques that would later enable the emergence of computational chemistry as a formal discipline. This era was characterized by the development of mathematical descriptions of chemical systems and the ingenious application of manual approximation methods to solve complex quantum mechanical equations. Chemists and physicists devised strategies to simplify the many-body problem inherent in quantum systems, making calculations tractable with the available tools—primarily pencil, paper, and mechanical calculators. These early efforts were crucial for building the conceptual infrastructure that would later be encoded into computer programs, allowing for the quantitative prediction of molecular structures, properties, and reaction paths [3]. The work of this period, though computationally limited by modern standards, provided the essential theories and validation needed for the subsequent exponential growth of chemical knowledge [4].

Historical Context and the Growth of Chemical Knowledge (1800-1950)

The exploration of chemical space long preceded the formal establishment of computational chemistry. Analysis of historical data reveals that the reporting of new chemical compounds grew at an exponential rate of approximately 4.4% annually from 1800 to 2015, a trend remarkably stable through World Wars and scientific revolutions [4]. This exploration occurred through three distinct historical regimes, the first two of which fall squarely within the pre-computer era.

• The Proto-Organic Regime (pre-1860): This period was characterized by high variability in the year-to-year output of new compounds, with an annual growth rate of approximately 4.04%. Chemistry during this era focused on the extraction and analysis of animal and plant products alongside inorganic compounds. Contrary to common belief, synthesis was already a key provider of new compounds well before Friedrich Wöhler's 1828 synthesis of urea, though the methods were not yet systematic or guided by a unified structural theory [4].
• The Organic Regime (1861-1980): The establishment of structural theory around 1860 marked a sharp transition to a period of more regular and guided chemical production, with an annual growth rate of 4.57%. This theory provided a conceptual map for chemical space, enabling chemists to plan syntheses more rationally and leading to a significant decrease in the variability of chemical output [4]. The dominance of carbon-, hydrogen-, nitrogen-, oxygen-, and halogen-based compounds solidified during this period.

The following table summarizes the key characteristics of these historical regimes, highlighting the shifting patterns of chemical exploration during the pre-computer and early computer eras [4].

Table 1: Historical Regimes in the Exploration of Chemical Space

Regime	Period	Annual Growth Rate (μ)	Key Characteristics
Proto-Organic	Before 1861	4.04%	High variability; extraction from natural sources; early synthesis; no unifying structural theory.
Organic	1861–1980	4.57%	Guided by structural theory; decreased variability; dominance of organic molecules.
Organometallic	1981–2015	2.96%	Rise of organometallic compounds; lowest variability; enabled by advanced computational modeling.

The scientist's toolkit evolved significantly throughout these regimes. The following table details the most frequently used chemical reagents during various sub-periods, illustrating the changing focus and available materials for experimental and theoretical work [4].

Table 2: Evolution of Key Research Reagents (Top 3 by Period)

Period	Top Reagents
Before 1860	H₂O, NH₃, HNO₃
1860-1879	H₂O, HCl, H₂SO₄
1880-1899	HCl, EtOH, H₂O
1900-1919	EtOH, HCl, AcOH

Foundational Theoretical Frameworks

The pre-computer era was marked by the development of several pivotal theoretical frameworks that provided the mathematical foundation for describing chemical systems.

The Birth of Quantum Chemistry

The first theoretical chemistry calculations stemmed directly from the founding discoveries of quantum mechanics. A landmark achievement was the 1927 work of Walter Heitler and Fritz London, who applied valence bond theory to the hydrogen molecule. This represented the first successful quantum mechanical treatment of a chemical bond, demonstrating that the stability of the molecule could be explained through the wave-like nature of electrons and their linear combination [3] [9]. This work proved that chemical bonding could be understood through the application of quantum theory, paving the way for a more rigorous and predictive theoretical chemistry.

The Born-Oppenheimer Approximation

Introduced in 1927, the Born-Oppenheimer approximation became a cornerstone of quantum chemistry. This approximation simplifies the molecular Schrödinger equation by exploiting the significant mass difference between electrons and nuclei. It posits that due to their much heavier mass, nuclei move much more slowly than electrons. Consequently, the motion of the nuclei and electrons can be treated separately: the electrons can be considered as moving in a field of fixed nuclei [18]. This separation reduces the complexity of the problem dramatically. For example, the benzene molecule (12 nuclei and 42 electrons) presents a partial differential eigenvalue equation in 162 variables. The Born-Oppenheimer approximation allows this to be separated into a more manageable form, making hand-calculation of electronic structure for small systems feasible [18].

The Hartree Method and the Self-Consistent Field

Developed by Douglas Hartree in 1928, the Hartree method was a crucial step towards tackling multi-electron systems. The fundamental challenge is the electron-electron repulsion term in the Hamiltonian, which couples the motions of all electrons and makes the Schrödinger equation unsolvable without approximation. Hartree's key insight was to assume that each electron moves in an averaged potential created by the nucleus and the cloud of all other electrons [18]. This effective potential depends only on the coordinates of the single electron in question. The solution is found iteratively: an initial guess for the wavefunctions is made, the potential is calculated, and new wavefunctions are solved for. This process is repeated until the wavefunctions and potential become consistent, hence the name Self-Consistent Field (SCF) method. While this method neglected the fermionic nature of electrons (later corrected by Fock and Slater), it established the core SCF procedure that remains central to electronic structure calculations today.

Key Hand-Calculated Approximation Methods

With the theoretical frameworks in place, chemists developed specific approximation methods to perform practical calculations.

The Hückel Method

Proposed by Erich Hückel in the 1930s, Hückel Molecular Orbital (HMO) theory was a semi-empirical method designed to provide a qualitative, and later semi-quantitative, understanding of the π-electron systems in conjugated hydrocarbons. Its power lay in its drastic simplifications, which made hand-calculation of molecular orbital energies and wavefunctions possible for relatively large organic molecules [3]. The method's approximations include:

• σ-π Separation: The π-electrons are treated independently from the σ-framework, which is considered a rigid core.
• Differential Overlap Neglect: Certain integrals in the secular equations are set to zero.
• Parameterization: The Hamiltonian matrix elements are replaced with empirical parameters: the Coulomb integral (α) for the energy of an electron in a 2p orbital, and the resonance integral (β) for the interaction energy between two adjacent 2p orbitals [3].

By the 1960s, researchers were using computers to perform Hückel method calculations on molecules as complex as ovalene, but the method was originally designed for and successfully applied through manual calculation [3].

Semi-Empirical Methods

The need for more quantitative accuracy than Hückel theory could provide, while still avoiding the computational intractability of ab initio methods, led to the development of more sophisticated semi-empirical methods in the 1960s, such as CNDO (Complete Neglect of Differential Overlap) [3]. These methods retained the core LCAO (Linear Combination of Atomic Orbitals) formalism of Hartree-Fock theory but made further approximations. They neglected certain classes of two-electron integrals and parameterized others based on experimental data (e.g., ionization potentials, electron affinities). This approach incorporated some of the effects of electron correlation empirically, yielding results that were more accurate than simple Hückel theory and could be applied to a wider range of molecules, though they still largely depended on manual setup and calculation before the widespread use of digital computers.

Methodologies for Early Calculations

The workflow for theoretical calculations in the pre-computer era was meticulous and labor-intensive, requiring a deep understanding of both the chemical system and the mathematical tools.

The Linear Combination of Atomic Orbitals (LCAO) Approach

The LCAO approach forms the basis for most molecular orbital calculations. The methodology involves several key steps that were executed manually [3] [18]:

• Basis Set Selection: The calculation begins by selecting a set of atomic orbitals (the basis set) for each atom in the molecule. In early hand calculations, these were typically Slater-type orbitals (STOs) or minimal sets of hydrogen-like orbitals.
• Construction of the Secular Equation: The molecular orbitals are written as linear combinations of the chosen atomic orbitals. This leads to the formulation of the secular equation: H - ES = 0, where H is the Hamiltonian matrix, E is the orbital energy, and S is the overlap matrix.
• Matrix Element Calculation: The matrix elements of H and S are calculated based on the chosen approximation level (e.g., Hückel, semi-empirical). This often involved consulting tables of integrals and applying empirical parameters.
• Solving the Secular Determinant: The secular equation is solved by finding the roots of the secular determinant |H - ES| = 0. This yields the orbital energies (E). For a molecule with N basis functions, this is an N-th order polynomial equation.
• Determination of Molecular Orbitals: For each orbital energy, the coefficients in the LCAO expansion are determined by solving a system of linear equations. These coefficients define the shape and nodal structure of each molecular orbital.
• Electron Assignment and Property Calculation: Electrons are assigned to the molecular orbitals according to the Aufbau principle and Hund's rule. Finally, total electron density, bond orders, and other properties are derived from the occupied orbitals.

Workflow for a Hückel Calculation

The following diagram illustrates the logical workflow and key decision points for performing a hand-calculated Hückel method study of a conjugated molecule.

Limitations and Challenges of Pre-Computer Calculations

Theoretical work in the pre-computer era was fundamentally constrained by the tools available. The primary challenge was the exponential scaling of computational effort with system size. Solving the secular determinant for a molecule with N basis functions involved finding the roots of an N-th order polynomial, a task that becomes prohibitively difficult for all but the smallest molecules as N increases. This severely limited the size and complexity of molecules that could be practically studied. Polyatomic molecules with more than a few heavy atoms were largely beyond reach for all but the most approximate methods like Hückel theory [3].

Furthermore, the neglect of electron correlation was a major source of inaccuracy. Methods like Hartree-Fock and Hückel theory treated electrons as moving in an average field, ignoring the correlated nature of their instantaneous repulsions. This led to systematic errors in predicting properties like bond dissociation energies and reaction barriers. While post-Hartree-Fock methods like Configuration Interaction (CI) were developed conceptually in the 1950s, they were computationally intractable for any meaningful chemical system without electronic computers [3]. The lack of computing power also meant that relativistic effects were almost entirely neglected, limiting accurate quantum chemical descriptions to elements in the first few rows of the periodic table [18].

The pre-computer era of theoretical chemistry was a period of profound intellectual achievement. Despite being limited to manual calculations, chemists and physicists established the core principles that would define the field: the application of quantum mechanics to chemical systems, the development of critical approximations like Born-Oppenheimer, and the creation of tractable computational models like the Hartree-Fock method and Hückel theory. The exponential growth of chemical knowledge during the Organic regime (1861-1980) was, in part, enabled by these theoretical frameworks, which provided a guided, rational approach to exploring chemical space [4]. The painstaking hand-calculations of this period not only solved specific chemical problems but also validated the underlying theories, creating a solid foundation. When digital computers finally became available in the latter half of the 20th century, this well-established conceptual framework was ready to be translated into code, launching computational chemistry as a formal discipline and unlocking the potential for the accurate modeling of complex chemical systems.

The Computing Revolution: Key Methodologies and Their Transformative Applications

The period from the 1950s to the 1960s marked a revolutionary epoch in chemistry, characterized by the transition from purely theoretical mathematics to practical computational experimentation. This era witnessed the birth of computational chemistry as a distinct discipline, enabled by the advent of digital computers that provided the necessary tools to obtain numerical approximations to the solution of the Schrödinger equation for chemical systems [19]. Prior to these developments, theoretical chemists faced insurmountable mathematical barriers in solving quantum mechanical equations for all but the simplest systems, leaving them unable to make quantitative predictions about molecular behavior [3] [19].

The dawn of digital chemistry emerged from a convergence of factors: the foundational work of theoretical physicists in the 1920s-1940s, the rapid development of digital computer technology during and after World War II, and the pioneering efforts of chemists who recognized the potential of these new tools [19] [20]. This transformation occurred within the broader context of chemistry's historical development, where the exponential growth in chemical discovery had already been established, with new compounds reported at a stable 4.4% annual growth rate from 1800 to 2015 [4] [5].

This article examines the groundbreaking work of the 1950s and 1960s that laid the foundation for modern computational chemistry, focusing on the first semi-empirical and ab initio calculations that transformed theoretical concepts into practical computational tools.

Historical and Scientific Context

The Pre-Computational Landscape (Pre-1950)

The groundwork for computational chemistry was established through pioneering theoretical developments in quantum mechanics throughout the early 20th century. The Heitler-London study of 1927, which applied valence bond theory to the hydrogen molecule, represented one of the first successful theoretical calculations in chemistry [3]. This work demonstrated that quantum mechanics could quantitatively describe chemical bonding, yet the mathematical complexity of solving the Schrödinger equation for systems with more than two electrons prevented widespread application of these methods [3].

Throughout the 1930s and 1940s, influential textbooks by Pauling and Wilson, Eyring, Walter and Kimball, and Coulson served as primary references for chemists, establishing the theoretical framework that would later become computationally accessible [3]. During this period, chemistry continued its steady exploration of chemical space, with the proto-organic regime (pre-1860) giving way to the organic regime (1861-1980), characterized by more regular year-to-year output of new compounds dominated by carbon- and hydrogen-containing molecules [4].

The development of electronic computers during World War II provided the essential technological breakthrough that would enable theoretical chemistry to evolve into computational chemistry. In the postwar period, these machines became available for general scientific use, coinciding with a declining interest among physicists in molecular structure problems [19]. This created an opportunity for chemists to establish a new discipline focused on obtaining quantitative molecular information through numerical approximations [19].

The Theoretical Framework

The fundamental challenge that computational chemistry addressed was the many-body problem inherent in quantum mechanical descriptions of chemical systems. The Schrödinger equation, while providing a complete description of a quantum system, was mathematically intractable for systems with more than two electrons without introducing approximations [3] [19].

The time-independent Schrödinger equation for a system of particles is:

[ Hψ = Eψ ]

Where H is the Hamiltonian operator, ψ is the wavefunction, and E is the energy of the system [19]. For molecular systems, the Hamiltonian includes terms for electron kinetic energy, nuclear kinetic energy, and all Coulombic interactions between electrons and nuclei [19].

Two fundamental approaches emerged to make these calculations feasible:

• Ab initio methods: Solving the Schrödinger equation using only fundamental physical constants without empirical parameters [3]
• Semi-empirical methods: Introducing approximations and experimental parameters to simplify calculations [3]

The complexity of these calculations required the computational power that only digital computers could provide, setting the stage for the revolutionary developments of the 1950s.

Foundational Computational Methods

Ab Initio Quantum Chemistry

The term "ab initio" (Latin for "from the beginning") refers to quantum chemical methods that solve the molecular Schrödinger equation using only fundamental physical constants without inclusion of empirical or semi-empirical parameters [3]. These methods are rigorously defined on first principles and aim for solutions within qualitatively known error margins [3].

Ab initio methods require the definition of two essential components:

• Level of theory: The specific mathematical approximations used to solve the Schrödinger equation [3]
• Basis set: A set of functions centered on the molecule's atoms used to describe molecular orbitals via the linear combination of atomic orbitals (LCAO) approach [3]

The Hartree-Fock (HF) method emerged as a common type of ab initio electronic structure calculation, extending molecular orbital theory by including the average effect of electron-electron repulsions but not their specific interactions [3]. As basis set size increases, the energy and wave function tend toward a limit called the Hartree-Fock limit [3]. Going beyond Hartree-Fock requires methods that correct for electron-electron repulsion (electronic correlation), leading to the development of post-Hartree-Fock methods [3].

Semi-Empirical Methods

Semi-empirical methods represent a practical alternative to ab initio calculations by introducing approximations and experimental parameters to simplify computations. These methods reduce computational complexity by neglecting certain integrals or parameterizing them based on experimental data [3].

The development of semi-empirical methods followed a historical progression:

• Hückel method (1964): Used a simple linear combination of atomic orbitals (LCAO) to determine electron energies of molecular orbitals of π electrons in conjugated hydrocarbon systems [3]
• CNDO (1960s): Complete Neglect of Differential Overlap replaced earlier empirical methods with more sophisticated semi-empirical approaches [3]

These methods played a crucial role in extending computational chemistry to larger molecules during the 1960s when computational resources were still limited.

Key Developments and Pioneers (1950-1960)

Major Theoretical and Computational Advances

Table 1: Key Developments in Computational Chemistry (1950-1960)

Year	Development	Key Researchers	Significance
1950-1955	Early polyatomic calculations using Gaussian orbitals	Boys and coworkers [3]	First configuration interaction calculations performed on EDSAC computer
1951	LCAO MO approach paper	Clemens C. J. Roothaan [3]	Established foundational methodology; became second-most cited paper in Reviews of Modern Physics
1956	First ab initio Hartree-Fock calculations on diatomic molecules	MIT researchers [3]	Used basis set of Slater orbitals; demonstrated feasibility of ab initio methods
1960	Systematic study of diatomic molecules with minimum basis set	Ransil [3]	Extended ab initio methods to broader range of systems
1960	First calculation with larger basis set	Nesbet [3]	Demonstrated importance of basis set size for accuracy
1964	Hückel method calculations of conjugated hydrocarbons	Berkeley and Oxford researchers [3]	Applied semi-empirical methods to molecules ranging from butadiene to ovalene

The 1950s witnessed foundational work that established the core methodologies of computational quantum chemistry. Although this decade produced virtually no predictions of chemical interest, it established the essential framework for future applications [21]. Much of this fundamental research was conducted in the laboratories of Frank Boys in Cambridge and Clemens Roothaan and Robert Mulliken in Chicago [21].

Significant contributions during this period came from numerous theoretical chemists including Klaus Ruedenberg, Robert Parr, John Pople, Robert Nesbet, Harrison Shull, Per-Olov Löwdin, Isaiah Shavitt, Albert Matsen, Douglas McLean, and Bernard Ransil [21]. Their collective work established the algorithms and mathematical formalisms that would enable practical computational chemistry in the following decades.

Pioneers of Computational Chemistry

Table 2: Key Pioneers in Early Computational Chemistry

Researcher	Institution	Contributions
Frank Boys	Cambridge University	Pioneered use of Gaussian orbitals for polyatomic calculations; performed first configuration interaction calculations [3] [21]
Clemens C. J. Roothaan	University of Chicago	Developed LCAO MO approach; published highly influential 1951 paper that became a foundational reference [3] [21]
Robert Mulliken	University of Chicago	Contributed to molecular orbital theory; provided theoretical foundation for computational approaches [21] [20]
John Pople	Cambridge University	Developed computational methods in quantum chemistry; later awarded Nobel Prize in 1998 [3]
Bernard Ransil		Conducted systematic study of diatomic molecules using minimum basis set (1960) [3]
Robert Nesbet		Performed first calculations with larger basis sets (1960) [3]

The collaborative nature of this emerging field is evident in the network of researchers who built upon each other's work. The cross-pollination of ideas between different research groups accelerated methodological developments, while the sharing of computer programs established a culture of collaboration that would characterize computational chemistry for decades to come.

Experimental Protocols and Methodologies

Early Ab Initio Workflow

The first ab initio calculations followed a systematic workflow that combined theoretical framework with practical computational implementation. The following diagram illustrates the generalized protocol for these pioneering calculations:

The computational process began with the definition of the molecular system, typically focusing on diatomic molecules or small polyatomic systems due to computational constraints [3]. Researchers would then select an appropriate theoretical method, with the Hartree-Fock approach being the most common for early ab initio work [3].

The choice of basis set was critical, with early calculations employing either:

• Slater-type orbitals (STOs): More accurate representation of atomic orbitals but computationally demanding [3]
• Gaussian-type orbitals (GTOs): Computational advantages for integral evaluation, though requiring more functions for equivalent accuracy [3]

The input preparation involved specifying molecular coordinates and basis set definitions, followed by the computation of one- and two-electron integrals and the self-consistent field (SCF) procedure to solve the Hartree-Fock equations iteratively [3].

Technical Specifications of Early Calculations

The first ab initio calculations were characterized by severe limitations in both hardware and methodology:

• Basis sets: Early calculations used minimal basis sets with just enough functions to accommodate the electrons of the constituent atoms [3]
• Integral evaluation: Computation of two-electron integrals presented significant computational challenges, with early calculations often neglecting or approximating certain classes of integrals [3]
• SCF convergence: The self-consistent field procedure required iterative solution, with convergence often problematic for early calculations [3]
• Computer systems: Calculations were performed on mainframe computers such as EDSAC with limited memory and processing speed by modern standards [3]

Despite these limitations, these pioneering calculations established the protocols and methodologies that would be refined throughout the following decades.

Research Reagent Solutions

Table 3: Essential Computational "Reagents" in Early Quantum Chemistry

Resource	Type	Function	Examples
Basis Sets	Mathematical Functions	Describe atomic and molecular orbitals	Slater-type orbitals (STOs), Gaussian-type orbitals (GTOs) [3]
Theoretical Methods	Computational Algorithms	Approximate solution to Schrödinger equation	Hartree-Fock, Configuration Interaction, Valence Bond [3]
Computer Programs	Software	Implement computational methods	ATMOL, Gaussian, IBMOL, POLYAYTOM [3]
Integral Packages	Mathematical Routines	Compute one- and two-electron integrals	Fundamental for molecular orbital calculations [3]
SCF Algorithms	Numerical Methods	Solve self-consistent field equations	Iterative procedures for Hartree-Fock calculations [3]

The "research reagents" of computational chemistry differed fundamentally from those of experimental chemistry, consisting of mathematical tools and computational resources rather than chemical substances. The basis set served as the fundamental building block, with Slater-type orbitals used in the first diatomic calculations and Gaussian-type orbitals enabling the first polyatomic calculations [3].

Theoretical methods formed the core algorithms that approximated solutions to the Schrödinger equation, with the Hartree-Fock method providing the starting point for most early ab initio work [3]. The development of computer programs such as ATMOL, Gaussian, IBMOL, and POLYAYTOM in the early 1970s represented the culmination of the methodological work begun in the 1950s, though only Gaussian remains in widespread use today [3].

Computational Hardware Environment

The hardware environment for these early calculations presented significant constraints:

• Computer systems: Mainframe computers with limited memory and processing speed compared to modern standards [3]
• Storage: Punch cards and magnetic tape for program input and data storage [3]
• Processing time: Calculations that now take seconds could require days or weeks of computation time [3]
• Programming: Low-level programming languages and manual optimization of computational routines [3]

Despite these limitations, the increasing accessibility of computers throughout the 1950s and 1960s enabled theoretical chemists to perform calculations that were previously impossible [3] [19].

Impact and Historical Significance

Immediate Scientific Impact

The development of computational chemistry in the 1950s and 1960s created a new paradigm for chemical research, establishing a third pillar of chemical investigation alongside experimental and theoretical approaches. While the immediate chemical predictions from early ab initio work were limited, the field laid an essential foundation for future applications [21].

The relationship between computational and theoretical chemistry became clearly defined during this period: theoretical chemists developed algorithms and computer programs, while computational chemists applied these tools to specific chemical questions [3]. This division of labor accelerated progress in both domains, with computational applications highlighting limitations in existing theories and driving methodological improvements.

By the late 1960s, computational chemistry began to achieve notable successes, such as the work by Kolos and Wolniewicz on the hydrogen molecule. Their highly accurate calculations of the dissociation energy diverged from accepted experimental values, prompting experimentalists to reexamine their measurements and ultimately confirming the theoretical predictions [19]. This reversal of the traditional validation process demonstrated the growing maturity and reliability of computational approaches.

Integration into Broader Chemical Research

The emergence of computational chemistry occurred within the broader context of chemical research, which had maintained a stable exponential growth in the discovery of new compounds since 1800 [4] [5]. Computational methods would eventually enhance this exploration of chemical space, though their significant impact on chemical discovery would not be realized until later decades.

The methodologies developed during the 1950s and 1960s established the foundation for computational chemistry's eventual applications in diverse areas including:

• Catalysis research: Analyzing catalytic systems without experiments by calculating energies, activation barriers, and thermodynamic properties [3]
• Drug development: Modeling potentially useful drug molecules to save time and cost in the discovery process [3]
• Materials science: Predicting structures and properties of molecules and solids [3]
• Chemical databases: Storing and searching data on chemical entities [3]

The pioneering work of this era would eventually be recognized through Nobel Prizes in Chemistry awarded to Walter Kohn and John Pople in 1998 and to Martin Karplus, Michael Levitt, and Arieh Warshel in 2013 [3].

The period from 1950 to 1960 represents the true dawn of digital chemistry, when theoretical concepts transformed into practical computational methodologies. The pioneering work in semi-empirical and ab initio calculations established the foundational principles, algorithms, and computational approaches that would enable the explosive growth of computational chemistry in subsequent decades.

The development of these early computational methods occurred within the broader historical context of chemistry's steady expansion, characterized by exponential growth in chemical discovery since 1800 [4] [5]. The computational approaches established in the 1950s and 1960s would eventually enhance this exploration of chemical space, though their significant impact would not be fully realized until later decades when computational power increased and methodologies matured.

The collaboration between theoretical chemists, who developed algorithms, and computational chemists, who applied these tools to chemical problems, created a synergistic relationship that accelerated progress in both domains [3]. The methodological framework established during this formative period—encompassing basis sets, theoretical methods, computational algorithms, and validation procedures—continues to underpin modern computational chemistry, demonstrating the enduring legacy of these pioneering efforts.

The evolution of computational chemistry from a theoretical concept to a practical scientific tool represents one of the most significant transformations in modern chemical research. This progression was enabled by fundamental algorithmic breakthroughs in three interdependent areas: the development of the Hartree-Fock method for approximating electron behavior, the creation of basis sets for mathematically representing atomic orbitals, and continuous improvements in computational feasibility through both hardware and software innovations. These developments did not occur in isolation but rather through a complex interplay between theoretical chemistry, physics, mathematics, and computer science.

The trajectory of computational quantum chemistry reveals a fascinating history of interdisciplinary exchange. As noted by historians, quantum chemistry originally occupied an uneasy position "in-between" physics and chemistry before eventually establishing itself as a distinct subdiscipline [22]. This transition was catalyzed by the advent of digital computers, which enabled the practical application of theoretical frameworks that had been developed decades earlier. The period around 1990 marked a particularly significant turning point, often described as the "computational turn" in quantum chemistry, characterized by new modeling conceptions, decentralized computing infrastructure, and market-like organization of the field [22].

This review examines the intertwined development of Hartree-Fock methodologies, basis set formulations, and the progressive enhancement of computational feasibility that together transformed quantum chemistry from a theoretical endeavor to an indispensable tool across chemical disciplines.

Historical Foundations: From Theoretical Concepts to Practical Computation

The Pre-Computing Era (1920s-1950s)

The foundational work in quantum chemistry began long before digital computers became available. The Hartree-Fock method was developed through contributions by Douglas Rayner Hartree in 1928 and Vladimir Fock in 1930 [23]. Hartree's original self-consistent field (SCF) method neglected quantum exchange effects, while Fock's extension incorporated these critical phenomena through the use of Slater determinants, creating what we now recognize as the full Hartree-Fock method [23].

Table: Key Historical Developments in Early Quantum Chemistry (1920s-1950s)

Year	Developer	Contribution	Significance
1928	Douglas Hartree	Self-consistent field method	First practical approximation for many-electron systems
1930	Vladimir Fock	Incorporation of exchange	Added quantum exchange effects via Slater determinants
1929	John Slater	Slater-type orbitals	Physically motivated orbital representations
1950s	Frank Boys	Gaussian-type orbitals	Computationally efficient orbital representations

During this period, computational limitations significantly constrained application of these methods. Calculations were performed using mechanical desktop calculators, and even simple atoms required tremendous effort [23]. For instance, Hartree's calculations for helium and various ions demonstrated the method's potential but also highlighted its computational intensiveness [23]. The 1930s-1950s were far from years of stagnation, however, as important conceptual and mathematical clarifications occurred, particularly regarding the physical interpretation of quantum exchange phenomena [23].

The Early Computing Revolution (1950s-1970s)

The development of digital computers in the post-war period dramatically altered the landscape of quantum chemistry. A pivotal moment came in 1951 with the Shelter Island conference on quantum-mechanical methods, where researchers recognized both the potential and challenges of computational approaches [22]. The transition from mechanical calculators to electronic computers reduced calculation times from weeks to hours or minutes, enabling applications to increasingly complex molecular systems [23].

Frank Boys' crucial insight that Slater-type orbitals (STOs) could be approximated as linear combinations of Gaussian-type orbitals (GTOs) represented a breakthrough in computational efficiency [24]. While STOs provide more physically accurate representations, particularly near atomic nuclei, the product of two GTOs can be written as a linear combination of other GTOs, enabling enormous computational savings by simplifying integral calculations [24]. This innovation made practical quantum chemistry calculations feasible and was instrumental to the field's growth.

The Hartree-Fock Method: Foundation of Ab Initio Quantum Chemistry

Theoretical Framework

The Hartree-Fock method operates within the Born-Oppenheimer approximation, which separates nuclear and electronic motions due to their significant mass difference. The electronic Schrödinger equation is then solved for a fixed nuclear configuration. The fundamental approximation in Hartree-Fock theory is that each electron moves independently in an average field created by all other electrons and the nuclei.

The Hartree-Fock wavefunction is constructed as a Slater determinant of molecular orbitals, which ensures that the wavefunction obeys the Pauli exclusion principle through its antisymmetry with respect to electron exchange [23]. This antisymmetry naturally incorporates quantum exchange effects, which are purely quantum mechanical phenomena with no classical analogue. The method determines the optimal molecular orbitals by solving the Hartree-Fock equations:

[ \hat{f}(\mathbf{r}i) \psii(\mathbf{r}i) = \epsiloni \psii(\mathbf{r}i) ]

where (\hat{f}) is the Fock operator, (\psii) are the molecular orbitals, and (\epsiloni) are the orbital energies. These equations must be solved self-consistently because the Fock operator itself depends on the molecular orbitals.

Diagram Title: Hartree-Fock Self-Consistent Field (SCF) Procedure

Limitations and the Electron Correlation Problem

While Hartree-Fock provides a qualitatively correct description of molecular electronic structure, it suffers from a fundamental limitation: it neglects electron correlation, meaning it does not account for the correlated motion of electrons [25]. The Hartree-Fock method treats electrons as moving independently in an average field, but in reality, electrons avoid each other due to Coulomb repulsion. This correlation error typically amounts to ~1% of the total energy, but this small percentage can represent significant energy quantities in chemical terms—often enough to render quantitative predictions inaccurate [25].

The recognition of this limitation led to the development of post-Hartree-Fock methods, including:

• Møller-Plesset Perturbation Theory: Adds electron correlation through Rayleigh-Schrödinger perturbation theory [25]
• Configuration Interaction: Generates a wavefunction as a linear combination of Slater determinants with different electron configurations [26]
• Coupled Cluster Theory: Uses an exponential ansatz to incorporate electron correlation effects, often considered the "gold standard" for single-reference calculations [27]

These post-Hartree-Fock methods systematically improve upon Hartree-Fock results but at significantly increased computational cost, creating an enduring tension between accuracy and feasibility in quantum chemical calculations.

Basis Sets: Mathematical Representation of Atomic Orbitals

Basis Set Fundamentals and Types

In computational quantum chemistry, a basis set is a set of mathematical functions (called basis functions) used to represent electronic wavefunctions [24]. The use of basis sets converts the partial differential equations of quantum mechanical models into algebraic equations suitable for computer implementation [24]. Conceptually, this is equivalent to an approximate resolution of the identity, where molecular orbitals (|ψ_i⟩) are expanded as linear combinations of basis functions (|μ⟩):

[ |ψi⟩ ≈ ∑μ c_{μi} |μ⟩ ]

where (c_{μi}) are the expansion coefficients determined by solving the Hartree-Fock equations [24].

Table: Common Types of Basis Sets in Quantum Chemistry

Basis Set Type	Description	Advantages	Limitations
Minimal Basis Sets (e.g., STO-3G)	One basis function per atomic orbital	Computational efficiency; good for large systems	Low accuracy; insufficient for research publications
Split-Valence Basis Sets (e.g., 6-31G)	Multiple functions for valence orbitals	Improved description of chemical bonding	Increased computational cost
Polarized Basis Sets (e.g., 6-31G*)	Addition of functions with higher angular momentum	Describe deformation of electron density	Further increased computational requirements
Diffuse Functions (e.g., 6-31+G)	Addition of widely-spread functions	Better description of anions, weak interactions	Significant increase in basis set size
Correlation-Consistent (e.g., cc-pVNZ)	Systematic construction for correlated methods	Designed to approach complete basis set limit	High computational cost for large N

The Pople Notation System

The notation system developed by John Pople's group provides a concise description of basis set composition [24]. In an X-YZg basis set:

• X indicates the number of primitive Gaussian functions comprising each core atomic orbital basis function
• Y and Z indicate that valence orbitals are composed of two basis functions each, composed of linear combinations of Y and Z primitive Gaussian functions, respectively [24]

Additional notations specify enhancements:

• * (asterisk) indicates polarization functions on heavy atoms
• (double asterisk) indicates polarization functions on all atoms including hydrogen
• + (plus) indicates diffuse functions on heavy atoms
• ++ (double plus) indicates diffuse functions on all atoms [24]

For example, the 6-311+G basis set uses 6 primitive Gaussians for core orbitals, triple-zeta quality for valence orbitals (composed of 3, 1, and 1 primitive Gaussians), with diffuse functions on heavy atoms.

Basis Set Convergence and Completeness

The concept of the complete basis set (CBS) limit is fundamental to understanding basis set development [24]. As the number of basis functions increases toward an infinite complete set, calculations approach this limit, representing the exact solution within the constraints of the method (Hartree-Fock, DFT, etc.) [24]. In practice, computational constraints prevent reaching the true CBS limit, necessitating careful selection of appropriate basis sets.

Different basis set families are optimized for specific computational methodologies. While Pople-style basis sets are efficient for Hartree-Fock and DFT calculations [24], correlation-consistent basis sets (developed by Dunning and coworkers) are specifically designed for systematic convergence to the CBS limit in post-Hartree-Fock calculations [24]. These are denoted as cc-pVNZ, where N = D (double), T (triple), Q (quadruple), 5, 6, etc., indicating the level of completeness [24].

Diagram Title: Basis Set Hierarchy Toward Completeness

The Path to Computational Feasibility

Algorithmic and Hardware Advances

The transformation of quantum chemistry from a theoretical discipline to a practical tool required addressing profound computational challenges. The combinatorial complexity of quantum mechanical calculations arises from the need to compute numerous electron repulsion integrals, with the formal scaling of naive Hartree-Fock implementations being O(N⁴), where N is the number of basis functions [26].

Key developments that enhanced computational feasibility include:

• Efficient integral evaluation algorithms: Techniques for eliminating negligible integrals and efficient recurrence relations
• Linear algebra optimizations: Improved matrix diagonalization methods essential for solving the Hartree-Fock equations
• Resolution of the Identity (RI) methods: Approximation techniques that reduce computational burden in post-Hartree-Fock methods [28]
• Parallel computing: Distribution of computational workloads across multiple processors

The hardware evolution has been equally significant, transitioning from centralized mainframe architecture to desktop workstations and now to high-performance computing clusters [22]. This democratization of computing power has made quantum chemical calculations accessible to a much broader research community.

The Rise of Density Functional Theory

While not strictly a Hartree-Fock method, Density Functional Theory (DFT) emerged as a pivotal development that dramatically enhanced computational feasibility for many chemical applications [22]. DFT fundamentally differs from wavefunction-based methods by using electron density as the basic variable rather than the many-electron wavefunction [25]. This reformulation reduces the computational complexity while maintaining reasonable accuracy for many chemical applications.

DFT's popularity stems from its favorable accuracy-to-cost ratio, typically scaling as O(N³) compared to O(N⁴) or worse for correlated wavefunction methods [29]. The "combinatorial character" of DFT, with numerous exchange-correlation functionals available for different chemical applications, has contributed to its success and widespread adoption [22]. By the 1990s, DFT had become the dominant method in computational chemistry, particularly for larger molecules and materials simulation [22] [30].

Software Standardization and Commercialization

The development of standardized, user-friendly software packages has been instrumental in making computational quantum chemistry accessible to non-specialists. Packages such as Gaussian, Q-Chem, and MOLPRO provide implemented methods that researchers can apply without programming their own solutions [26]. This commercialization and standardization, particularly Gaussian's transition to a commercial entity in the late 1980s, created a "market-like" organization for computational quantum chemistry [22].

This accessibility came with tradeoffs, however. As noted by researchers, users can perform calculations without understanding the underlying principles, potentially leading to misinterpretation of results [26]. This tension between accessibility and understanding remains an ongoing consideration in the field.

Table: Key Computational Resources and Their Functions

Resource Category	Specific Examples	Function/Purpose
Software Packages	Gaussian, Q-Chem, MOLPRO, CFOUR	Implement quantum chemical methods for practical applications
Basis Set Libraries	Basis Set Exchange, EMSL	Provide standardized basis sets for different elements and accuracy levels
Density Functionals	B3LYP, PBE, M06-2X, ωB97X-D	Approximate exchange-correlation effects in DFT calculations
Solvation Models	PCM (Polarizable Continuum Model), SMD (Solvation Model based on Density)	Account for solvent effects in calculations
Dispersion Corrections	Grimme's D3, D4	Add van der Waals interactions typically missing in standard DFT
Wavefunction Methods	MP2, CCSD(T), CASSCF	Provide higher accuracy through electron correlation treatment

Methodological Protocols: Performing a Quantum Chemical Calculation

Standard Computational Workflow

A typical quantum chemical investigation follows a systematic workflow:

• System Preparation

  • Construct molecular geometry using chemical intuition or experimental data
  • Ensure appropriate initial geometry to facilitate convergence

• Method Selection

  • Choose computational method based on system size and accuracy requirements
  • Select appropriate basis set considering computational cost and target accuracy
  • For DFT calculations, choose exchange-correlation functional based on benchmarking studies [29]

• Geometry Optimization

  • Optimize molecular structure to locate minima on potential energy surface
  • Verify convergence through examination of energy changes and gradients

• Frequency Calculation

  • Compute vibrational frequencies to confirm stationary point character (minimum vs. transition state)
  • Obtain thermodynamic corrections for energy calculations

• Property Evaluation

  • Calculate desired molecular properties (energies, spectra, molecular orbitals, etc.)
  • Perform analysis using appropriate tools (NBO, AIM, etc.)

Assessment of the Potential Energy Surface

The concept of the Potential Energy Surface (PES) is fundamental to computational chemistry [25]. The PES represents the energy of a molecular system as a function of nuclear coordinates. Critical points on the PES include:

• Minima: Correspond to stable molecular structures (reactants, products, intermediates)
• Transition states: First-order saddle points connecting minima along reaction pathways
• Higher-order saddle points: Less chemically relevant stationary points

Exploring the PES allows researchers to understand reaction mechanisms and kinetics by locating these critical points and computing the energy barriers between them [25]. Modern computational chemistry investigations typically compute geometries and energies of starting materials, intermediates, products, and transition states to construct comprehensive reaction profiles [25].

The development of computational quantum chemistry represents a remarkable convergence of theoretical insight, mathematical innovation, and technological advancement. The intertwined evolution of Hartree-Fock methodologies, basis set formulations, and computational infrastructure has transformed quantum chemistry from a theoretical specialty to an essential tool across chemical disciplines.

This transformation has occurred through successive waves of innovation: the initial theoretical developments in the pre-computer era, the algorithmic breakthroughs that enabled practical computation, the hardware advances that democratized access, and most recently, the emergence of artificial intelligence methods that promise to further revolutionize the field [27]. Throughout this history, the fundamental tension between computational feasibility and physical accuracy has driven innovation, with researchers continually developing new methods to push the boundaries of what is computationally possible while maintaining physical meaningfulness.

The future of computational quantum chemistry appears likely to be shaped by emerging artificial intelligence approaches, such as the AIQM1 method, which leverages machine learning to improve upon semi-empirical quantum mechanical methods, achieving accuracy comparable to coupled-cluster theory at dramatically reduced computational cost [27]. These AI-enhanced methods represent a new paradigm in which computational feasibility is no longer solely dependent on algorithmic scaling or hardware improvements but also on data-driven approaches that learn from high-accuracy reference calculations.

As computational quantum chemistry continues to evolve, the historical interplay between methodological development and computational feasibility ensures that researchers will continue to push the boundaries of system size, accuracy, and physical insight, further solidifying the field's role as an indispensable component of modern chemical research.

The evolution of computational chemistry from the 19th century to the present represents a fundamental transformation in how scientists investigate molecular matter. This field has matured from theoretical foundations to practical methodologies that complement traditional experimental approaches. Central to this narrative is the development of molecular mechanics (MM) and sophisticated software packages like Gaussian, which have empowered researchers to explore chemical space with unprecedented precision. Molecular mechanics, characterized by its application of classical physics to molecular systems, provides the foundational framework for understanding molecular conformations and interactions through force fields. The MM2 force field, developed by Norman Allinger, and its successors set new standards for accuracy in calculating molecular structures and energies for organic molecules. Concurrently, the Gaussian software platform, initiated by John Pople, revolutionized quantum mechanical calculations, eventually incorporating molecular mechanics methods to create powerful multi-layered approaches. This whitepaper examines the technical foundations, historical development, and practical applications of these transformative tools within the broader context of computational chemistry's expansion from 1800 to 2015, focusing specifically on their critical roles in modern scientific research and drug development.

Table: Major Historical Regimes in Chemical Exploration (1800-2015)

Regime	Period	Annual Growth Rate (%)	Key Characteristics
Proto-organic	Before 1861	4.04	High variability in compound reporting; dominated by extraction and analysis of natural products
Organic	1861-1980	4.57	Guided production driven by structural theory; established synthesis as primary discovery tool
Organometallic	1981-2015	2.96 (overall)	Decreased variability; emergence of organometallic compounds as dominant focus

Data derived from Reaxys database analysis of over 14 million compounds [4]

Historical Backdrop: The Evolution of Chemical Discovery

The trajectory of chemical discovery from 1800 to 2015 reveals distinct phases of exponential growth in reported compounds, unaffected even by major world events. Analysis of the Reaxys database, containing millions of chemical reactions and compounds, demonstrates that the annual number of new compounds grew exponentially at a stable 4.4% annual rate throughout this 215-year period [4]. This growth pattern persisted through World Wars and scientific paradigm shifts, indicating the relentless expansion of chemical exploration.

The period before 1861, termed the "proto-organic" regime, was characterized by uncertain year-to-year output of both organic and inorganic compounds. During this era, chemical exploration primarily occurred through extraction and analysis of animal and plant products, though synthesis played a more substantial role than traditionally acknowledged. The period from 1861 to 1980, designated the "organic" regime, witnessed more regular and guided production of compounds following the establishment of structural theory. This century-long phase cemented synthesis as the established methodology for reporting new compounds. The current "organometallic" regime, beginning around 1981, represents the most regular period of chemical production, with organometallic compounds emerging as a dominant focus [4].

Throughout these regimes, analysis of starting materials in synthesis reveals remarkable conservation in chemist preferences. Despite the growing production of new compounds, most belong to a restricted set of chemical compositions, suggesting constrained exploration pathways within the broader chemical space [4]. This historical context sets the stage for understanding how computational methods emerged as essential tools for navigating and expanding this rapidly growing chemical universe.

The Rise of Molecular Mechanics and Force Fields

Theoretical Foundations

Molecular mechanics operates on the principle that molecular systems can be accurately modeled using classical mechanics, treating atoms as spheres and bonds as springs. This approach relies on the Born-Oppenheimer approximation, which assumes that the potential energy of a system can be calculated as a function of nuclear coordinates using force fields [31]. The fundamental functional form of a molecular mechanics force field partitions the total potential energy into bonded and non-bonded components:

E_total = E_bonded + E_nonbonded [32]

Where the bonded terms are further decomposed as:

E_bonded = E_bond + E_angle + E_dihedral [32]

And the non-bonded terms include:

E_nonbonded = E_electrostatic + E_van der Waals [32]

This conceptual framework provides the mathematical basis for calculating molecular potential energy surfaces without explicitly treating electrons, dramatically reducing computational cost compared to quantum mechanical methods.

Force Field Components and Parameterization

The accuracy of molecular mechanics simulations depends critically on the specific functional forms and parameters that constitute a force field. Bond stretching is typically modeled using a harmonic potential: E_bond = k_ij/2(l_ij - l_0,ij)², where k_ij represents the bond force constant, l_ij the actual bond length, and l_0,ij the equilibrium bond length [32]. For more accurate reproduction of vibrational spectra, the Morse potential can be employed instead at greater computational expense. Angle bending terms similarly employ harmonic potentials around equilibrium bond angles.

Dihedral or torsional terms present greater complexity due to multiple minima and are typically modeled using cosine functions: ∑∑K_ϕ,n(1 + cos(nϕ - δ_n)), where n represents multiplicity, K_ϕ,n the force constant, and δ_n the phase angle [33]. Non-bonded interactions comprise van der Waals forces, typically modeled with Lennard-Jones 6-12 potentials, and electrostatic interactions described by Coulomb's law between fixed partial atomic charges [32] [33].

Force field parameterization represents a significant challenge, with parameters derived from experimental data, quantum mechanical calculations, or both. The parametrization strategy can be "component-specific" for individual substances or "transferable" with parameters designed as building blocks applicable to different substances [32]. Force fields are generally categorized as all-atom (explicitly representing every atom), united-atom (treating hydrogen atoms implicitly with their bonded carbon), or coarse-grained (further simplifying groups of atoms into interaction sites) [32].

The MM2 Force Field and Its Progeny

The MM2 force field, developed by Norman Allinger, represented a watershed in molecular mechanics accuracy for organic molecules. Through careful parameterization and inclusion of specific terms like anharmonic potentials and cross-terms, MM2 achieved remarkable precision in predicting molecular structures and properties. For hydrocarbons, the MM4 force field (successor to MM2) calculated heats of formation with an RMS error of 0.35 kcal/mol, vibrational spectra with RMS error of 24 cm⁻¹, rotational barriers with RMS error of 2.2°, C-C bond lengths within 0.004 Å, and C-C-C angles within 1° [31].

This unprecedented accuracy stemmed from Allinger's attention to higher-order terms in the potential energy function. Class II and III force fields incorporate cubic and/or quartic terms in bond and angle potentials: E_bond = K_b(b - b_0)² + K_b'(b - b_0)³ + K_b″(b - b_0)⁴ + ... [33]. Additionally, cross terms representing coupling between internal coordinates (e.g., bond-bond, bond-angle, angle-torsion) significantly improve the reproduction of quantum mechanical potential energy surfaces and experimental properties [33].

Table: Molecular Mechanics Force Field Components

Energy Component	Functional Form	Parameters Required	Physical Basis
Bond Stretching	E_bond = K_b(b - b_0)²	K_b, b_0	Vibrational spectroscopy
Angle Bending	E_angle = K_θ(θ - θ_0)²	K_θ, θ_0	Molecular vibrations
Dihedral/Torsion	E_dihedral = ∑K_ϕ,n(1 + cos(nϕ - δ_n))	K_ϕ,n, n, δ_n	Rotational barriers
van der Waals	E_vdW = ε_ij[(R_min,ij/r_ij)¹² - 2(R_min,ij/r_ij)⁶]	ε_ij, R_min,ij	Noble gas properties
Electrostatic	E_elec = (q_iq_j)/(4πDr_ij)	q_i, q_j	Dipole moments

Gaussian: Revolutionizing Computational Chemistry

Historical Development and Capabilities

The Gaussian computational chemistry package, first released in 1970 as Gaussian 70 by John Pople and his research group at Carnegie Mellon University, fundamentally transformed the practice of computational chemistry [34]. The software was named for Pople's use of Gaussian-type orbitals rather than Slater-type orbitals to speed up molecular electronic structure calculations—a strategic choice to enhance performance on the limited computing hardware of the era [34]. Originally distributed through the Quantum Chemistry Program Exchange, Gaussian has been continuously developed and updated since its initial release, with Gaussian 16 representing the current version as of 2017 [34].

Gaussian's development history reflects the evolution of computational chemistry methodology: Gaussian 70, Gaussian 76, Gaussian 80, Gaussian 82, Gaussian 86, Gaussian 88, Gaussian 90, Gaussian 92, Gaussian 92/DFT, Gaussian 94, Gaussian 98, Gaussian 03, Gaussian 09, and Gaussian 16 [34]. This progression illustrates the continuous incorporation of new theoretical methods and algorithmic improvements. Since 1987, Gaussian has been developed and licensed by Gaussian, Inc., following initial licensing through Carnegie Mellon University [34].

Methodological Spectrum

Gaussian provides a comprehensive suite of computational methods spanning multiple theoretical frameworks. According to the Gaussian manual, the software package encompasses molecular mechanics (AMBER, UFF, DREIDING force fields), semi-empirical quantum chemistry methods, self-consistent field (SCF) methods, Møller–Plesset perturbation theory (MP2, MP3, MP4, MP5), density functional theory (DFT) with various functionals including B3LYP, PBE, and others, ONIOM multi-layer integrated methods, complete active space (CAS) and multi-configurational self-consistent field calculations, coupled cluster methods, quadratic configuration interaction (QCI) methods, and composite methods such as CBS-QB3, G1, G2, and G3 for high-accuracy energy calculations [34].

The integration of molecular mechanics methods within Gaussian specifically supports three force fields: Amber, Dreiding, and UFF [35]. These implementations were originally developed for use in ONIOM calculations but are also available as independent methods. Gaussian provides significant flexibility in force field customization, allowing users to modify parameters through "soft" parameters specified in the input stream, with various precedence options controlling how these interact with built-in "hard-wired" parameters [35].

Integration of Methods: Multi-Layered Approaches

The ONIOM Framework

A significant advancement in computational methodology emerged with the development of multi-layered approaches, particularly the ONIOM (Our own N-layered Integrated molecular Orbital and molecular Mechanics) method implemented in Gaussian. This framework enables different regions of a molecular system to be treated with different levels of theory, combining the accuracy of quantum mechanical methods with the computational efficiency of molecular mechanics [34]. ONIOM can accommodate up to three layers, typically with higher-level theories (e.g., DFT) applied to chemically active regions and molecular mechanics describing the surrounding environment [34].

The ONIOM method employs a subtractive scheme for energy calculation: E_ONIOM = E_high,model + E_low,real - E_low,model, where "high" and "low" refer to different levels of theory, and "real" and "model" designate different parts of the molecular system [36]. This approach allows for accurate treatment of localized phenomena such as bond breaking and formation while maintaining computational feasibility for large systems.

QM/MM Methodology

The broader QM/MM (Quantum Mechanics/Molecular Mechanics) approach, pioneered by Warshel and Levitt in 1976, has become the most popular method for studying enzymatic reactions [36]. In this methodology, the active site where chemical reactions occur is treated quantum mechanically, while the remainder of the enzyme and solvent environment is modeled using molecular mechanics force fields [36].

The additive QM/MM scheme calculates the total energy as: E_QM/MM^add = E_MM(O) + E_QM(I) + E_QM/MM(I,O), where O represents the outer MM region, I the inner QM region, and E_QM/MM(I,O) describes the coupling between them [36]. This coupling term comprises van der Waals, electrostatic, and bonded contributions, with the electrostatic embedding approach providing the most accurate treatment by incorporating the MM charge environment as a one-electron term in the QM Hamiltonian [36].

Diagram: Integration of Molecular Mechanics and Quantum Mechanics in Multi-layer Computational Approaches

Practical Implementation and Protocols

Molecular Mechanics Specifications in Gaussian

Implementation of molecular mechanics calculations in Gaussian requires careful specification of atom types, which determine the functions and parameters applied within the force field. For a single element such as carbon, multiple MM atom types may exist depending on hybridization and chemical environment [35]. Gaussian automatically assigns atom types for UFF and Dreiding calculations, but Amber calculations require explicit specification within the molecule specification section (e.g., "C-CT" for an SP3 aliphatic carbon atom in the Amber force field) [35].

Partial atomic charges used for electrostatic calculations can be specified explicitly or assigned automatically using the QEq (Charge Equilibration) method developed by Rappe [35]. The syntax for specifying atom types and charges follows the pattern: Element-Type-Charge, with hyphens as separators (e.g., "C-CT-0.32" specifies an SP3 aliphatic carbon with partial charge +0.32) [35].

For molecular dynamics simulations or energy minimization, the connectivity between atoms must be explicitly defined using Geom=Connectivity, especially when bond orders are ambiguous or starting geometries are approximate [35]. Gaussian includes switching function options to manage non-bonded interaction cutoffs, with VRange setting the van der Waals cutoff and CRange setting the Coulomb cutoff distance [35].

Research Reagent Solutions: Computational Tools

Table: Essential Computational Research Reagents in Molecular Modeling

Tool/Reagent	Function	Application Context
AMBER Force Field	Biomolecular molecular mechanics	Protein, nucleic acid simulations
UFF (Universal Force Field)	General-purpose molecular mechanics	Broad applicability across periodic table
DREIDING Force Field	General organic/organometallic molecular mechanics	Drug design, material science
QEq Charge Model	Automatic charge assignment	Electrostatic calculations
ONIOM Framework	Multi-layer integrated calculations	Complex systems requiring multiple theory levels
Lennard-Jones Potential	van der Waals interactions	Non-bonded energy calculations
Coulomb's Law	Electrostatic interactions	Polar molecules, ionic compounds

Applications in Drug Discovery and Materials Science

The integration of molecular mechanics and quantum chemical methods through packages like Gaussian has transformed structure-based drug discovery. Molecular mechanics force fields remain the method of choice for protein simulations, which are essential for studying conformational flexibility—a critical factor in drug binding [33]. Most computational structure-based drug discovery (CSBDD) projects employ molecular mechanics to investigate binding constants, protein folding kinetics, protonation equilibria, active site coordinates, and binding site design [33] [31].

In drug discovery contexts, molecular mechanics enables the calculation of binding free energies through methods such as molecular dynamics simulations and free energy perturbation theory. The ability to simulate proteins in explicit solvent environments with reasonable computational expense makes molecular mechanics indispensable for studying biomolecular recognition and drug-receptor interactions [33]. While quantum mechanical methods provide superior accuracy for electronic properties, their computational demands render them prohibitive for full protein simulations on relevant timescales.

Beyond pharmaceutical applications, these computational methods have found extensive use in materials science, catalysis design, and environmental chemistry. The CATCO research group, for instance, has applied computational methods to design new catalysts, describe hydrogen bonds in proteins, and develop chelating organic molecules for removing toxic metals from wastewater [9]. The versatility of these tools across scientific disciplines underscores their fundamental importance in modern chemical research.

The historical development of computational chemistry from 1800 to 2015 reveals a consistent expansion of chemical exploration, characterized by exponential growth in reported compounds. Within this narrative, the rise of molecular mechanics methods and the Gaussian software platform represents a transformative period where computational approaches became indispensable partners to experimental investigation. The technical sophistication embodied in force fields like MM2 and software environments like Gaussian has enabled researchers to navigate chemical space with unprecedented precision and insight.

The integration of molecular mechanics and quantum mechanics through multi-layered approaches such as ONIOM has created powerful methodologies for addressing complex chemical problems across diverse domains, from drug discovery to materials design. As computational power continues to grow and methodologies further refine, these tools will undoubtedly remain central to chemical research, continuing the legacy of innovation established by pioneers like Pople, Allinger, and their contemporaries. The ongoing development of more accurate force fields, efficient algorithms, and integrated multi-scale methods ensures that computational chemistry will maintain its vital role at the frontier of chemical discovery.

The evolution of computational chemistry from the 19th century to the present represents a paradigm shift in how scientists investigate molecular structure and reactivity. By the late 20th century, this evolution culminated in two transformative advances recognized by the Nobel Committee: Density-Functional Theory (DFT) and Multiscale Modeling. The 1998 Nobel Prize in Chemistry awarded to Walter Kohn and John Pople recognized DFT's revolutionary approach to electronic structure calculation, while the 2013 Prize awarded to Martin Karplus, Michael Levitt, and Arieh Warshel honored multiscale modeling for bridging quantum and classical physics in complex systems [37] [38]. These methodologies provided the foundational framework enabling modern computational investigations across chemistry, materials science, and drug discovery.

This technical guide examines the theoretical foundations, developmental timelines, key methodologies, and practical implementations of these Nobel Prize-winning advances. Designed for researchers, scientists, and drug development professionals, it provides both historical context and technical specifications to facilitate advanced application within contemporary research environments.

Density-Functional Theory (DFT)

Theoretical Foundations and Historical Development

Density-Functional Theory represents a computational quantum mechanical approach that revolutionized the prediction of electronic structure in atoms, molecules, and materials. Unlike wavefunction-based methods that track 3N variables for N electrons, DFT simplifies the problem by focusing on electron density—a function of just three spatial coordinates [39]. This conceptual leap made accurate quantum mechanical calculations feasible for complex systems previously intractable to theoretical treatment.

The theoretical underpinnings of DFT rest on two foundational theorems established by Hohenberg and Kohn in 1964 [40] [39]:

• Theorem 1: All properties of a ground-state quantum mechanical system are uniquely determined by its electron density, ρ(r).
• Theorem 2: A universal functional for the energy E[ρ] exists in terms of the density ρ(r), and the exact ground-state density minimizes this energy functional.

The practical implementation of DFT emerged through the Kohn-Sham equations introduced in 1965, which proposed mapping the real interacting system of electrons onto a fictitious non-interacting system with the same electron density [41] [40]. This approach separated the computationally challenging components of the quantum many-body problem:

[ \left[-\frac{\hbar^2}{2m}\nabla^2 + V{\text{ext}}(\mathbf{r}) + V{\text{H}}(\mathbf{r}) + V{\text{XC}}(\mathbf{r})\right] \psii(\mathbf{r}) = \epsiloni \psii(\mathbf{r}) ]

where (V{\text{ext}}) is the external potential, (V{\text{H}}) is the Hartree potential, and (V_{\text{XC}}) is the exchange-correlation potential that encapsulates all quantum many-body effects [42].

Table 1: Historical Development of Density-Functional Theory

Year	Development	Key Contributors	Significance
1927	Thomas-Fermi Model	Thomas, Fermi	First statistical model to approximate electron distribution using density rather than wavefunction [40]
1964	Hohenberg-Kohn Theorems	Hohenberg, Kohn	Established theoretical foundation proving density alone could determine all system properties [40]
1965	Kohn-Sham Equations	Kohn, Sham	Provided practical computational framework introducing non-interacting reference system [41] [40]
1965	Local Density Approximation (LDA)	Kohn, Sham	First approximation for exchange-correlation functional; accurate for simple metals [40]
1980s	Generalized Gradient Approximations (GGA)	Becke, Perdew, Parr, Yang	Improved accuracy by incorporating density gradient; made DFT useful for chemistry [40]
1993	Hybrid Functionals	Becke	Mixed Hartree-Fock exchange with DFT functionals; significantly improved accuracy [40]
1998	Nobel Prize in Chemistry	Kohn (DFT), Pople (computational methods)	Recognized transformative impact of DFT on quantum chemistry [43] [44] [39]
2001	Jacob's Ladder Classification	Perdew	Categorized functionals in a hierarchy of increasing complexity and accuracy [40]
2020s	Machine Learning Enhancements	Microsoft Research and others	Applied deep learning to develop more accurate functionals beyond traditional constraints [40]

Key Methodologies and Experimental Protocols

The Kohn-Sham Self-Consistent Field Approach

The practical implementation of DFT follows an iterative Self-Consistent Field (SCF) procedure to solve the Kohn-Sham equations [40]. The workflow begins with an initial guess for the electron density, constructs the Kohn-Sham Hamiltonian, solves for the eigenfunctions and eigenvalues, constructs a new density from the occupied orbitals, and iterates until convergence is achieved. The specific steps include:

• Initialization: Generate starting electron density guess, often from superposition of atomic densities
• Hamiltonian Construction: Build Kohn-Sham Hamiltonian with current density
• Wavefunction Solution: Solve Kohn-Sham equations for orbitals ψᵢ and energies εᵢ
• Density Update: Construct new electron density from occupied orbitals: ( \rho(\mathbf{r}) = \sum{i=1}^{N} |\psii(\mathbf{r})|^2 )
• Convergence Check: Compare input and output densities; if not converged, mix densities and return to step 2

This SCF procedure transforms the intractable many-electron problem into a manageable computational routine executable on modern high-performance computing systems.

Exchange-Correlation Functionals

The accuracy of DFT calculations critically depends on the approximation used for the exchange-correlation functional. The evolution of these functionals represents the central narrative of DFT development, categorized by Perdew's "Jacob's Ladder" climbing toward "chemical accuracy" [40]:

• Local Density Approximation (LDA): The simplest functional where the exchange-correlation energy depends only on the local electron density: ( E{\text{XC}}^{\text{LDA}}[\rho] = \int \rho(\mathbf{r}) \varepsilon{\text{XC}}(\rho(\mathbf{r})) d\mathbf{r} ). While computationally efficient, LDA suffers from systematic errors including overbinding and inaccurate molecular dissociation energies [40] [42].

• Generalized Gradient Approximation (GGA): Improves upon LDA by including the density gradient: ( E{\text{XC}}^{\text{GGA}}[\rho] = \int \rho(\mathbf{r}) \varepsilon{\text{XC}}(\rho(\mathbf{r}), \nabla\rho(\mathbf{r})) d\mathbf{r} ). Popular GGA functionals include PBE (Perdew-Burke-Ernzerhof) and BLYP (Becke-Lee-Yang-Parr) [42].

• Meta-GGA Functionals: Further incorporate the kinetic energy density: ( \tau(\mathbf{r}) = \sum{i}^{\text{occ}} |\nabla\psii(\mathbf{r})|^2 ), providing improved accuracy for molecular properties and reaction barriers.

• Hybrid Functionals: Mix a portion of exact Hartree-Fock exchange with DFT exchange-correlation: ( E{\text{XC}}^{\text{hybrid}} = a E{\text{X}}^{\text{HF}} + (1-a) E{\text{X}}^{\text{DFT}} + E{\text{C}}^{\text{DFT}} ). The B3LYP functional remains one of the most widely used hybrids in quantum chemistry [40].

Figure 1: DFT Self-Consistent Field (SCF) Computational Workflow. The iterative procedure for solving Kohn-Sham equations continues until electron density convergence is achieved, typically requiring 10-100 iterations depending on system complexity and initial guess quality.

DFT in Modern Drug Discovery

DFT has emerged as a critical tool in rational drug design, particularly in the investigation of enzyme-inhibitor interactions and reaction mechanisms. During the COVID-19 pandemic, DFT calculations provided crucial insights into SARS-CoV-2 viral proteins and potential inhibitors [42]. Key applications include:

• Reaction Mechanism Elucidation: DFT studies of the SARS-CoV-2 main protease (Mpro) catalytic mechanism revealed the nucleophilic attack process involving the Cys-His catalytic dyad, providing atomic-level understanding of covalent inhibitor action [42].

• Drug-Target Interaction Energy Calculations: DFT computations quantify binding energies between drug candidates and viral targets, enabling virtual screening of compound libraries. For RdRp (RNA-dependent RNA polymerase), DFT has illuminated the incorporation mechanism of nucleotide analogs like remdesivir [42].

• Electronic Property Analysis: DFT calculates frontier molecular orbitals (HOMO-LUMO gaps), electrostatic potentials, and partial atomic charges that influence drug-receptor recognition and binding affinity.

Table 2: DFT Applications in COVID-19 Drug Discovery [42]

SARS-CoV-2 Target	DFT Application	Key Findings	Common Functionals
Main Protease (Mpro)	Reaction mechanism of Cys-His catalytic dyad	Nucleophilic attack mechanism; covalent inhibition pathways	B3LYP, M06-2X, ωB97X-D
RNA-dependent RNA Polymerase (RdRp)	Nucleotide analog incorporation	Transition states and energy barriers for remdesivir incorporation	PBE0, B3LYP-D3
Viral Entry Proteins	Electronic properties of spike protein fragments	Electrostatic potential surfaces for ACE2 recognition	M062X, ωB97X-D
Drug Delivery Systems	Fullerene-based nanocarrier properties	Electronic structure and host-guest interactions	PBE, B3LYP

Multiscale Modeling

Theoretical Foundations and Historical Context

Multiscale modeling addresses the fundamental challenge of simulating biological systems that inherently operate across multiple spatial and temporal scales. As recognized by the 2013 Nobel Prize in Chemistry, the integration of models at different resolutions enables the investigation of complex chemical systems that would be intractable with a single uniform approach [38] [45]. The core insight—that different biological questions require different levels of physical description—has transformed computational biochemistry.

Biological processes span extraordinary ranges of scale: electronic rearrangements during bond formation occur at femtoseconds (10⁻¹⁵ s) and angstroms (10⁻¹⁰ m), while protein folding and molecular assembly processes extend to milliseconds and micrometers [45]. Multiscale modeling provides the conceptual and computational framework to bridge these disparate scales through strategic simplification and focused detail where needed.

The foundational work of Karplus, Levitt, and Warshel established several key principles [37] [45]:

• Hybrid Quantum Mechanics/Molecular Mechanics (QM/MM): Combining quantum mechanical treatment of reactive regions with molecular mechanics description of the environmental surroundings
• Systematic Coarse-Graining: Reducing molecular resolution by representing groups of atoms as single interaction sites
• Hierarchical Integration: Passing information between models at different scales through sequential parameterization

Methodological Approaches and Implementation

QM/MM Methodology

The QM/MM approach partitions the system into two distinct regions [37] [45]:

• QM Region: Treated with quantum mechanical methods (DFT, semiempirical) to model bond breaking/formation, typically encompassing the enzyme active site and substrate
• MM Region: Treated with molecular mechanics force fields to represent protein scaffold and solvent environment

The total energy of the system is calculated as: [ E{\text{total}} = E{\text{QM}} + E{\text{MM}} + E{\text{QM/MM}} ] where (E_{\text{QM/MM}}) describes the interactions between the QM and MM regions, including electrostatic and van der Waals contributions.

Critical implementation considerations include:

• Covalent Boundary Treatment: Handling bonds that cross the QM/MM boundary using link atoms or localized orbitals
• Electrostatic Embedding: Including the MM region partial charges in the QM Hamiltonian to model polarization effects
• Geometry Optimization: Efficiently minimizing energy for both QM and MM degrees of freedom

Sequential and Hybrid Multiscale Schemes

Multiscale modeling implementations generally follow two strategic approaches [45]:

• Sequential (Hierarchical) Scheme: Information from detailed, high-resolution simulations is used to parameterize simplified models for broader application. For example, all-atom molecular dynamics simulations can parameterize coarse-grained models that access longer timescales.

• Hybrid (Concurrent) Scheme: Different regions of the same system are simultaneously modeled at different resolutions, communicating during the simulation. QM/MM represents the classic example, but modern implementations include atomistic/coarse-grained hybrids and continuum/particle hybrids.

Figure 2: Multiscale Modeling Computational Schemes. Sequential approaches parameterize simplified models from detailed simulations, while hybrid approaches simultaneously combine different resolution models with real-time communication.

Applications in Biological Systems

Multiscale modeling has enabled the investigation of complex biological processes that defy single-scale description [45]:

• Enzyme Catalysis: QM/MM approaches reveal the reaction mechanisms of biological catalysts, combining quantum chemical accuracy for bond rearrangements with environmental effects from the protein matrix. Applications span hydrolytic enzymes, oxidoreductases, and transferases.

• Membrane-Protein Interactions: Hybrid models combining atomistic detail for membrane proteins with coarse-grained or continuum descriptions of lipid bilayers enable studies of membrane remodeling, protein insertion, and lipid-protein recognition.

• Cellular Environments: Rigid-body representations of proteins in crowded cellular conditions, informed by atomistic simulations, model the bacterial cytoplasm and its effects on molecular diffusion and association.

Table 3: Multiscale Modeling of Biomolecular Systems [45]

Biological Process	Multiscale Approach	Spatial Scale	Temporal Scale
Enzyme Catalysis	QM/MM	Ångströms to nanometers	Femtoseconds to microseconds
Ion Channel Conductance	Atomistic/Continuum	Nanometers to micrometers	Picoseconds to milliseconds
Protein Folding	Atomistic/Coarse-grained	Nanometers	Nanoseconds to seconds
Ribosome Assembly	Rigid-body/Elastic network	Nanometers to hundreds of nm	Microseconds to minutes
Membrane Remodeling	Continuum/Coarse-grained	Tens of nm to micrometers	Milliseconds to seconds

Successful implementation of DFT and multiscale modeling requires specialized software tools and computational resources. The following table catalogs essential resources for researchers in this field.

Table 4: Essential Computational Resources for DFT and Multiscale Modeling

Resource Category	Specific Tools	Primary Function	Key Applications
DFT Software	Gaussian, Q-Chem, VASP, NWChem	Electronic structure calculations	Molecular properties, reaction mechanisms, spectroscopic predictions [37]
Multiscale Platforms	CHARMM, AMBER, NAMD, GROMACS	Biomolecular simulation	Enzyme mechanisms, protein folding, molecular recognition [45]
QM/MM Interfaces	ChemShell, QSite, ORCA	Hybrid quantum-classical simulations	Enzymatic reactions, catalytic mechanisms, excited states [37] [45]
Visualization Tools	VMD, Chimera, GaussView	Molecular graphics and analysis	Structure manipulation, orbital visualization, trajectory analysis [39]
Basis Sets	Pople-style, Dunning's cc-pVXZ, plane waves	Mathematical basis for wavefunction expansion	Molecular calculations (Gaussian), periodic systems (plane waves) [42]
Force Fields	CHARMM, AMBER, OPLS, Martini	Empirical potential energy functions	Biomolecular conformational sampling, coarse-grained simulations [45]

The Nobel Prize-winning advances in Density-Functional Theory and Multiscale Modeling represent pivotal achievements in the historical development of computational chemistry. DFT provided the theoretical foundation for practical electronic structure calculations across chemistry and materials science, while multiscale approaches enabled the investigation of complex biological systems operating across disparate spatial and temporal scales.

These methodologies continue to evolve through integration with machine learning approaches, enhanced computational power, and methodological refinements. Their ongoing development promises continued transformation of chemical prediction, materials design, and drug discovery, establishing computational approaches as indispensable partners to experimental investigation in advancing molecular science.

The exploration of chemical space has followed a remarkable exponential growth pattern from 1800 to 2015, with an annual production rate of new chemical compounds stable at approximately 4.4%, a trend remarkably resilient to world wars and major theoretical shifts [4]. This expansion has unfolded through three distinct historical regimes: a proto-organic period (pre-1861) characterized by uncertain year-to-year output and exploration through extraction and analysis of natural products; a more regular organic regime (1861-1980) guided by structural theory; and the current organometallic regime (post-1981), marked by the highest regularity in output [4]. Computational chemistry has been both a driver and a consequence of this exploration, evolving from theoretical concepts to an indispensable toolkit that now leverages machine learning (ML) and artificial intelligence (AI) to navigate the vastness of chemical space. This whitepaper examines how modern computational case studies in drug design, catalysis, and materials science are built upon this historical foundation, enabling researchers to solve increasingly complex problems.

Table 1: Historical Regimes in the Exploration of Chemical Space (1800-2015) [4]

Regime	Period	Annual Growth Rate (μ)	Standard Variation (σ)	Key Characteristics
Proto-organic	Before 1861	4.04%	0.4984	High variability; mix of organic, inorganic, and metal compounds; synthesis active well before Wöhler's urea synthesis.
Organic	1861–1980	4.57%	0.1251	Lower variability; structural theory guided production; C-, H-, N-, O-, and halogen-based compounds dominated.
Organometallic	1981–2015	2.96% (overall)	0.0450	Lowest variability; rise of organometallic compounds; period 1995-2015 returned to 4.40% growth.

Computational Case Studies in Drug Design

The field of drug discovery has been transformed by computational methodologies, which provide a rational framework for understanding complex biological interactions and accelerate the identification of novel therapeutics.

Field and Shape-Based Virtual Screening

Experimental Protocol: A typical workflow for identifying novel chemotypes using Cresset's Blaze software involves several key stages [46]:

• Target Preparation: Select a protein target and prepare its 3D structure, often from the Protein Data Bank (PDB).
• Ligand Preparation: Define a known active ligand or a lead series as the query molecule.
• Virtual Screening: Execute a shape and electrostatic similarity search against large compound libraries using Blaze. The software aligns candidate molecules in the database to the query based on molecular fields and shape.
• Hit Analysis: Rank the results by similarity scores and analyze the top hits for novelty and chemical diversity.
• Experimental Validation: Select chemically distinct hits for synthesis and biological testing.

Results and Impact: This approach has successfully identified nine novel chemotypes distinct from those found by traditional docking or pharmacophore methods, providing an exciting outcome for projects seeking backup series for a target [46].

Binding Pose Prediction and SAR Explanation

Experimental Protocol: To elucidate the mechanism of action of a lead series, a close collaboration between computational and medicinal chemists is essential [46]:

• Data Compilation: Gather all available Structure-Activity Relationship (SAR) data for the lead series.
• Pose Identification: Use computational experiments, including molecular docking and molecular dynamics, to identify a putative binding pose for the lead series within the target's binding site.
• Model Validation: Critically assess whether the proposed binding pose is consistent with the kinetically deduced mechanism of action (MOA) and, crucially, whether it provides a coherent explanation for the established SAR.
• Ligand Design: Apply the validated model prophetically to design new ligands with predicted improved potency or selectivity.

Results and Impact: This methodology has successfully satisfied dual goals, yielding a binding model that explains established SAR and is consistent with the kinetic MOA, thereby directly enabling the design of next-generation compounds [46].

The Scientist's Toolkit: Drug Design Research Reagents

Table 2: Key Computational Tools in Modern Drug Discovery [46] [47]

Tool / Solution	Function	Application in Case Studies
Blaze	Field and shape-based virtual screening software.	Identified 9 novel, distinct chemotypes for a backup series [46].
Electrostatic Complementarity (EC)	Proprietary technique to analyze and optimize ligand-target electrostatic interactions.	Used to identify backup series and optimize ligand binding [46].
Forge	Advanced data management, analysis, and visualization platform for molecular design.	Used to understand SAR and design future antifungal agents [46].
Molecular Modeling & Cheminformatics	A suite of techniques for predicting molecular properties, QSAR, and visualizing chemical space.	Foundational for modern drug design, teaching, and practice [47].

Computational Case Studies in Catalysis and Materials Science

Computational approaches are revolutionizing the design of catalysts and functional materials by providing atomic-level insights that are often difficult to obtain experimentally.

Machine-Learned Force Fields for Surface Science

Experimental Protocol: The application of on-the-fly machine-learned force fields (MLFFs) for studying surface properties and catalysis involves an active learning (AL) scheme to efficiently generate accurate potentials [48]:

• Active Learning Setup: Initialize a molecular dynamics (MD) simulation with a preliminary, small training set of reference structures.
• On-the-Fly Query: During the MD simulation, the MLFF algorithm continuously assesses its uncertainty for new atomic configurations encountered.
• Teacher Calculation: When uncertainty exceeds a threshold, the configuration is flagged. The "teacher" (a high-accuracy quantum mechanics method, typically Density Functional Theory (DFT)) calculates the accurate energy and forces for this structure.
• Dataset Expansion and Update: This new reference data is added to the training set, and the MLFF is retrained and updated.
• Simulation Execution: The MD simulation proceeds with the improved MLFF, now confident in the sampled region of the potential energy surface. This loop continues until the simulation is complete.

This AL scheme avoids the need for a prohibitively large, pre-computed training set by only performing costly QM calculations on-the-fly for structurally relevant configurations [48].

Results and Impact: This method has been successfully applied to examine surface properties of pristine and reconstructed surfaces of simple oxides like MgO and more complex reducible oxides like iron oxide (Fe₃O₄). It has enabled the study of system sizes, such as steps or line defects on Fe₃O₄(111), that are computationally out of reach for standard first-principles methods [48].

Digital Twin for Chemical Science

Experimental Protocol: A recent breakthrough involves creating a digital twin for chemical surface interactions, specifically for water on an Ag(111) surface [49]:

• Bidirectional Framework: Establish a real-time link between first-principles theoretical calculations and experimental characterization data (e.g., spectroscopy).
• Data Ingestion: Feed experimental spectra collected during the experiment into the digital twin.
• Model Simulation and Comparison: The digital twin runs simulations to interpret the spectroscopic data in real-time.
• Feedback and Decision-Making: The interpretation provides insights into the ongoing reaction mechanisms, enabling on-the-fly decision-making and adjustment of the experimental parameters.

Results and Impact: This framework bridges the gap between theory and experiment, allowing researchers to gain mechanistic insights based on measured spectra during the experiment itself, rather than in a post-hoc analysis [49].

Quantum Simulations of Complex Catalytic Systems

Experimental Protocol: Large-scale quantum simulations using codes like GAMESS (General Atomic and Molecular Electronic Structure System) are pushing the boundaries of what systems can be modeled [50]:

• System Construction: Build a model of a complex catalytic system, such as a silica nanoparticle surrounded by thousands of water molecules.
• Method Selection: Employ advanced quantum chemical methods, such as the effective fragment molecular orbital (EFMO) framework combined with the resolution-of-the-identity second-order Møller–Plesset perturbation (RI-MP2) method.
• Exascale Computing: Run the computation on exascale supercomputing architectures (e.g., the Aurora system), leveraging GPU offloading and linear algebra libraries.
• Analysis: Compute energies and reaction pathways for catalysis processes within the large nanoparticle.

Results and Impact: GAMESS has demonstrated the capability to model physical systems requiring chemical interactions across many thousands of atoms, indicating a new ability to model complex chemical processes relevant to heterogeneous catalysis and energy research. Performance on Aurora showed a 2.5-times improvement over other architectures [50].

The Scientist's Toolkit: Materials and Catalysis Research Reagents

Table 3: Key Computational Tools in Materials Science and Catalysis [48] [49] [50]

Tool / Solution	Function	Application in Case Studies
On-the-fly MLFF (in VASP)	Generates machine-learned force fields dynamically during MD via active learning.	Studied surface properties and water adsorption on MgO and Fe₃O₄ surfaces [48].
Digital Twin Framework	Links first-principles theory and experiment in a bidirectional feedback loop.	Enabled real-time interpretation of spectra for water interactions on Ag(111) [49].
GAMESS	A general-purpose electronic structure code for computational chemistry.	Modeled catalysis within large silica nanoparticles (1000s of atoms) [50].
PerioGT	A self-supervised deep learning framework for polymer property prediction.	Integrates periodicity priors to enhance prediction under data scarcity [49].

The historical exploration of chemical space, characterized by exponential growth and distinct evolutionary regimes, has set the stage for the current era of computational molecular science [4]. The case studies detailed herein demonstrate a powerful paradigm: the convergence of vast chemical knowledge, encoded in digital databases, with advanced computational methods like machine learning, AI, and high-performance computing. This convergence is accelerating discovery across disciplines.

Future progress will be driven by several key trends. The refinement of multi-fidelity Bayesian optimization will guide experimental campaigns more efficiently, while generative models with periodicity-aware representations will accelerate the inverse design of functional crystalline materials [49]. The push towards unified neural networks capable of modeling a wide range of solid-state materials promises to dramatically reduce computational costs and broaden the scope of designable materials [49]. Furthermore, the commitment to FAIR (Findable, Accessible, Interoperable, and Reusable) data principles in computational materials science will ensure robust, reproducible, and collaborative research, turning the collective output of the community into a continuously improving asset [51]. As these tools become more integrated and accessible, the pace of innovation in drug design, catalysis, and materials science is poised to accelerate, further expanding the mapped regions of chemical space.

Navigating Computational Challenges: Accuracy, Scalability, and Efficiency

The evolution of computational chemistry is fundamentally a history of navigating the inherent trade-off between the computational cost of simulations and the chemical accuracy of their results. From its theoretical origins in the early 20th century to its current status as an indispensable tool in drug discovery and materials science, the field's progress has been paced by breakthroughs that incrementally improved this balance [3] [9]. This technical guide examines this central challenge by tracing its historical context, detailing the quantitative metrics that define it, and providing a modern toolkit of methods and protocols that researchers can employ to optimize this critical trade-off in their own work.

The journey began with foundational theoretical work, such as that by Walter Heitler and Fritz London in 1927, who performed the first quantum mechanical calculations for a chemical system [3]. However, it was the development of computers in the 1940s and 1950s that enabled the first practical computations, such as the early semi-empirical atomic orbital calculations and the first ab initio Hartree-Fock calculations on diatomic molecules [3]. These early methods established the core paradigm: more accurate methods scale with higher computational cost, often to the power of the system size, creating a fundamental barrier for studying chemically relevant systems [3].

Table: Historical Evolution of Key Computational Methods

Time Period	Dominant Methods	Representative System Size	Key Accuracy Limitation
1950s-1960s	Semi-empirical Methods, Hückel Method	Small diatomics, conjugated hydrocarbons [3]	Empirical parameters, neglect of electron correlation [3]
1970s-1980s	Ab Initio HF, Post-HF (e.g., MP2, CI), Molecular Mechanics (e.g., MM2)	Small polyatomics (e.g., naphthalene) [3]	Hartree-Fock limit, basis set truncation [3]
1990s-Present	Density Functional Theory (DFT), Hybrid QM/MM	Medium-sized organic molecules, small proteins (with QM/MM) [3] [9]	Accuracy of exchange-correlation functional [9]
2010s-Present	Machine-Learned Interatomic Potentials (MLIPs), Ultra-Large Virtual Screening	Very large systems (thousands of atoms), billions of molecules [52] [53]	Quality and coverage of training data [53]

Quantitative Data: Accuracy vs. Cost Across Methods

The choice of computational method directly dictates the balance between achievable accuracy and the computational resources required. The following table provides a comparative overview of common methodologies, highlighting this trade-off.

Table: Computational Cost and Accuracy of Select Methods

Computational Method	Formal Scaling with System Size (N atoms)	Typical Accuracy (Energy)	Key Application Context
Molecular Mechanics (MM)	N² to N³ [3]	Not applicable to bond breaking/formation [3]	Large biomolecular systems, conformational sampling [3]
Density Functional Theory (DFT)	N³ to N⁴ [3]	3-10 kcal/mol (highly functional-dependent) [3]	Catalysis, periodic solids, medium-sized molecules [3]
Hartree-Fock (HF)	N⁴ [3]	>100 kcal/mol (due to lack of correlation) [3]	Starting point for post-HF methods [3]
MP2 (Post-HF)	N⁵ [3]	2-5 kcal/mol [3]	Non-covalent interactions, benchmark calculations [3]
Coupled Cluster (CCSD(T))	N⁷ [3]	~1 kcal/mol ("Gold Standard") [3]	High-accuracy benchmarks for small systems [3]
Machine-Learned Interatomic Potentials (MLIPs)	~N (after training) [53]	Near-DFT accuracy (training-dependent) [53]	Molecular dynamics of large, complex systems [53]

Experimental Protocols for Method Selection and Validation

Navigating the cost-accuracy landscape requires structured protocols. The following methodologies provide a roadmap for selecting and validating computational approaches for specific research goals.

Protocol for Multi-Fidelity Screening in Drug Discovery

The process of high-throughput virtual screening (HTVS) exemplifies the strategic management of computational resources. Modern pipelines often screen billions of compounds by employing a multi-stage protocol that progressively applies more accurate, but more expensive, methods to smaller subsets of molecules [54] [52].

• Library Preparation: Compile an ultralarge virtual library of readily synthesizable compounds, often in the range of 1-20 billion molecules from sources like ZINC20 or generative AI [52]. Prepare 3D structures using efficient tools like LigPrep or OMEGA.
• Triage with Fast Methods: Apply rapid, ligand-based methods such as 2D similarity searching or pharmacophore mapping to reduce the library size to millions of candidates. This step uses minimal computational cost [54].
• Structure-Based HTVS Docking: Use rapid molecular docking with a rigid receptor and a fast scoring function (e.g., Glide HTVS or AutoDock Vina) to further reduce the candidate pool to hundreds of thousands. This step incorporates the 3D structure of the target [54] [52].
• Standard-Precision (SP) Docking: Apply more computationally intensive docking protocols with flexible ligand sampling and more sophisticated scoring functions (e.g., Glide SP) to the subset from step 3, narrowing it down to thousands of hits.
• High-Precision (HP) Docking and Free Energy Perturbation (FEP): For the top few hundred candidates, use the highest accuracy docking (e.g., Glide XP) and, if necessary, ab initio methods or absolute binding free energy calculations via FEP. These methods provide near-quantitative accuracy but are reserved for a tiny fraction of the initial library due to their high cost [52].

Protocol for Developing Machine-Learned Interatomic Potentials (MLIPs)

MLIPs represent a modern solution to the cost-accuracy problem, offering near-ab initio accuracy for molecular dynamics at a fraction of the cost. The DP-GEN (Deep Potential GENerator) workflow is a robust protocol for developing reliable MLIPs [53] [55].

• Initial Ab Initio Sampling: Perform short ab initio molecular dynamics (AIMD) simulations under a range of thermodynamic conditions (e.g., temperatures from 300-1200 K) relevant to the target application. This generates an initial training set of several thousand atomic configurations, their energies, and atomic forces [55].
• MLIP Training and Exploration: Train an ensemble of four independent Deep Neural Network (DNN) models on the initial dataset. Run exploratory molecular dynamics simulations using these MLIPs.
• Active Learning and Iteration: Identify atomic configurations from the exploratory simulations where the DNN models disagree significantly. These "uncertain" snapshots are then passed back to the ab initio calculator to generate new, high-fidelity training data.
• Convergence Check and Validation: Iterate steps 2 and 3 until the MLIP model's predictions converge and show minimal disagreement across the ensemble. Validate the final MLIP against held-out AIMD data and key experimental observables (e.g., diffusivity, ionic conductivity, radial distribution functions) to ensure it captures the necessary physics [55].

MLIP Active Learning Workflow: This diagram illustrates the iterative DP-GEN process for training robust Machine-Learned Interatomic Potentials, which uses active learning to efficiently sample the configurational space [53] [55].

Success in computational chemistry relies on a suite of software, databases, and hardware that constitute the modern researcher's toolkit.

Table: Key Research Reagent Solutions in Computational Chemistry

Tool/Resource	Type	Primary Function	Relevance to Cost-Accuracy Trade-off
Gaussian	Software Package [3] [9]	Performs ab initio, DFT, and semi-empirical calculations.	The historical benchmark; allows direct selection of method and basis set to manage cost vs. accuracy [3].
BindingDB	Database [3]	Repository of experimental protein-small molecule interaction data.	Provides critical experimental data for validating and improving the accuracy of computational predictions [3].
AlphaFold2	AI Software [54]	Predicts 3D structures of proteins from amino acid sequences.	Drastically reduces cost and time of obtaining protein structures for SBDD, though model accuracy can vary [54].
GPU Accelerators	Hardware	Specialized processors for parallel computation.	Critical for reducing the wall-clock time of expensive calculations like MD, FEP, and ML model training [52].
ZINC20/Enamine REAL	Database [52]	Ultralarge libraries of commercially available or readily synthesizable compounds.	Provides the chemical space for virtual screening, enabling the shift from HTS to HTVS for efficient lead discovery [52].
Molecular Docking Software (e.g., Glide, AutoDock)	Software Package [54] [52]	Predicts the binding pose and affinity of a small molecule to a macromolecular target.	Enables rapid structure-based screening of billions of molecules, with tiered accuracy levels (HTVS/SP/XP) [54].

Visualization of Method Hierarchies and Workflows

Understanding the relationships between different computational methods and their typical applications is key to strategic planning. The following diagram maps this landscape.

Computational Method Selection Guide: This diagram assists in selecting a computational method based on the target property of interest and the required balance between system size and computational cost.

The challenge of accurately describing systems of many interacting quantum particles constitutes one of the most enduring and computationally demanding problems in theoretical chemistry and physics. Termed the "quantum many-body problem," its core difficulty stems from the exponential growth of computational resources required to model quantum systems as their size increases. This challenge is particularly acute in addressing electron correlation—the fact that the motion of each electron in a molecule or material is influenced by the instantaneous positions of all other electrons, rather than merely moving in an average field [56]. The historical development of computational chemistry from 1800 to 2015 represents a sustained effort to tame this complexity, moving from empirical observations to increasingly sophisticated theoretical models capable of predicting chemical behavior from first principles.

The significance of solving this problem can scarcely be overstated. Understanding electron correlation is essential for predicting chemical reaction rates, explaining spectroscopic phenomena, designing novel materials with tailored properties, and accelerating drug discovery by accurately modeling molecular interactions [56] [57]. The journey began with early quantum theory in the 1920s and has progressed through a series of methodological revolutions, each extending the frontier of what systems could be treated with quantitative accuracy. This whitepaper examines the key strategic approaches that have been developed to solve the quantum many-body problem, places them in their historical context, and explores the emerging paradigms that promise to extend these capabilities further.

Historical Context: The Evolution of Computational Quantum Chemistry

The formal foundation for quantum chemistry was laid with the work of Heitler and London in 1927, who performed the first quantum mechanical treatment of a chemical bond in the hydrogen molecule [3]. The subsequent decades witnessed the development of two fundamental theoretical frameworks: valence bond theory and molecular orbital theory. However, the practical application of these theories to molecules beyond the simplest cases required the advent of digital computers in the 1950s. A significant milestone was marked by Clemens C. J. Roothaan's 1951 paper, which systematized the Linear Combination of Atomic Orbitals Molecular Orbitals (LCAO MO) approach [3]. The first ab initio Hartree-Fock calculations on diatomic molecules were performed at MIT in 1956, utilizing a basis set of Slater orbitals [3].

The growth of chemical knowledge and computational capability has been exponential. An analysis of the Reaxys database, encompassing over 14 million compounds reported from 1800 to 2015, reveals that the annual number of new compounds grew at a stable rate of 4.4% over this 215-year period, a trend surprisingly resilient even to world wars [4]. This exploration occurred in three distinct historical regimes, each with characteristic growth rates and variability in annual output, as detailed in Table 1.

Table 1: Historical Regimes in the Exploration of Chemical Space (1800-2015)

Regime/Period	Time Span	Annual Growth Rate (μ)	Standard Variation (σ)	Key Characteristics
Proto-organic	Before 1861	4.04%	0.4984	High variability; mix of natural product extraction and early synthesis; dominated by C, H, N, O, halogen compounds [4].
Organic	1861–1980	4.57%	0.1251	Guided by structural theory; synthesis becomes established as the primary method for new compounds [4].
Organometallic	1981–2015	2.96%	0.0450	Most regular output; focus on organometallic and coordination compounds [4].
WW1	1914–1918	-17.95%	0.0682	Sharp production decline due to global conflict [4].
WW2	1940–1945	-6.00%	0.0745	Production decline, less severe than WW1 [4].

The 1970s marked the crystallization of computational chemistry as a distinct discipline, facilitated by the development of efficient ab initio programs like Gaussian [3]. The field received Nobel recognition in 1998, when Walter Kohn was honored for developing Density Functional Theory (DFT) and John Pople for his development of computational methods in quantum chemistry [3]. This historical progression sets the stage for understanding the specific strategies developed to solve the electron correlation problem.

Theoretical Foundations of Electron Correlation

In quantum chemistry, the electronic wave function describes the behavior of all electrons in a system. The Hartree-Fock (HF) method approximates this complex many-electron wave function as a single Slater determinant of molecular orbitals. While HF provides a good starting point, it fails to capture electron correlation, defined as the difference between the exact solution of the non-relativistic Schrödinger equation and the HF result [56]. The correlation energy, a term coined by Löwdin, is crucial for achieving "chemical accuracy" (errors < 1 kcal/mol) [56].

Electron correlation is conceptually divided into two types:

• Dynamical Correlation: This arises from the instantaneous Coulombic repulsion between electrons, which keeps them apart. It is a short-range effect and is responsible for chemically important phenomena like London dispersion forces [56].
• Non-Dynamical (Static) Correlation: This occurs when a system's ground state is intrinsically multi-configurational and cannot be described by a single dominant Slater determinant without significant errors. This is common in bond-breaking situations, transition metal complexes, and diradicals [56].

The following diagram illustrates the logical relationship between the core problem and the various methodological strategies developed to solve it.

Diagram 1: Strategies for the Quantum Many-Body Problem

Classical Computational Strategies

Post-Hartree-Fock Wave Function Methods

These methods build upon the HF wave function to recover correlation energy by including excited configurations.

4.1.1 Configuration Interaction (CI) The CI method expresses the correlated wave function as a linear combination of the ground-state HF determinant and excited determinants (single, double, triple, etc., excitations) [58]: [ \psi{\text{CI}} = C0 \Phi{\text{HF}} + \sum{i,a} Ci^a \Phii^a + \sum{i>j, a>b} C{ij}^{ab} \Phi{ij}^{ab} + \cdots ] where ( \Phii^a ) is a singly excited determinant, and so on. While conceptually straightforward, full CI (including all excitations) is computationally intractable for all but the smallest systems. In practice, the expansion is truncated, typically at single and double excitations (CISD). A major bottleneck is the transformation of two-electron integrals from the atomic orbital to the molecular orbital basis, which scales as the fifth power of the number of basis functions [58].

4.1.2 Coupled Cluster (CC) Theory Coupled cluster theory employs an exponential ansatz for the wave function: ( \psi{\text{CC}} = e^{\hat{T}} \Phi{\text{HF}} ), where ( \hat{T} = \hat{T}1 + \hat{T}2 + \hat{T}_3 + \cdots ) is the cluster operator representing single, double, triple, etc., excitations [57]. The inclusion of approximate triple excitations, as in the CCSD(T) method, is often considered the "gold standard" of quantum chemistry for small molecules, providing high accuracy but at a very high computational cost that scales steeply with system size [57].

4.1.3 Perturbation Theory Møller-Plesset perturbation theory treats electron correlation as a perturbation to the HF Hamiltonian. The second-order correction (MP2) is widely used due to its favorable scaling, but it is not variational, meaning the calculated energy is not guaranteed to be an upper bound to the exact energy [56].

4.1.4 Multi-Reference Methods For systems with strong static correlation, multi-configurational self-consistent field (MCSCF) methods like Complete Active Space SCF (CASSCF) are employed. These methods optimize both the CI coefficients and the molecular orbitals for a set of key (active space) configurations. Dynamical correlation can then be added on top via multi-reference perturbation theory (e.g., CASPT2) or multi-reference CI [56].

Table 2: Comparison of Key Post-Hartree-Fock Electronic Structure Methods

Method	Key Principle	Scaling	Strengths	Weaknesses
Configuration Interaction (CISD)	Linear combination of HF + excited determinants [58].	N⁶	Size-consistent for full CI; variational.	Not size-consistent when truncated; high memory cost.
Coupled Cluster (CCSD(T))	Exponential wave function ansatz [57].	N⁷	High "gold standard" accuracy; size-consistent.	Very high computational cost; limited to small molecules.
Møller-Plesset (MP2)	2nd-order perturbation theory [56].	N⁵	Good cost/accuracy for dynamical correlation.	Not variational; poor for static correlation.
CASSCF	Multi-configurational wave function in an active space [56].	Exponential in active space	Excellent for static correlation, bond breaking.	Limited by active space size; misses dynamical correlation.

Density Functional Theory (DFT) and its Hybrids

As an alternative to wave function-based methods, DFT formulates the problem in terms of the electron density rather than the wave function. According to the Hohenberg-Kohn theorems, the ground-state energy is a unique functional of the electron density [3]. In practice, the unknown exchange-correlation functional must be approximated. The success of DFT stems from its favorable N³ scaling, allowing it to be applied to much larger systems than post-HF methods.

Modern DFT strategies often employ hybrid functionals, which mix a portion of exact HF exchange with DFT exchange and correlation. While highly efficient, the accuracy of DFT is inherently limited by the quality of the approximate functional, particularly for dispersion-bound systems, transition metals, and strongly correlated materials.

The Scientist's Toolkit: Key Research Reagents and Computational Solutions

Table 3: Essential "Reagents" for Computational Electron Correlation Studies

Research Reagent / Method	Function in the Computational Experiment
Gaussian-type Orbitals (GTOs)	Basis functions used to expand molecular orbitals; the choice of basis set size and quality is critical for convergence [3].
Slater-type Orbitals (STOs)	More physically correct basis functions; computationally more expensive to integrate than GTOs [3].
Pseudopotentials (PPs)	Replace core electrons with an effective potential, reducing the number of electrons to be treated explicitly [3].
Coupled-Cluster with Single, Double, and Perturbative Triple Excitations (CCSD(T))	Provides a high-accuracy benchmark for calculating correlation energy in small molecules [57].
Density Functional Theory (DFT)	Workhorse method for calculating electronic structure of large molecules and solids via the electron density [3].
Multi-task Electronic Hamiltonian Network (MEHnet)	A neural network architecture trained on CCSD(T) data to predict multiple electronic properties with high accuracy and speed [57].

Emerging Paradigms: Machine Learning and Quantum Computing

Machine Learning in Electronic Structure

A groundbreaking approach involves using machine learning (ML) to bypass the high cost of accurate quantum chemistry methods. Recently, MIT researchers developed the Multi-task Electronic Hamiltonian network (MEHnet), a neural network with a novel E(3)-equivariant graph neural network architecture [57]. This model is trained on high-quality CCSD(T) calculations but can subsequently perform calculations at speeds far exceeding traditional methods. Crucially, MEHnet can predict multiple electronic properties—such as dipole moments, polarizability, and excitation gaps—from a single model, and can handle both ground and excited states [57]. This represents a significant strategic shift from calculating properties from first principles to learning them from high-quality data and generalizing to new molecules.

The workflow for this ML-accelerated strategy is illustrated below.

Diagram 2: Machine Learning for Electronic Structure

Quantum Computing for Quantum Chemistry

Quantum computing offers a fundamentally new strategy for the many-body problem by using a controllable quantum system to simulate another. A key metric is "nonstabilizerness" or "magic," a resource necessary for quantum computers to surpass classical systems [59]. The fundamental advantage is that the state space of a quantum computer grows exponentially with the number of qubits, naturally mimicking the exponential complexity of many-body quantum systems.

Specialized algorithms have been developed for quantum computers, including the Variational Quantum Eigensolver (VQE) and the Quantum Phase Estimation (QPE) algorithm, which are designed to find the ground-state energy of molecular systems. Recent breakthroughs in 2025, such as Google's Willow chip with 105 superconducting qubits, have demonstrated exponential error reduction, a critical step towards fault tolerance [60]. Applications in drug discovery are already emerging; for instance, Google's collaboration with Boehringer Ingelheim simulated the Cytochrome P450 enzyme with greater efficiency than classical methods [60]. The hardware roadmap is aggressive, with IBM targeting quantum-centric supercomputers with 100,000 qubits by 2033 [60].

Table 4: Emerging Paradigms for Tackling Electron Correlation

Paradigm	Representative Example	Reported Performance/Progress	Potential Application
Machine Learning Force Fields	MEHnet (MIT) [57].	CCSD(T)-level accuracy for systems of thousands of atoms at reduced computational cost.	High-throughput screening of molecules and materials; drug design [57].
Quantum Algorithm Execution	Variational Quantum Eigensolver (VQE) on IonQ 36-qubit computer [60].	Medical device simulation outperformed classical HPC by 12% [60].	Quantum chemistry simulation of catalysts and active sites [60].
Quantum Error Correction	Google's Willow chip (105 qubits) [60].	Achieved exponential error reduction ("below threshold"); completed a calculation in ~5 mins that would take a classical supercomputer 10^25 years [60].	Enabling larger, more accurate quantum simulations by mitigating decoherence.
Hybrid Quantum-Classical	IBM's Quantum-HPC integration [60].	Roadmap for systems combining quantum processors with classical co-processors.	Near-term practical applications leveraging strengths of both paradigms.

The quest to solve the quantum many-body problem and accurately model electron correlation has been a driving force in the development of computational chemistry for nearly a century. The historical trajectory has progressed from foundational quantum mechanics to the development of sophisticated, layered computational strategies like post-Hartree-Fock methods and DFT. The strategic landscape is now diversifying dramatically. While classical methods continue to advance through clever algorithms and machine-learning acceleration, the emergence of quantum computing offers a transformative, if longer-term, path forward. The ultimate "taming of complexity" will likely not come from a single strategy but from a synergistic combination of all these approaches: classical computation for system design and validation, machine learning for rapid screening and property prediction, and quantum computation for the most challenging correlated systems intractable by any other means. This multi-pronged attack on one of chemistry's most fundamental problems promises to unlock new frontiers in drug discovery, materials science, and our basic understanding of molecular phenomena.

The field of computational chemistry has evolved dramatically over the past two centuries, transitioning from early empirical observations to sophisticated multi-scale simulations. Analysis of chemical discovery from 1800 to 2015 reveals distinct historical regimes characterized by exponential growth in reported compounds at approximately 4.4% annually, a trend remarkably consistent despite world events and theoretical shifts [4]. This systematic exploration of chemical space established the foundational knowledge necessary for today's computational approaches. The development of quantum mechanics/molecular mechanics (QM/MM) methodologies represents a pivotal convergence of theoretical physics, chemistry, and computational science, enabling researchers to model complex biological systems with unprecedented accuracy. Introduced in 1976 by Warshel and Levitt, with Karplus later contributing significantly to its development, this hybrid approach earned its creators the 2013 Nobel Prize in Chemistry for "the development of multiscale models for complex chemical systems" [61] [62]. This recognition underscores the transformative impact of QM/MM methods in bridging the gap between quantum-level precision and macromolecular complexity, particularly for biological applications including enzymatic mechanisms and drug design.

Historical Development and Theoretical Foundations

The Evolution of Computational Chemistry

The progression toward QM/MM methods unfolded alongside key developments in computational chemistry throughout the 20th century. Following the first theoretical chemistry calculations by Heitler and London in 1927, the field advanced significantly with the emergence of digital computing in the 1950s [3]. The 1960s witnessed two critical developments: Kohn's formulation of density-functional theory (DFT) and Pople's creation of the Gaussian program for quantum mechanical calculations [3] [9]. These innovations addressed the fundamental challenge in computational chemistry: the prohibitive cost of applying quantum mechanical methods to large systems. While quantum mechanics (QM) offers high accuracy for modeling electron dynamics during chemical reactions, its computational requirements scale poorly with system size. Conversely, molecular mechanics (MM) uses classical Newtonian physics to efficiently simulate large biomolecules but cannot model bond formation or cleavage [61]. The QM/MM approach elegantly resolves this dichotomy by partitioning the system, applying accurate QM methods to the chemically active region (e.g., an enzyme active site) while treating the surrounding environment with computationally efficient MM [62].

Table: Historical Regimes of Chemical Discovery (1800-2015)

Regime	Period	Annual Growth Rate	Key Characteristics
Proto-organic	Before 1861	4.04%	High variability in year-to-year output; mix of organic and inorganic compounds with significant metal-containing compounds
Organic	1861-1980	4.57%	More regular production; dominance of carbon- and hydrogen-containing compounds (>90% after 1880)
Organometallic	1981-2015	2.96% (1981-1994); 4.40% (1995-2015)	Most regular output; revival in metal-containing compounds discovery

Source: Adapted from Llanos et al. [4]

Fundamental QM/MM Methodologies

The theoretical framework of QM/MM involves several critical methodological considerations. The total energy of the combined QM/MM system is typically calculated using an additive approach:

The interaction energy between QM and MM regions comprises electrostatic, van der Waals, and bonded terms [61]. Three primary embedding schemes dictate how these interactions are handled:

• Mechanical Embedding: Treats QM-MM interactions entirely at the MM level, neglecting polarization effects on the QM region [61].
• Electrostatic Embedding: Includes the electrostatic potential of MM partial charges in the QM Hamiltonian, allowing polarization of the QM region by the MM environment [61].
• Polarized Embedding: Allows mutual polarization between QM and MM regions, providing the most physically accurate but computationally demanding approach [61].

Table: QM/MM Embedding Schemes Comparison

Embedding Type	Polarization of QM System	Polarization of MM System	Computational Cost	Typical Applications
Mechanical	No	No	Low	Simple systems where charge transfer is negligible
Electrostatic	Yes	No	Medium	Most biomolecular applications
Polarized	Yes	Yes	High	Systems where MM environment polarization is critical

For systems where the QM/MM boundary passes through covalent bonds, specialized boundary treatments are essential. The link atom approach introduces hydrogen atoms to cap dangling bonds of QM atoms [61]. Alternative methods include boundary atom schemes that use specialized atoms participating in both QM and MM calculations, and localized-orbital schemes that employ hybrid orbitals at the boundary [61].

QM/MM Methodologies and Technical Implementation

Computational Efficiency and Advanced Sampling

A primary advantage of QM/MM methods is their computational efficiency. While pure QM methods typically scale between O(N³) to O(N²˙⁷), where N represents the number of basis functions, MM methods scale between O(N) to O(N²) with the number of atoms [61]. QM/MM achieves an optimal balance by restricting computationally intensive QM calculations to the chemically relevant region. To further enhance efficiency, many implementations employ a multi-layered spherical approach for evaluating QM-MM electrostatic interactions: MM atoms in the innermost sphere interact directly with the QM electron density, those in the middle sphere interact with the QM multipole moments, and atoms in the outermost sphere interact with the partial charges of the polarized QM region [61].

Despite these efficiency improvements, adequate sampling of conformational space remains challenging. Standard QM/MM molecular dynamics simulations are often limited to picosecond timescales, insufficient for probing enzymatic reactions typically occurring on microsecond to millisecond timescales. Consequently, researchers employ enhanced sampling techniques including Blue Moon Ensemble, metadynamics, and string methods to calculate free energy profiles and reaction mechanisms [63] [64]. These approaches enable more efficient exploration of the potential energy surface, providing statistically meaningful results for complex biochemical processes.

Density Functional Theory in QM/MM Simulations

The choice of quantum mechanical method significantly impacts QM/MM simulation accuracy and efficiency. Density Functional Theory (DFT) has emerged as a particularly valuable QM component due to its favorable balance between accuracy and computational cost [62] [63]. Unlike wavefunction-based methods that compute the full N-electron wavefunction, DFT determines the total electronic energy via the electron density distribution, inherently including electron correlation effects [62]. Modern DFT implementations employ increasingly sophisticated functionals:

• Generalized Gradient Approximation (GGA): Improves upon Local Density Approximation by including electron density gradient terms (e.g., BLYP functional) [62].
• Hybrid Functionals: Incorporate a portion of exact Hartree-Fock exchange (e.g., B3LYP with 20% HF exchange) [62].
• Range-Separated and Specialized Functionals: Address specific challenges like long-range interactions (e.g., LC-wPBE, CAM-B3LYP) or biochemical systems (e.g., MN15) [62].

For processes involving electronic excitations, such as photosynthesis, Time-Dependent DFT (TD-DFT) extends conventional DFT to model excited states [62]. The integration of DFT within QM/MM frameworks has been particularly impactful for studying metalloenzymes, where the electronic structure of transition metal clusters directly governs catalytic function [62] [63].

Applications in Biological Systems

Enzymatic Reaction Mechanisms

QM/MM methods have revolutionized computational enzymology by enabling detailed investigation of reaction mechanisms in their native protein environments. Studies of chorismate mutase exemplify this approach, where multiple QM/MM studies have revealed how the enzyme stabilizes the transition state and accelerates the Claisen rearrangement [63]. Similarly, QM/MM simulations have elucidated catalytic mechanisms in cytochrome P450 enzymes, revealing a two-state rebound mechanism for C-H hydroxylation and the role of peripheral heme substituents in controlling hydrogen-atom abstraction [63]. These insights extend to medically relevant systems, including β-lactamase enzymes responsible for antibiotic resistance, where QM/MM studies have detailed the acylation and deacylation steps underlying resistance mechanisms [63].

The workflow for enzymatic QM/MM investigations typically begins with experimental structural data from the Protein Data Bank, followed by system preparation and partitioning into QM and MM regions. The reaction pathway is then explored using potential energy surfaces and free energy sampling techniques [63] [64]. This integrated approach has become sufficiently accurate for meaningful comparison with experimental data, positioning QM/MM simulations as predictive tools complementing traditional laboratory experiments.

Drug Discovery and Design

In pharmaceutical research, QM/MM approaches contribute significantly to understanding drug action and optimizing therapeutic compounds. Applications include modeling drug-receptor interactions at quantum mechanical accuracy, predicting metabolic transformation pathways, and designing targeted inhibitors [63]. For example, QM/MM studies of fatty acid amide hydrolase (FAAH) have elucidated hydrolysis mechanisms for endogenous cannabinoids, informing the development of potential therapeutic inhibitors [63]. The ability to model complete enzymatic reaction pathways with chemical accuracy allows researchers to predict drug metabolism and toxicity profiles before extensive laboratory testing [63].

Recent advances combine QM/MM with automated molecular docking and free energy perturbation calculations, creating powerful pipelines for structure-based drug design. These multi-scale approaches efficiently leverage HPC facilities to screen compound libraries, optimize lead structures, and predict binding affinities with remarkable accuracy [64]. As QM/MM methodologies continue evolving alongside computing capabilities, their impact on rational drug design is expected to grow substantially.

Research Reagent Solutions

Table: Essential Computational Tools for QM/MM Research

Resource	Type	Primary Function	Key Features
CPMD [64]	Software Package	Ab initio molecular dynamics	Plane wave/pseudopotential DFT; QM/MM functionality; parallel efficiency
CP2K [64]	Software Suite	Atomistic simulations of condensed systems	Hybrid Gaussian/plane wave DFT; QM/MM; advanced sampling
Gaussian [3] [9]	Quantum Chemistry Program	Electronic structure calculations	Extensive method/basis set library; versatile QM/MM capabilities
PDB [64]	Database	Experimental structural data	Repository for biomolecular structures; starting point for simulations
CECAM [64]	Research Center	Training and workshops	QM/MM methodology schools; community development

The continued evolution of QM/MM methodologies focuses on enhancing accuracy, efficiency, and applicability. Key development areas include: (1) implementing high-level ab initio correlation methods (e.g., coupled cluster theory) for improved energetic predictions [63]; (2) refining polarizable force fields to better represent MM region polarization [61] [62]; (3) optimizing algorithms for emerging exascale computing architectures [64]; and (4) developing more sophisticated sampling techniques to address complex conformational changes in biomolecules [63]. These advances will further solidify QM/MM as an indispensable tool for studying biological systems.

The development of QM/MM methods represents a natural evolution within the broader historical context of chemical exploration. Just as the systematic investigation of chemical space progressed through distinct regimes from 1800 to 2015 [4], computational chemistry has matured from fundamental quantum mechanical calculations to sophisticated multi-scale modeling. The 2013 Nobel Prize awarded for QM/MM methodologies acknowledges their transformative role in bridging theoretical chemistry and biological complexity [62]. As these methods continue to advance alongside computational hardware, QM/MM simulations will play an increasingly central role in biochemical research, drug discovery, and materials science, enabling unprecedented atomic-level insight into complex molecular processes within biologically relevant environments.

The field of computational chemistry has been shaped by a continuous and dynamic coevolution between hardware capabilities and software algorithms. This partnership, driven by the need to solve increasingly complex chemical problems, has transformed computational chemistry from a specialized theoretical endeavor into a central methodology alongside experiment and theory [65]. The exploration of chemical space has grown exponentially since 1800, with an annual growth rate of 4.4% in the reporting of new compounds, a trend that has persisted through scientific revolutions and global conflicts alike [4]. This relentless expansion has consistently demanded more computational power and more sophisticated algorithms. From the early supercomputers of the 1960s to today's exascale systems and emerging quantum processors, each hardware advancement has created opportunities for new algorithmic approaches, which in turn have pushed the boundaries of what is computationally feasible [66] [67]. This whitepaper examines this coevolutionary process, detailing how the synergistic development of hardware and software has enabled computational chemistry to progress through distinct historical regimes, each characterized by new capabilities and scientific insights.

Historical Evolution of Computational Chemistry

The development of computational chemistry reflects a journey through three distinct historical regimes, each characterized by specific patterns in the exploration of chemical space and supported by contemporary computing capabilities.

The Three Regimes of Chemical Exploration

Analysis of millions of reactions stored in the Reaxys database reveals that the production of new chemical compounds from 1800 to 2015 followed three statistically distinguishable historical regimes, characterized by different growth rates and variability in annual compound production [4].

Table 1: Historical Regimes in Chemical Exploration (1800-2015)

Regime	Period	Annual Growth Rate (μ)	Variability (σ)	Key Characteristics
Proto-organic	Before 1861	4.04%	0.4984	High variability, mix of organic and inorganic compounds, synthesis already established
Organic	1861-1980	4.57%	0.1251	More regular production, dominated by C-, H-, N-, O-, and halogen-based compounds
Organometallic	1981-2015	2.96% (1981-1994: 0.079%; 1995-2015: 4.40%)	0.0450	Most regular regime, dominated by organometallic compounds

The Proto-organic regime before 1861 was characterized by high year-to-year variability in the output of new compounds. During this period, chemistry was primarily exploratory, with chemists relying on extraction from natural sources and increasingly using synthesis to produce new compounds, contrary to the belief that synthesis only became important after Wöhler's 1828 urea synthesis [4]. The Organic regime (1861-1980) emerged with the establishment of structural theory, leading to a century of more regular and guided production of organic compounds. The current Organometallic regime (1981-present) exhibits the most regular output, focusing on organometallic compounds and enabled by sophisticated computational methods [4].

Hardware Evolution and Its Impact

The hardware available in each of these regimes fundamentally shaped the computational approaches possible. In the 1960s, supercomputers like the CDC 6600, designed by Seymour Cray, used silicon transistors and introduced refrigeration to solve overheating problems [67]. The 1970s saw the rise of vector processors like the Cray-1, which became one of the most successful supercomputers in history [67]. The transition to massively parallel systems in the 1990s, with tens of thousands of commodity processors, marked another paradigm shift, enabling computational chemists to tackle larger systems with greater accuracy [65] [67].

This hardware evolution directly facilitated the growth depicted in Table 1. As noted by Peter Taylor in a 1999 National Research Council workshop, "computational chemists have been among the foremost users of computer hardware, with substantial requirements for computer time, memory, and disk space, and with a history of exploiting both early access to new architectures and novel solutions to reduce the cost of performing their research" [65].

Figure 1: Historical regimes of chemical exploration and corresponding hardware evolution

Modern Computational Frameworks

Algorithmic Complexity in Classical Computational Chemistry

The coevolution of hardware and software is perhaps most evident in the development of computational chemistry algorithms with varying complexity and accuracy trade-offs. As hardware capabilities expanded, increasingly sophisticated algorithms became feasible, enabling higher accuracy calculations for larger molecular systems.

Table 2: Classical and Quantum Algorithm Complexities for Computational Chemistry

Method	Classical Time Complexity	Representative Accuracy	Quantum Advantage Timeline (QPE)	Key Applications
Density Functional Theory (DFT)	O(N³)	Variable, depends on functional	>2050	Large systems, materials science
Hartree Fock (HF)	O(N⁴)	Low (no correlation energy)	>2050	Starting point for higher accuracy methods
Møller-Plesset Second Order (MP2)	O(N⁵)	Moderate	2038	Incorporating electron correlation
Coupled Cluster Singles and Doubles (CCSD)	O(N⁶)	High	2036	Accurate thermochemistry
Coupled Cluster Singles and Doubles with Perturbative Triples (CCSD(T))	O(N⁷)	Very high ("gold standard")	2034	Benchmark quality calculations
Full Configuration Interaction (FCI)	O*(4^N)	Exact (within basis set)	2031	Small system benchmarks

The progression from Hartree Fock to Full Configuration Interaction represents a trade-off between computational cost and accuracy. As noted in recent research, "While many biological systems can be treated with lower-accuracy methods, numerous important drug complexes and enzymes exhibit strong electronic correlation, especially those with transition metal centers" [68]. This drives the need for both improved algorithms and more powerful hardware.

The Shift to Codesign and Coevolution

The relationship between hardware and software has evolved from simple porting of existing algorithms to new architectures to a sophisticated codesign approach where algorithms and hardware are developed synergistically. The redesign of NWChem into NWChemEx exemplifies this modern codesign philosophy, explicitly considering emerging exascale computer architectures during method development [66].

This coevolution extends to quantum computing, where researchers are developing "software-hardware co-optimization for computational chemistry on superconducting quantum processors" [69]. By coordinating optimization objectives through Pauli strings—the basic building blocks of computational chemistry programs—researchers can identify critical program components for compression and tailor novel hardware architectures specifically for chemistry simulations [69].

Recent research from Google and Rice University demonstrates how this coevolution can overcome technological plateaus. Google developed reinforcement learning techniques to automate chip floorplanning, producing optimized layouts in hours instead of months [70]. Meanwhile, Rice University researchers optimized AI algorithms for commodity CPUs, achieving 15 times faster training of deep neural networks compared to GPU-based platforms [70]. Together, these approaches demonstrate a future where hardware and algorithms are developed seamlessly in parallel.

Experimental Protocols and Methodologies

Software-Hardware Co-Optimization for Quantum Chemistry

Objective: To implement and validate a co-optimized approach for computational chemistry simulations on superconducting quantum processors by simultaneously optimizing application, compiler, and hardware components [69].

Methodology:

• Program Analysis: Decompose target chemistry Hamiltonians into Pauli strings, the fundamental building blocks of quantum computational chemistry programs.
• Critical Component Identification: Apply compression algorithms to identify program components that can be simplified with minimal accuracy loss, focusing on the structure of Pauli string simulation circuits.
• Hardware Tailoring: Design novel hardware architectures specifically optimized for executing the identified critical Pauli string patterns.
• Compiler Development: Implement specialized compilation techniques that translate chemistry problems into quantum circuits optimized for the target hardware.
• Validation: Benchmark simulation accuracy and execution overhead against classical methods and uncompressed quantum approaches.

Key Parameters: Execution overhead reduction, quantum circuit depth, quantum volume requirements, algorithmic accuracy preservation.

This methodology has demonstrated execution overhead reduction of up to 99% compared to non-optimized approaches, highlighting the significant potential of hardware-algorithm coevolution in quantum computational chemistry [69].

Variational Quantum Algorithms for Grid-Based Dynamics

Objective: To simulate quantum dynamics in first quantization using variational quantum algorithms that overcome limitations of Trotterized approaches while reducing measurement requirements [71].

Methodology:

• System Encoding: Map the chemical system to a grid-based representation in first quantization, enabling direct simulation of quantum dynamics.
• Ansatz Selection: Employ heuristic variational forms tailored to molecular systems, bypassing the difficult decomposition of Trotterized first quantized Hamiltonians into quantum gates.
• Measurement Optimization: Leverage the grid encoding property that requires measurement only in position and momentum bases, irrespective of system size, addressing the high measurement cost typically associated with variational approaches.
• Subspace Diagonalization: Implement subspace diagonalization to attenuate numerical instabilities in variational time propagation at a cost of O(MN²) 2-qubit gates, where M is the number of dimensions and N^M is the total number of grid points.
• Dynamics Simulation: Apply the optimized variational algorithm to study systems in one and two dimensions, comparing results with classical benchmark methods.

Validation Metrics: State fidelity, energy conservation, computational resource requirements, scalability with system size [71].

Figure 2: Hardware-software codesign methodology for computational chemistry

The Scientist's Toolkit: Essential Research Reagents

Modern computational chemistry relies on a sophisticated toolkit of software, hardware, and methodological approaches that enable the exploration of chemical space. This toolkit has evolved significantly from the early days of manual calculations to today's integrated software-hardware ecosystems.

Table 3: Essential Computational Chemistry Tools and Their Functions

Tool Category	Specific Technologies/Approaches	Function	Hardware Requirements
Electronic Structure Software	NWChemEx [66], Quantum ESPRESSO, Gaussian	Calculate molecular properties, reaction pathways, and dynamics	Massively parallel supercomputers, exascale systems
Quantum Computing Frameworks	Variational Quantum Algorithms [71], Quantum Phase Estimation [68]	Solve quantum systems intractable for classical computers	Superconducting quantum processors with error correction
Specialized Hardware	Tensor Processing Units (TPUs) [70], GPUs, CPUs with hash table optimization [70]	Accelerate specific computational patterns (matrix multiplication, search problems)	Custom AI accelerators, commodity hardware with optimized algorithms
Interconnect Technologies	InfiniBand, 3D Torus Networks [67]	Enable communication between processors in parallel systems	High-speed, low-latency networking for massively parallel systems
Data Analysis & Visualization	Reaxys database analysis [4], Molecular visualization tools	Extract patterns from chemical data, visualize molecular structures	Large-memory systems for handling billions of chemical reactions

The toolkit reflects the coevolutionary nature of the field. As expressed by Peter Taylor, "Efforts are needed to increase the accuracy of our results and to achieve that accuracy for larger and larger systems, to model experiments more realistically, and to develop software appropriate to new hardware so as to fulfill the opportunities offered by ASCI-class machines" [65]. This perspective underscores the continuous interplay between tool development and scientific advancement.

Future Directions and Quantum Computational Chemistry

The hardware-software coevolution continues with the emergence of quantum computing for chemical simulations. Research indicates that quantum computers will likely make their earliest contributions in specific, high-accuracy domains rather than immediately supplanting all classical methods.

Projected Quantum Advantage Timeline

Based on current development trajectories, quantum phase estimation (QPE) is expected to surpass highly accurate classical methods for small to medium-sized molecules in the coming decade [68]:

• Full Configuration Interaction (FCI): Quantum advantage projected by ~2031
• Coupled Cluster Singles and Doubles with Perturbative Triples (CCSD(T)): ~2034
• Coupled Cluster Singles and Doubles (CCSD): ~2036
• Møller-Plesset Second Order (MP2): ~2038

This timeline suggests that quantum computing will initially complement rather than replace classical approaches. As noted in recent research, "in the next decade or so, quantum computing will be most impactful for highly accurate computations with small to medium-sized molecules, whereas classical computers will likely remain the typical choice for calculations of larger molecules" [68].

Targeted Applications for Quantum Advantage

Quantum computational chemistry is particularly promising for specific challenging chemical systems:

• Transition Metal Complexes: Systems like nitrogen-fixing enzymes (FeMo cofactor) and cytochrome P450 with iron centers exhibit strong electronic correlations that challenge classical methods [68].
• Homogeneous Catalysis: Quantum computers could accelerate catalyst discovery, particularly for complexes with strong correlation effects [68] [72].
• Strongly Correlated Materials: Systems described by the Fermi-Hubbard model may benefit from quantum simulations, though further hardware advances are necessary [67].

The hardware-software coevolution continues to be essential in the quantum realm. As researchers note, "While exploiting the high-level domain knowledge reveals significant optimization opportunities, our hardware/software framework is not tied to a particular program instance and can accommodate the full family of computational chemistry problems with such structure" [69]. This flexibility will be crucial as quantum hardware matures and new algorithmic paradigms emerge.

The historical development of computational chemistry from 1800 to the present demonstrates a consistent pattern of hardware-software coevolution driving scientific progress. From the proto-organic regime of the 19th century to the current organometallic regime, each phase of chemical exploration has been enabled by contemporary computational capabilities [4]. The field has progressed from specialized quantum chemistry calculations on early supercomputers to sophisticated codesign approaches that simultaneously optimize algorithms and hardware architectures [66] [69].

This coevolutionary process has transformed computational chemistry into what Peter Taylor described as "one of the great scientific success stories of the past decades," evolving from a specialist activity to a fundamental methodology alongside experiment and theory [65]. As the field advances toward exascale computing and practical quantum advantage, the continued synergy between hardware innovation and algorithmic development will be essential for addressing outstanding challenges in accuracy, system size, and simulation time scales. The future of computational chemistry lies not in hardware or software alone, but in their coordinated evolution—a lesson that extends beyond chemistry to computational science as a whole.

Proving the Model: Validation, Benchmarking, and Impact on Discovery

The field of computational chemistry has undergone a profound transformation, evolving from a supplementary tool into a core driver of scientific discovery. This evolution has been fueled by a continuous cycle of validation, where computational predictions inform experimental design, and experimental results, in turn, refine and validate the computational models. This iterative process has established a powerful feedback loop, accelerating the pace of research and increasing the reliability of scientific outcomes. The exploration of chemical space—the vast universe of all possible chemical compounds—exemplifies this synergy. Historically, this exploration was driven by experimental synthesis, but it is now increasingly guided by computational prediction, creating a more efficient and targeted research paradigm [73]. This technical guide examines the historical development, methodologies, and practical applications of this validation cycle, providing researchers with the frameworks and tools necessary to implement robust validation protocols in their work.

Historical Expansion of the Chemical Space (1800–2015)

The systematic exploration of chemical space provides critical context for the development of computational chemistry. Analysis of millions of reactions stored in the Reaxys database reveals that the reported synthesis of new compounds grew exponentially from 1800 to 2015 at a stable annual rate of 4.4%, a trend remarkably resilient to major world events like the World Wars [4]. This exploration has unfolded through three distinct historical regimes, each characterized by different growth patterns and variability in annual compound output.

Table 1: Historical Regimes in Chemical Exploration (1800-2015)

Regime	Period	Annual Growth Rate (μ)	Standard Variation (σ)	Key Characteristics
Proto-organic	Before 1861	4.04%	0.4984	High variability; mix of extraction and early synthesis; dominated by C, H, N, O, and halogen-based compounds [4].
Organic	1861–1980	4.57%	0.1251	Lower variability guided by structural theory; synthesis became the established method for reporting new compounds [4].
Organometallic	1981–2015	2.96%	0.0450	Smallest variability; rise of organometallic compounds; period further split into sub-regimes with differing growth [4].

A detailed analysis of these regimes shows that the transition between them was sharp, indicating significant shifts in chemical practice rather than a gradual evolution [4]. The Proto-organic regime was marked by uncertain year-to-year output and a high percentage of metal compounds, though carbon-hydrogen compounds consistently dominated. The Organic regime, initiated around the advent of structural theory, saw a century of more regular and guided production. The current Organometallic regime is the most regular, though its overall growth rate is lower, potentially reflecting the increasing complexity of synthesizing novel compounds and a greater reliance on computational guidance to navigate an increasingly vast chemical space [4] [73].

The Modern Validation Framework: Calibration and Sharpness

As computational methods became central to chemical research, the need for rigorous validation of their predictions, especially the associated uncertainties, became paramount. The Calibration-Sharpness (CS) framework, originally developed in meteorology, is now a principled framework for optimizing and validating uncertainty-aware methods, including machine learning models in computational chemistry [74].

• Calibration refers to the statistical consistency between predicted probabilities and observed frequencies. A well-calibrated model's predicted uncertainty intervals should match the actual error distribution (e.g., a 90% prediction interval should contain the true value 90% of the time).
• Sharpness refers to the concentration of the predictive distributions. Sharper predictions are more precise and therefore more informative, provided they are also well-calibrated.

The goal within the CS framework is to obtain predictions that are both sharp and well-calibrated [74]. The framework introduces the concept of tightness, which is a composite property ensuring that the uncertainty intervals are as narrow as possible (sharp) while still being statistically reliable (calibrated). Validation techniques within this framework range from elementary graphical checks (e.g., probability integral transform histograms) to more sophisticated analyses based on local calibration statistics [74].

Experimental Protocols for Validating Computational Predictions

Implementing the CS framework requires concrete methodological steps. The following protocol outlines the key stages for validating prediction uncertainties (PU) in computational chemistry, adaptable to various applications from quantum chemistry to quantitative structure-activity relationship (QSAR) modeling.

Protocol: Prediction Uncertainty Validation

1. Objective Definition

• Clearly define the chemical property or activity to be predicted.
• Establish the required level of uncertainty for the model's intended use (e.g., lead optimization vs. high-throughput virtual screening).

2. Data Curation and Partitioning

• Compile a high-quality dataset with reliable experimental measurements.
• Partition the data into training, validation, and test sets. The test set must be held out entirely until the final model evaluation to ensure an unbiased assessment.

3. Model Training and Uncertainty Quantification

• Train the computational model (e.g., a Gaussian process regression, a neural network with dropout, or an ensemble method) on the training set.
• Configure the model to output both a predicted value and an associated uncertainty estimate for each data point.

4. Calibration-Sharpness Analysis

• Calculate Calibration Statistics: On the validation set, compare the predicted uncertainties to the actual observed errors. This can be done by grouping predictions into bins based on their predicted uncertainty and checking if the observed variance within each bin matches the predicted variance [74].
• Generate Diagnostic Plots: Create visualizations such as calibration plots (observed frequency vs. predicted probability) and sharpness diagrams [74].
• Refine Model: If the model is poorly calibrated, apply calibration techniques such as isotonic regression or Platt scaling to adjust the output probabilities. Re-iterate until satisfactory performance is achieved on the validation set.

5. Final Validation and Tightness Assessment

• Apply the finalized model to the pristine test set.
• Evaluate the model's calibration and sharpness on this set to obtain an unbiased performance estimate.
• Assess the overall tightness of the predictions, ensuring the uncertainty intervals are both reliable and informative [74].

Visualizing the Validation Workflow

The following diagram illustrates the iterative, cyclical nature of the validation process, integrating both computational and experimental elements.

Case Study: Validating Chemical Probes for Drug Discovery

The NIH's Molecular Libraries Program produced hundreds of chemical probes through high-throughput screening (HTS), presenting a prime opportunity to apply computational validation. A study was conducted to determine if computational models could predict the evaluations of an expert medicinal chemist who assessed over 300 NIH probes for chemistry quality [75].

Experimental Protocol:

• Expert Evaluation: A medicinal chemist with over 40 years of experience scored each probe as "desirable" or "undesirable" based on criteria including excessive literature references (potential lack of selectivity), zero literature references (uncertain biological quality), and predicted chemical reactivity (e.g., Pan-Assay Interference Compounds or PAINS) [75].
• Descriptor Calculation: Molecular properties (e.g., molecular weight, logP, pKa, heavy atom count, rotatable bonds) were calculated for each probe [75].
• Model Building: A process of sequential Bayesian model building and iterative testing was used to create a classifier that could learn from the expert's evaluations [75].
• Validation: The model's accuracy was tested against the human expert's classifications and compared to other computational filters like PAINS and QED (Quantitative Estimate of Drug-likeness) [75].

Findings: The analysis revealed that over 20% of the NIH probes were considered undesirable by the expert. The Bayesian model achieved accuracy comparable to other established drug-likeness measures, demonstrating that human expert due diligence can be computationally predicted and scaled to assist in the validation of chemical probes before significant resources are invested [75]. This creates a powerful pre-experimental validation step.

The Scientist's Toolkit: Key Research Reagents and Materials

The following table details essential computational and experimental "reagents" central to the validation cycle in computational chemistry and drug discovery.

Table 2: Key Research Reagent Solutions for Computational Validation

Tool/Reagent	Function/Explanation
Reaxys/Beilstein Database	A large repository of chemical reactions and compounds used for historical analysis, model training, and validation [4].
Bayesian Classification Models	Machine learning models used to predict the quality or desirability of compounds, learning from expert-labeled data [75].
PAINS Filters	A set of structural alerts used to identify compounds likely to be pan-assay interference compounds (false positives) in biological assays [75].
QED (Quantitative Estimate of Drug-likeness)	A computational metric that provides a quantitative score of a compound's overall drug-likeness based on its molecular properties [75].
Chemical Probes (e.g., from MLPCN)	Well-characterized small molecules used to modulate specific protein functions in experimental settings; the subject of validation studies [75].
CDD Vault / Collaborative Databases	Software platforms that facilitate the management, analysis, and sharing of chemical and biological data, enabling collaborative validation [75].

The journey from the proto-organic chemistry of the 19th century to the modern, computation-driven discipline illustrates a fundamental shift in scientific practice. The exponential growth of chemical space has necessitated a more intelligent, predictive approach to exploration. The cycle of validation, underpinned by frameworks like Calibration-Sharpness and enabled by computational tools that can emulate expert judgment, has refined experimental science by making it more efficient, reliable, and insightful. As computational models continue to evolve, this synergistic cycle will only deepen, further blurring the lines between prediction and experiment and opening new frontiers in our understanding and manipulation of the molecular world.

The evolution of computational chemistry from the 19th century to the present represents one of the most significant transformations in scientific methodology. From early theoretical foundations to contemporary high-throughput virtual screening, computational approaches have become indispensable partners to experimental science. This progression necessitates rigorous benchmarking frameworks to evaluate the predictive accuracy of computational methods against experimental data. As computational techniques grow increasingly integral to fields like drug discovery, where even minute errors of 1 kcal/mol in binding affinity predictions can lead to erroneous conclusions, the importance of robust validation cannot be overstated [76].

The historical development of computational chemistry reveals a discipline shaped by exponential growth in chemical knowledge. Analysis of chemical databases shows that the reporting of new compounds has followed an exponential growth pattern from 1800 to 2015 with a stable 4.4% annual growth rate, persisting through world wars and theoretical revolutions [4]. This expansion has occurred through three distinct historical regimes: a proto-organic period (pre-1861) characterized by high variability in annual compound output, an organic regime (1861-1980) with more regular production guided by structural theory, and the current organometallic regime (post-1981) featuring the most stable output patterns [4]. Within this historical context, benchmarking provides the critical framework for validating computational methods against experimental reality throughout chemistry's development.

Historical Development of Computational Chemistry

Foundational Period (1927-1970)

The origins of computational quantum chemistry trace to the pioneering work of Walter Heitler and Fritz London, who performed the first theoretical chemistry calculations using valence bond theory in 1927 [3]. This foundational period was characterized by the development of quantum mechanical theories and their initial application to chemical systems, documented in influential texts such as Pauling and Wilson's "Introduction to Quantum Mechanics with Applications to Chemistry" (1935) and Coulson's "Valence" (1952) [3].

The advent of efficient computer technology in the 1940s enabled practical solutions to complex wave equations for atomic systems. A pivotal advancement came with Clemens C. J. Roothaan's 1951 paper on the Linear Combination of Atomic Orbitals Molecular Orbitals (LCAO MO) approach, which became one of the most cited papers in the Reviews of Modern Physics [3]. The first ab initio Hartree-Fock calculations on diatomic molecules were performed at MIT in 1956 using Slater orbitals, while the first polyatomic calculations employing Gaussian orbitals were conducted in the late 1950s by Boys and coworkers [3].

Methodological Diversification (1970-1990)

The 1970s witnessed the emergence of computational chemistry as a distinct discipline, marked by the development of diverse methodological approaches. Efficient ab initio computer programs including ATMOL, Gaussian, IBMOL, and POLYAYTOM accelerated calculations of molecular orbitals during this period [3]. Simultaneously, molecular mechanics methods such as the MM2 force field were developed, primarily by Norman Allinger [3]. The term "computational chemistry" first appeared in the 1970 book "Computers and Their Role in the Physical Sciences" by Fernbach and Taub, and the field gained formal recognition with the launch of the Journal of Computational Chemistry in 1980 [3].

Modern Integration (1990-Present)

The contemporary era has seen computational chemistry fully integrated into scientific research and recognized through highest academic honors. The 1998 Nobel Prize in Chemistry awarded to Walter Kohn for density-functional theory and John Pople for development of computational methods in quantum chemistry signaled the field's maturity [3]. This was followed by the 2013 Nobel Prize to Martin Karplus, Michael Levitt, and Arieh Warshel for developing multiscale models for complex chemical systems [3].

Current computational chemistry encompasses multiple specialized fields including molecular structure prediction, chemical database management, quantitative structure-property relationships (QSPR), synthesis planning, and drug design [3]. The field now leverages exponentially growing computing resources alongside vast virtual libraries containing billions of drug-like small molecules, enabling unprecedented capabilities in ligand screening and drug discovery [52].

Table 1: Historical Regimes in Chemical Exploration (1800-2015)

Regime Period	Annual Growth Rate	Key Characteristics	Primary Compound Types
Proto-organic (pre-1861)	4.04%	High variability in annual output; early synthesis development	Mixed organic/inorganic; rising C/H compounds
Organic (1861-1980)	4.57%	Regular production guided by structural theory	Carbon-based organic compounds dominate
Organometallic (1981-2015)	2.96%	Most stable output; computational guidance	Organometallic complexes; diverse compositions

Contemporary Benchmarking Frameworks

Domain-Specific Benchmark Development

The escalating complexity of computational methods has driven the creation of specialized benchmarks to evaluate performance on domain-specific tasks. In quantum science, QuantumBench represents the first comprehensive benchmark for evaluating large language models (LLMs) on quantum domain tasks [77]. This human-authored dataset comprises approximately 800 undergraduate-level multiple-choice questions across nine quantum science subfields, including quantum mechanics, quantum computation, quantum chemistry, quantum field theory, photonics, and nuclear physics [77]. The benchmark systematically examines how well models understand quantum phenomena and their sensitivity to variations in question format and wording.

For biomolecular interactions, the "QUantum Interacting Dimer" (QUID) framework establishes a "platinum standard" for benchmarking ligand-pocket interaction energies [76]. QUID contains 170 non-covalent molecular dimers modeling chemically and structurally diverse ligand-pocket motifs, with robust binding energies obtained through complementary Coupled Cluster (CC) and Quantum Monte Carlo (QMC) methods achieving exceptional agreement of 0.5 kcal/mol [76]. This framework specifically addresses the challenging nature of modeling non-covalent interactions in realistic binding environments.

Established Computational Databases

The National Institute of Standards and Technology (NIST) maintains the Computational Chemistry Comparison and Benchmark Database (CCCBDB), which provides reference data for validating computational methods against experimental measurements [78]. This resource enables researchers to assess the performance of various computational methods across diverse chemical systems.

Specialized databases have also emerged to support specific applications, particularly in drug discovery. Publicly available resources include:

• BindingDB: Experimental data on protein-small molecule interactions [3]
• RCSB Protein Data Bank: 3D structures of macromolecules and small molecules [3]
• ChEMBL: Data on drug discovery and assay results [3]
• DrugBank: Information on drug mechanisms and targets [3]

These databases provide essential reference data for benchmarking computational predictions against experimental observations across diverse chemical space.

Key Benchmarking Methodologies

Binding Affinity Prediction Methods

Accurately predicting binding free energies (ΔG_bind) represents a crucial benchmark for computational methods in drug design. The molecular mechanics energies combined with the Poisson-Boltzmann or generalized Born and surface area continuum solvation (MM/PBSA and MM/GBSA) methods have emerged as popular intermediate approaches between empirical scoring and strict alchemical perturbation methods [79]. These end-point methods estimate binding free energies using the formula:

ΔGbind = Gcomplex - (Greceptor + Gligand)

Where the free energy of each state is calculated as: G = EMM + Gsolvation - TS

EMM represents molecular mechanics energy from bonded, electrostatic, and van der Waals interactions; Gsolvation includes polar and non-polar solvation contributions; and the -TS term accounts for entropic effects [79].

Two primary approaches exist for ensemble averaging in MM/PBSA calculations: the three-average approach (3A-MM/PBSA) using separate simulations of complex, receptor, and ligand; and the more common one-average approach (1A-MM/PBSA) using only complex simulations with statistical separation of components [79]. While 1A-MM/PBSA offers improved precision and computational efficiency, it may overlook conformational changes upon binding.

Quantum Mechanical Benchmarking

For highest-accuracy predictions, quantum mechanical methods provide essential benchmarking capabilities. The QUID framework employs complementary "gold standard" methods—Coupled Cluster theory and Fixed-Node Diffusion Monte Carlo—to establish reference interaction energies for ligand-pocket systems [76]. This approach achieves exceptional agreement of 0.5 kcal/mol, providing a robust benchmark for evaluating more approximate methods.

Density functional theory (DFT) methods with dispersion corrections have demonstrated promising performance in QUID benchmarks, with several functionals providing accurate energy predictions despite variations in calculated van der Waals forces [76]. In contrast, semiempirical methods and empirical force fields require significant improvements in capturing non-covalent interactions, particularly for non-equilibrium geometries sampled during binding processes [76].

Table 2: Performance of Computational Methods in QUID Benchmarking [76]

Method Category	Typical Performance	Strengths	Limitations
Coupled Cluster/ QMC ("Platinum Standard")	0.5 kcal/mol agreement	Highest accuracy; robust reference	Computationally prohibitive for large systems
DFT with Dispersion	Variable (often < 1 kcal/mol)	Balanced accuracy/efficiency	Force orientation discrepancies
Semiempirical Methods	Requires improvement	Computational efficiency	Poor NCI description for non-equilibrium geometries
Empirical Force Fields	Requires improvement	High throughput	Limited transferability; approximate NCI treatment

Applications in Drug Discovery

Virtual Screening and Lead Optimization

Computational approaches have dramatically transformed the drug discovery pipeline, enabling rapid identification of potential drug candidates from ultralarge chemical spaces. Structure-based virtual screening of gigascale compound libraries has become increasingly feasible through advances in computational efficiency and method development [52]. These approaches demonstrate remarkable success, with examples including the identification of subnanomolar hits for GPCR targets through ultra-large docking and the discovery of clinical candidates after screening billions of compounds while synthesizing only dozens of molecules for experimental validation [52].

Iterative screening approaches combining deep learning predictions with molecular docking have further accelerated the exploration of chemical space [52]. For instance, the V-SYNTHES method enables efficient screening of over 11 billion compounds using a synthon-based approach, successfully validating performance on GPCR and kinase targets [52]. These computational advancements significantly democratize drug discovery by reducing the time and cost associated with traditional experimental approaches.

Free Energy Calculations

Binding affinity prediction through free energy calculations represents a critical application where benchmarking against experimental data is essential. MM/PBSA and related methods have been widely applied to protein-ligand systems, protein-protein interactions, and conformer stability assessment [79]. While these methods offer a balance between computational cost and accuracy, they contain several approximations that limit absolute accuracy, including treatment of conformational entropy and solvent effects [79].

More rigorous alchemical perturbation methods provide higher theoretical accuracy but require extensive sampling of physical and unphysical states, making them computationally intensive for routine application [79]. The development of improved benchmarks like QUID enables systematic evaluation of these methods across diverse chemical space, guiding method selection and development for specific applications [76].

Experimental Protocols

QUID Benchmark Implementation

The Quantum Interacting Dimer (QUID) benchmark provides a robust framework for evaluating computational methods on ligand-pocket interactions. The implementation protocol involves:

• System Selection: Nine large drug-like molecules (up to 50 atoms) from the Aquamarine dataset are selected as host monomers, representing diverse chemical compositions including C, N, O, H, F, P, S, and Cl atoms [76].

• Ligand Representation: Two small monomers (benzene and imidazole) represent common ligand motifs, capturing prevalent interaction types including aliphatic-aromatic, H-bonding, and π-stacking [76].

• Structure Generation: Initial dimer conformations are generated with aromatic rings aligned at 3.55±0.05 Å distance, followed by optimization at PBE0+MBD theory level [76].

• Classification: Equilibrium dimers are categorized as 'Linear', 'Semi-Folded', or 'Folded' based on large monomer geometry, representing different pocket packing densities [76].

• Non-Equilibrium Sampling: Sixteen representative dimers are used to generate non-equilibrium conformations along dissociation pathways using dimensionless factor q (0.90-2.00 relative to equilibrium distance) [76].

• Reference Calculations: Interaction energies are computed using complementary LNO-CCSD(T) and FN-DMC methods to establish robust reference values with minimal uncertainty [76].

MM/PBSA Binding Affinity Protocol

The MM/PBSA methodology for binding free energy estimation follows these key steps:

• System Preparation: Generate molecular structures of receptor, ligand, and complex using appropriate protonation states and initial coordinates [79].

• Molecular Dynamics Simulation: Perform explicit solvent molecular dynamics simulations to generate conformational ensembles:

  • For 1A-MM/PBSA: Simulate only the complex
  • For 3A-MM/PBSA: Simulate complex, receptor, and ligand separately [79]

• Trajectory Processing: Extract snapshots at regular intervals from production trajectories, removing solvent molecules for subsequent calculations [79].

• Energy Calculations: For each snapshot, compute:

  • Molecular mechanics energy (bonded, electrostatic, van der Waals)
  • Polar solvation energy using Poisson-Boltzmann or Generalized Born models
  • Non-polar solvation energy based on solvent-accessible surface area [79]

• Entropy Estimation: Calculate vibrational entropy through normal-mode analysis (computationally intensive) or approximate methods [79].

• Free Energy Calculation: Combine energy components according to: ΔGbind = ⟨Gcomplex⟩ - ⟨Greceptor⟩ - ⟨Gligand⟩ where G = EMM + Gsolvation - TS [79]

• Statistical Analysis: Compute mean and standard error across snapshots to determine binding affinity estimates and precision [79].

The Scientist's Toolkit

Table 3: Essential Computational Chemistry Software and Databases

Resource	Type	Primary Function	Application in Benchmarking
NWChem [80]	Quantum Chemistry Software	Ab initio calculations on biomolecules, nanostructures, and solids	High-performance computational chemistry calculations
Gaussian [3]	Electronic Structure Program	Ab initio, DFT, and semiempirical calculations	Molecular orbital calculations; method development
CCCBDB [78]	Benchmark Database	Experimental and computational reference data	Validation of computational methods
Reaxys [4]	Chemical Database	Millions of reactions and compounds	Historical chemical data analysis
BindingDB [3]	Bioactivity Database	Protein-ligand interaction data	Validation of binding affinity predictions

Methodological Approaches

Table 4: Computational Methods for Binding Affinity Prediction

Method	Theoretical Basis	Accuracy/Effort Trade-off	Best Applications
Docking/Scoring [79]	Empirical scoring functions	Fast but limited accuracy	Initial screening; binding mode prediction
MM/PBSA/GBSA [79]	Molecular mechanics with implicit solvation	Intermediate accuracy/effort	Binding affinity trends; system prioritization
Alchemical Perturbation [79]	Statistical mechanics	High accuracy but intensive	Relative binding affinities of similar compounds
DFT with Dispersion [76]	Quantum mechanics with dispersion corrections	High accuracy for NCIs	Non-covalent interaction analysis
Coupled Cluster/QMC [76]	Highest-level quantum mechanics	Benchmark accuracy; prohibitive for large systems	Reference values; method validation

The benchmarking of computational methods against experimental data represents a cornerstone of modern computational chemistry, enabling the validation and refinement of theoretical approaches against empirical reality. As computational methodologies continue to evolve alongside exponential growth in chemical knowledge, robust benchmarking frameworks like QuantumBench and QUID provide essential validation for applying these methods to scientific challenges.

The historical development of computational chemistry reveals a discipline that has progressively increased its capability to predict and rationalize chemical phenomena, with benchmarking serving as the critical link between computation and experiment. As the field advances toward increasingly complex problems in drug discovery, materials design, and beyond, continued development of comprehensive benchmarks will ensure that computational methods provide reliable guidance for scientific exploration and technological innovation.

In the context of drug discovery, where computational approaches now enable the screening of billions of compounds, rigorous benchmarking provides the foundation for trusting computational predictions enough to guide experimental investment. The ongoing refinement of these benchmarks, particularly for challenging properties like binding affinities and non-covalent interactions, will further accelerate the productive integration of computation and experimentation across chemical sciences.

The evolution of chemistry from the 19th century to the present day is inextricably linked to the development of systems for organizing and retrieving chemical information. The field of cheminformatics, though formally named only in the late 1990s, has roots extending back to the mid-20th century with pioneering work on machine-readable chemical structures and substructure searching algorithms [81]. This established the foundation for the Similar Property Principle—that structurally similar molecules often have similar properties—which became a cornerstone for chemical database design [81].

The late 20th and early 21st centuries witnessed an explosion of chemical data, driven by automated synthesis and high-throughput screening. This necessitated the creation of large-scale, curated databases, moving beyond simple literature compilations to sophisticated systems enabling complex queries based on chemical structures, properties, and bioactivities. In this landscape, Reaxys and ChEMBL emerged as premier resources, each with distinct strengths and histories. Their development reflects the broader trajectory of computational chemistry, shifting from manual data collection to integrated, algorithm-driven discovery platforms essential for modern research disciplines like Quantitative Structure-Activity Relationship (QSAR) modeling [82].

The Evolution of Major Chemical Databases

The Pre-History and Foundations (Pre-2000)

The technological underpinnings of modern chemical databases were laid decades before their graphical user interfaces came into existence. Early systems in the 1950s and 60s recognized that chemical structures could be represented as labeled graphs, and thus substructure searching could be implemented via subgraph isomorphism algorithms [81]. A pivotal moment was the development of the Morgan algorithm at Chemical Abstracts Service (CAS) to generate unique molecular identifiers, a technique that remains influential in graph-based chemical processing [81].

As chemical structure files grew, efficient searching required pre-filtering methods. The 1970s saw the development of screening systems that used binary-vector fingerprints to encode substructural fragments, drastically reducing the number of structures that required the computationally expensive subgraph isomorphism search [81]. The 1980s brought forth similarity searching methods, which quantified molecular resemblance using the same fragment sets developed for substructure search screening, thereby enabling effective virtual screening based on the Similar Property Principle [81]. These foundational advances in graph theory, indexing, and similarity searching provided the essential toolkit upon which Reaxys, ChEMBL, and their contemporaries were built.

The Modern Database Landscape

Today's chemical database ecosystem is composed of several major platforms, each with a unique profile of content sources, size, and primary use cases. The table below summarizes the key characteristics of the most prominent resources.

Table 1: Key Characteristics of Major Chemical Databases

Database	Primary Content & Focus	Key Historical Sources	Notable Features
Reaxys [83]	Organic, inorganic, and organometallic compounds and reactions; extracted from patent and journal literature.	Beilstein Handbook (literature from 1771), Gmelin (inorganic/organometallic), Patent Chemistry Database.	Intuitive interface for reaction retrieval, synthesis planning, and property searching. Integrated commercial compound sourcing (Reaxys Commercial Substances).
ChEMBL [84]	Manually curated bioactive molecules with drug-like properties; bioactivity data (binding, functional assays, ADMET).	European Bioinformatics Institute (EBI); data extracted from medicinal chemistry literature.	Detailed bioactivity data (targets, assays, pharmacokinetics). Directly supports drug discovery and lead optimization.
PubChem [85]	Aggregated bioactivity data from high-throughput screens and scientific contributors; broad substance repository.	Launched by NIH (2004). Sources include research groups and commercial compound vendors.	Massive scale (95M+ compounds). Direct link to biological assay data and biomedical literature via NCBI.
ChemSpider [85] [84]	Chemical structure database aggregating hundreds of data sources.	Developed by the Royal Society of Chemistry; acquired in 2009.	Community-curated structure database. Provides fast text and structure search across 35M+ structures.
CAS (Chemical Abstracts Service)	The most comprehensive curated source of chemical substance information.	Founded in 1907. The CAS Registry System was a pioneer in chemical database creation [81].	The largest (134M+ substances) and most authoritative database of disclosed chemical substances.

The relationships and data flow between these resources, as well as their integration into the research workflow, can be visualized in the following diagram.

Database Ecosystem and Research Workflow

Reaxys and ChEMBL: A Comparative Technical Guide

Reaxys: A Deep Dive into Content and Functionality

Reaxys represents the modern digital evolution of two legendary chemical handbooks: Beilstein (for organic chemistry) and Gmelin (for inorganic and organometallic chemistry). Its core strength lies in the deep, expert curation of data extracted from the chemical literature and patents, encompassing compounds, reactions, and physicochemical properties [83].

Key Integrated Databases within Reaxys:

• Target and Bioactivity: Focuses on the intersection of small molecules and bioactivity, providing detailed data on affinity, potency, specificity, pharmacokinetics, and toxicity to support drug discovery and lead optimization [83].
• Reaxys Commercial Substances (RCS): Integrates a growing pool of over 250 chemical vendors, containing over 165 million substances with associated product details like price, purity, and availability, facilitating synthesis-or-purchase decisions [83].
• PubChem Integration: Reaxys hosts PubChem content within its secure environment, allowing structure searches to be run seamlessly across all integrated databases simultaneously without impacting search performance [83].

Table 2: Reaxys Data Content and Historical Sources

Data Category	Specific Data Types	Historical Source/Origin
Substance Data	Melting/Boiling Point, Density, Refractive Index, Spectral Data, Solubility, Biological Activity.	Beilstein (organic compounds from 1771), Gmelin (inorganic/organometallic).
Reaction Data	Reactants, Products, Reagents, Solvents, Yield, Reaction Conditions.	Extracted from patents and journal literature.
Bibliographic Data	Citation, Patent Information, Experimental Procedures.	Cross-referenced from original sources.

ChEMBL: A Specialist Resource for Bioactive Molecules

ChEMBL, maintained by the European Bioinformatics Institute, is a manually curated database explicitly designed for drug discovery and medicinal chemistry. Its mission is to "facilitate the development of 'smarter leads'" by providing high-quality, detailed data on the biological activities of small molecules, extracted laboriously from the primary literature [83].

Core Data Content in ChEMBL:

• Chemical Entities: Over 2 million drug-like molecules with standardized structures and annotations.
• Bioactivities: More than 15 million data points from binding, functional, and ADMET (Absorption, Distribution, Metabolism, Excretion, Toxicity) assays.
• Target Information: Detailed information on protein targets, cell lines, and organisms, linking chemicals to their biological mechanisms.

Comparative Analysis for Research Applications

The choice between Reaxys and ChEMBL depends heavily on the research question. The table below provides a guide for selection based on common use cases in computational chemistry and drug development.

Table 3: Reaxys vs. ChEMBL: Application in Research Workflows

Research Task	Reaxys Application	ChEMBL Application
Compound/Reaction Validation	High. Validate reported synthetic pathways and physicochemical properties for novel compounds.	Limited. Focus is on biological activity, not synthesis.
Lead Compound Identification	Moderate. Identify structurally similar compounds with known synthesis.	High. Find compounds with confirmed activity against a specific biological target.
SAR/QSAR Modeling	Broad. Models based on diverse physicochemical properties.	Targeted. Models based on bioactivity data (IC50, Ki, etc.) against specific targets.
Synthesis Planning	High. Access to millions of verified reaction procedures.	Not a primary function.
Target Profiling	Limited.	High. Investigate a compound's activity profile across multiple biological targets.
Data Source	Patent literature, major chemistry journals.	Medicinal chemistry literature, focused on lead optimization studies.

Practical Application in QSAR Modeling

The QSAR Paradigm and Database Integration

Quantitative Structure-Activity Relationship (QSAR) modeling is a computational approach that establishes empirical relationships between chemical descriptors derived from molecular structure and experimentally measured properties or bioactivities [82]. The core workflow involves dataset compilation, chemical descriptor calculation, model construction using statistical or machine learning methods, and rigorous validation [82]. The rise of large-scale chemical databases has dramatically accelerated this process by providing the curated, high-quality data essential for building robust models.

Integrated Protocol for Database-Driven QSAR

This protocol outlines a robust methodology for constructing a QSAR model using data extracted and validated from Reaxys and ChEMBL.

Step 1: Objective Definition and Dataset Curation

• Define Endpoint: Clearly specify the biological or physicochemical property to be modeled (e.g., IC₅₀ for a specific enzyme, solubility, logP).
• Compound Acquisition (ChEMBL): Use the ChEMBL interface to search for compounds with the desired bioactivity endpoint. Employ filters for target (e.g., "Homo sapiens"), assay type (e.g., "Binding"), and data confidence. Export the resulting list of compounds and their bioactivity data.
• Data Augmentation (Reaxys): For compounds from ChEMBL (or a novel internal set), query Reaxys using the compound structures or names to retrieve supplementary physicochemical data (e.g., logP, molecular weight, melting point) and verify synthetic accessibility.

Step 2: Data Preparation and Curation

• Standardization: Standardize all chemical structures using a consistent toolkit (e.g., RDKit, OpenBabel) to normalize valencies, remove counterions, and generate canonical tautomers.
• Descriptor Calculation: Compute a suite of chemical descriptors for each standardized compound. These can include:
  • 1D Descriptors: Molecular weight, atom counts, logP.
  • 2D Descriptors: Topological indices, fragment counts, connectivity fingerprints.
  • 3D Descriptors: (Requires geometry optimization) Molecular surface area, volume, dipole moment.
• Dataset Division: Split the curated dataset into training and test sets using a rational method (e.g., Kennard-Stone, random sampling) to ensure the test set is representative of the chemical space covered by the training set.

Step 3: Model Building and Validation

• Algorithm Selection: Apply one or more machine learning algorithms to the training set. Common choices include:
  • Partial Least Squares (PLS)
  • Random Forest (RF)
  • Support Vector Machines (SVM)
  • Neural Networks (NN)
• Internal Validation: Assess model performance on the training set using cross-validation (e.g., 5-fold or 10-fold) and report metrics like Q² (cross-validated R²) and Root Mean Square Error of Cross-Validation (RMSECV).
• External Validation: Use the held-out test set for final model evaluation. Report standard metrics: R² (coefficient of determination), RMSE (Root Mean Square Error), and Mean Absolute Error (MAE).

Step 4: Model Application and Reporting

• Interpretation: Analyze the model to identify key structural features contributing to the activity (e.g., via variable importance plots from Random Forest).
• Prediction: Use the validated model to predict the activity of new, untested compounds from an in-house library or virtual combinatorial library.
• Reporting: Document the entire process following QSAR best practices, including the principles of the OECD Guidelines for QSAR Validation, ensuring transparency, reproducibility, and a defined domain of applicability [82].

The overall workflow, integrating both databases, is depicted below.

Integrated QSAR Workflow Using Reaxys and ChEMBL

Table 4: Essential Tools for Database-Driven QSAR Research

Tool/Resource	Type	Primary Function in QSAR	Access
Reaxys [83]	Commercial Database	Retrieving validated compound structures, properties, and synthetic pathways for dataset curation and validation.	Subscription
ChEMBL [84] [83]	Public Database	Sourcing high-quality, curated bioactivity data for model endpoints.	Free
RDKit	Cheminformatics Library	Chemical structure standardization, descriptor calculation, and fingerprint generation.	Open Source
KNIME / Python (scikit-learn)	Analytics Platform / Programming Language	Data preprocessing, machine learning model construction, and validation.	Open Source / Free
OECD QSAR Toolbox	Software Application	Identifying and filling data gaps, profiling chemical analogues, and applying OECD validation principles.	Free

The historical development of chemical databases, from punched-card systems to integrated platforms like Reaxys and ChEMBL, has fundamentally transformed the practice of computational chemistry. These resources have moved from being passive repositories to active engines of discovery, directly enabling the rigorous application of QSAR modeling. By providing access to meticulously curated and validated chemical and biological data, they allow researchers to build more predictive, reliable, and interpretative models. The continued evolution of these databases, particularly through the integration of artificial intelligence and machine learning for data extraction and prediction, promises to further accelerate drug discovery and materials design, solidifying their role as indispensable tools in the chemist's arsenal for the foreseeable future.

The field of chemistry is characterized by its relentless production of new substances and the innovative methods developed to procure them. Central to this enterprise is the concept of chemical space, a theoretical framework for organizing molecular diversity by postulating that different molecules occupy different regions of a mathematical space where the position of each molecule is defined by its properties [86]. This conceptualization has evolved significantly, particularly with the advent of computational chemistry, which provides the tools to navigate, quantify, and understand this vast space.

Chemical space is not merely a static collection of known compounds; it encompasses the near-infinite number of substances that could theoretically exist. The "size" of this space is staggering, with estimates for small organic molecules alone exceeding 10^60 compounds [86]. The exponential growth in the number of documented compounds, driven largely by organic synthesis, has been a defining feature of chemical expansion since the 19th century. Quantitative analysis reveals that the chemical space has been expanding at an exponential rate, doubling its known substances approximately every 16 years [87].

This whitepaper examines the quantitative expansion of chemical space within the context of computational chemistry's historical development from 1800 to 2015. We analyze the methodologies for quantifying chemical diversity, present key data on growth trends, detail experimental protocols for chemical space analysis, and visualize the conceptual and methodological frameworks that have enabled researchers to map this extraordinary terrain.

Historical Context: The Evolution of Chemical Knowledge and Computation

The period from 1800 witnessed foundational developments that progressively enabled the conceptualization and quantification of chemical space. Table 1 outlines key milestones that laid the groundwork for modern computational approaches to chemical space analysis.

Table 1: Key Historical Developments in Chemistry and Computation (1800-2015)

Time Period	Key Development	Contributors	Impact on Chemical Space
Early 1800s	Atomic Theory, Early Synthesis	John Dalton, Jöns Jakob Berzelius	Established particulate nature of matter and systematic composition [88].
1828	Synthesis of Urea	Friedrich Wöhler	Bridged organic/inorganic divide, expanding perceived boundaries of chemical space [88].
1860s-1870s	Periodic Table	Dmitri Mendeleev, Lothar Meyer	Provided a systematic framework for organizing elements, the building blocks of chemical space [8].
1927	First Quantum Chemical Calculations	Walter Heitler, Fritz London	Enabled first-principles prediction of molecular structure and properties from physics [3].
1950s-1960s	Early Digital Computers & Algorithms	Clemens C. J. Roothaan, Boys et al.	Made practical ab initio calculations on small molecules possible [3].
1970s	Rise of Semi-Empirical Methods & QSAR	Norman Allinger (MM2), Various	Allowed application to larger molecules; introduced similarity-based navigation of chemical space [3] [87].
1980s-1990s	Density Functional Theory, Large Databases	Walter Kohn, John Pople, Database Curators	Balanced accuracy and cost for complex systems; digitized chemical knowledge [3] [87].
2000s-Present	Cheminformatics, Big Data, Machine Learning	Various	Enabled analysis of ultra-large libraries (10^9+ compounds) and predictive modeling of chemical space [86] [87].

The trajectory of computational chemistry is marked by the interplay between theoretical advances and growing computational power. The first theoretical calculations in chemistry using quantum mechanics were performed by Heitler and London in 1927 [3]. The advent of efficient digital computers in the 1950s enabled the first semi-empirical atomic orbital calculations, with seminal advancements like the development of the Linear Combination of Atomic Orbitals Molecular Orbitals (LCAO MO) approach by Roothaan [3] [89]. By the 1970s, widely different computational methods began to coalesce into the recognized discipline of computational chemistry, further solidified by the founding of the Journal of Computational Chemistry in 1980 [3]. The 1998 and 2013 Nobel Prizes in Chemistry, awarded for developments in quantum chemistry and multiscale models, respectively, underscored the field's critical importance [3].

Quantifying the Chemical Space: Data and Trends

The Scale of Chemical Space

The theoretical bounds of chemical space are almost incomprehensibly large. Analysis suggests that the physical universe, with an estimated 10^80 particles, is insufficient to store the information of the possible chemical space [87]. A more constrained estimate, considering known chemistry and stable compounds, still yields a "Weininger number" of approximately 10^180 possible substances [87]. This vast theoretical landscape contrasts with the known chemical space, which, while much smaller, has been expanding at a remarkable pace.

Exponential Growth in Compound Discovery

Empirical studies of historical chemical records reveal a clear exponential trend. Research analyzing the evolution of chemical libraries has shown that the number of reported substances has been doubling every 16 years [87]. This pattern is analogous to other exponential growth phenomena, where a quantity increases by a constant percentage of the whole in a constant time period [90] [91]. The formula for such growth is expressed as:

x(t) = x₀(1 + r)^t

where x(t) is the quantity at time t, x₀ is the initial quantity, and r is the growth rate per time period [90]. For chemical space, this growth has been primarily driven by the synthesis of organic compounds [87].

Table 2: Quantitative Analysis of Chemical Space Growth and Diversity

Metric	Value / Finding	Method / Basis	Source
Theoretical Size	>10^60 (small organic molecules); ~10^180 (Weininger number)	Combinatorial analysis of possible atomic ensembles and molecular graphs.	[86] [87]
Historical Growth Rate	Doubling of known substances every ~16 years.	Analysis of digitized historical records of chemical reports over centuries.	[87]
Public Domain Compounds	~20 million bioactivity measurements, ~2.4 million compounds (ChEMBL).	Manual curation and data deposition from literature and patents.	[86]
Diversity vs. Size	Increasing the number of molecules does not automatically increase chemical diversity.	iSIM framework and BitBIRCH clustering analysis of library releases over time.	[86]
Modern Library Scale	Large (10^7 compounds) and ultra-large (10^9 compounds) libraries.	Virtual screening and combinatorial chemistry.	[86]

A critical insight from recent studies is that the mere increase in the number of compounds does not directly translate to an increase in chemical diversity. Analysis of public repositories like ChEMBL and PubChem using advanced cheminformatics tools shows that while the cardinality of the explored chemical space is growing, diversity—measured by molecular fingerprints and clustering—does not necessarily keep pace [86]. This highlights the necessity for rational quantification and guidance in the expansion of chemical libraries.

Methodologies for Analyzing Chemical Space

Navigating and quantifying the immense and growing chemical space requires specialized computational tools. The methodologies below represent the state-of-the-art in measuring the intrinsic diversity and evolutionary dynamics of compound libraries.

The iSIM Framework for Intrinsic Similarity

Objective: To efficiently calculate the average pairwise similarity (or diversity) within a very large library of compounds, bypassing the computationally infeasible O(N²) scaling of traditional methods.

Principle: The iSIM (intrinsic Similarity) method avoids explicit pairwise comparisons by analyzing the molecular fingerprints of all molecules in a library simultaneously. It operates in O(N) time, making it suitable for massive datasets [86].

Experimental Protocol:

• Molecular Representation: Represent each molecule in the library using a binary molecular fingerprint (e.g., ECFP, Morgan fingerprint). Each fingerprint is a vector of bits (length M), where a '1' indicates the presence of a specific structural feature.
• Fingerprint Matrix Construction: Arrange all N fingerprint vectors into a matrix of size N × M.
• Column Summation: For each column i (where i = 1 to M) in the matrix, calculate the sum k_i, which is the number of molecules that have that particular bit set to '1'.
• Intrinsic Tanimoto (iT) Calculation: Calculate the average of all pairwise Tanimoto similarities using the column sums [86]: iT = Σ[k_i(k_i - 1)/2] / Σ{ [k_i(k_i - 1)/2] + [k_i(N - k_i)] } The iT value represents the library's internal similarity. A lower iT indicates a more diverse collection.

Complementary Similarity Analysis:

• Molecule Removal: Iteratively remove each molecule from the library.
• iT Recalculation: Recalculate the iT value for the remaining set. This new value is the complementary similarity for the removed molecule.
• Interpretation: A low complementary similarity indicates a molecule that is central or "medoid-like" to the library's chemical space. A high value indicates an "outlier" molecule on the periphery.
• Temporal Tracking: By performing this analysis on different chronological releases of a library (e.g., ChEMBL releases 1-33), researchers can identify which releases contributed most to diversity and which regions of the chemical space were expanded [86].

The BitBIRCH Clustering Algorithm

Objective: To efficiently cluster millions of compounds into groups of structurally similar molecules, providing a "granular" view of the chemical space's structure.

Principle: BitBIRCH is inspired by the BIRCH (Balanced Iterative Reducing and Clustering using Hierarchies) algorithm but is adapted for binary fingerprint data and the Tanimoto similarity metric. It uses a tree structure to minimize the number of direct comparisons needed, enabling the clustering of ultra-large libraries [86].

Experimental Protocol:

• Data Ingestion: Stream the binary fingerprint data of the molecular library into the algorithm.
• Clustering Feature (CF) Tree Building: a. The algorithm builds a CF Tree by incrementally reading fingerprint vectors. b. Each leaf node in the tree contains a number of subclusters, characterized by a Clustering Feature, which for binary data incorporates the number of points in the cluster and the linear sum of the fingerprints. c. New fingerprints are routed to the closest subcluster in a leaf node, based on Tanimoto distance, if it falls within a threshold. Otherwise, a new subcluster is created. d. The tree is kept balanced by dynamically rebuilding it when a specified node size is exceeded.
• Cluster Extraction: After the CF Tree is built, a final clustering pass is performed on the leaf nodes to generate the final clusters.
• Analysis: The resulting clusters can be tracked over time to observe the formation of new clusters (indicating exploration of novel chemical space) and the growth of existing ones (indicating exploitation of known regions) [86].

Assembly Theory for Quantifying Molecular Complexity

Objective: To quantify the molecular complexity and the degree of selection required to produce a given molecule or ensemble of molecules, providing a new metric to distinguish randomly formed molecules from those that are the product of evolutionary or designed processes.

Principle: Assembly Theory (AT) defines objects by their possible formation histories. It introduces an assembly index (a_i), which is the minimal number of steps required to construct the object from basic building blocks, recursively using previously constructed objects. In chemical systems, bonds are the elementary operations [92].

Experimental Protocol:

• Deconstruction: The molecule is broken down into its constituent atoms.
• Pathway Reconstruction: The shortest path to reassemble the molecule is determined. This involves sequentially adding bonds, where at each step, any motif (atom or combined structure) already generated on the path is available for reuse.
• Assembly Index Calculation: The number of steps in this shortest path is the molecule's assembly index. A molecule like carbon dioxide (O=C=O) has a low assembly index, while a complex natural product like taxol has a very high one.
• Combining with Copy Number: The assembly index alone cannot detect selection. However, finding many identical copies (high copy number) of a molecule with a high assembly index is a strong indicator of a selection process, as it is statistically unlikely for such complex objects to form abundantly by chance alone [92]. This combination is proposed as a signature of life or sophisticated synthetic design.

Visualization of Chemical Space Analysis

The following diagrams, generated using Graphviz DOT language, illustrate the core logical relationships and workflows in chemical space analysis.

Conceptual Framework of Chemical Space

Workflow for Chemical Diversity Analysis

Modern computational analysis of chemical space relies on a suite of software tools, algorithms, and databases. The following table details key resources used in the featured methodologies.

Table 3: Key Research Reagent Solutions for Chemical Space Analysis

Tool / Resource	Type	Primary Function	Application in Chemical Space Analysis
iSIM Framework	Algorithm	Efficiently calculates the average pairwise similarity within a massive compound library.	Quantifying the intrinsic diversity of a library in O(N) time, enabling analysis of ultra-large datasets [86].
BitBIRCH	Clustering Algorithm	Clusters millions of molecular fingerprints based on Tanimoto similarity.	Provides a granular view of chemical space by identifying densely populated regions and tracking cluster evolution [86].
Molecular Fingerprints (e.g., ECFP, Morgan)	Molecular Representation	Encodes molecular structure as a bit string for computational comparison.	Serves as the fundamental data representation for similarity search, diversity analysis, and machine learning models [86].
Assembly Theory	Theoretical & Analytical Framework	Quantifies the minimal number of steps to construct a molecule and combines this with copy number.	Provides a metric for molecular complexity and evidence of selection, useful for analyzing biosynthetic and synthetic pathways [92].
Public Chemical Databases (ChEMBL, PubChem)	Data Repository	Stores curated chemical structures, bioactivity data, and associated metadata.	Provides the raw, large-scale data on known chemicals essential for empirical analysis of chemical space growth and diversity [86] [3].
Density Functional Theory (DFT)	Computational Method	Approximates the electronic structure of molecules using electron density.	Used for accurate calculation of molecular properties that can be used as coordinates in property-based chemical spaces [3].

The quantification of chemical space reveals a field in a state of continuous and exponential expansion, a process profoundly enabled by the parallel development of computational chemistry. From the early theoretical foundations of quantum mechanics to the modern era of cheminformatics and big data, computational tools have evolved to not only keep pace with the explosion of chemical entities but to provide the conceptual frameworks necessary to understand it. The key insight that the growth in the number of compounds does not automatically equate to an increase in diversity underscores the need for sophisticated metrics and protocols, such as the iSIM framework and BitBIRCH clustering. As we move forward, the integration of these quantitative measures with emerging paradigms like Assembly Theory promises to further illuminate the complex interplay between synthesis, discovery, and selection that defines the ever-growing map of chemical space. This refined understanding is critical for directing future synthetic efforts and accelerating the discovery of novel functional molecules in fields like drug development and materials science.

Conclusion

The historical development of computational chemistry from 1800 to 2015 represents a paradigm shift in scientific inquiry, transforming chemistry from a purely laboratory-based science to a discipline powerfully augmented by virtual exploration. The journey, marked by foundational quantum theories, the advent of digital computers, and Nobel-recognized methodological breakthroughs, has firmly established computation as a pillar of modern research. For biomedical and clinical research, the implications are profound. The ability to accurately model drug-receptor interactions, predict ADMET properties, and design novel catalysts in silico has dramatically accelerated the pace of discovery and reduced development costs. Future directions point toward more integrated multiscale models that seamlessly traverse from quantum to macroscopic scales, the incorporation of artificial intelligence to navigate chemical space more intelligently, and the continued development of methods to simulate complex biological processes like protein folding and signal transduction with unprecedented fidelity. The computer is now irreplaceable, standing alongside the test tube as an essential tool for unlocking the next generation of therapeutics and materials.

References

• 1. Chemical revolution [https://en.wikipedia.org/wiki/Chemical_revolution]
• 2. Chemical Revolution - an overview [https://www.sciencedirect.com/topics/psychology/chemical-revolution]
• 3. Computational chemistry [https://en.wikipedia.org/wiki/Computational_chemistry]
• 4. Exploration of the chemical space and its three historical ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6600933/]
• 5. Chemists discovered new compounds at an exponential rate ... [https://cen.acs.org/synthesis/Chemists-discovered-new-compounds-exponential/97/i25]
• 6. 2.1: Historical Development of Atomic Theory [https://chem.libretexts.org/Bookshelves/Inorganic_Chemistry/Inorganic_Chemistry_(LibreTexts)/02%3A_Atomic_Structure/2.01%3A_Historical_Development_of_Atomic_Theory]
• 7. John Dalton - Atomic Theory, Chemistry, Physics [https://www.britannica.com/biography/John-Dalton/Atomic-theory]
• 8. Significant Milestones in Chemistry: A Timeline of ... [https://www.chemistryviews.org/significant-milestones-in-chemistry-a-timeline-of-influential-chemists/]
• 9. 6 Major Figures in the History of Theoretical and ... [https://gradarticles.smu.edu/advancing-the-field/6-major-figures-in-the-history-of-computational-and-theoretical-chemistry]
• 10. Schrödinger equation [https://en.wikipedia.org/wiki/Schr%C3%B6dinger_equation]
• 11. Erwin Schrodinger [https://chemed.chem.purdue.edu/genchem/history/schrodinger.html]
• 12. Quantum Chemistry: Understanding the Schrödinger Equation [https://rosemaryfrancis.medium.com/quantum-chemistry-understanding-the-schr%C3%B6dinger-equation-588a9ba0b14a]
• 13. Brief History of Electronic Structure Calculations in ... [http://www.fortunejournals.com/articles/brief-history-of-electronic-structure-calculations-in-computational-chemistry.html]
• 14. Computational chemistry applications - Schrödinger [https://www.schrodinger.com/life-science/learn/white-papers/computational-chemistry-applications/]
• 15. [2511.01132] Screening in the Heitler-London Model [https://arxiv.org/abs/2511.01132]
• 16. Screening in the Heitler-London Model: Revisiting ... [https://arxiv.org/html/2511.01132v1]
• 17. 1.10: The Chemical Bond [https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Quantum_Chemistry_(Blinder)/01%3A_Chapters/1.10%3A_The_Chemical_Bond]
• 18. A comprehensive list of theoretical approximations that are ... [https://chemistry.stackexchange.com/questions/59634/a-comprehensive-list-of-theoretical-approximations-that-are-used-in-computationa]
• 19. 2 the emergence of computational chemistry - Publications [https://nap.nationalacademies.org/read/4886/chapter/4]
• 20. Digital chemistry: navigating the confluence of computation ... [https://pubs.rsc.org/en/content/articlehtml/2024/dd/d4dd00130c]
• 21. A history of ab initio computational quantum chemistry [https://www.sciencedirect.com/science/article/pii/0898552988900140]
• 22. The path to computational quantum chemistry [https://www.sciencedirect.com/science/article/abs/pii/S0039368114000533]
• 23. Beyond computational difficulties: Survey of the two ... [https://www.sciencedirect.com/science/article/abs/pii/S1355219816301113]
• 24. Basis set (chemistry) [https://en.wikipedia.org/wiki/Basis_set_(chemistry)]
• 25. Computational Organic Chemistry - PubMed Central - NIH [https://pmc.ncbi.nlm.nih.gov/articles/PMC11087259/]
• 26. 2.9: Computational Chemistry [https://chem.libretexts.org/Workbench/CHEM_110B%3A_Physical_Chemistry_-_Properties_of_Atoms_and_Molecules/02%3A_Electronic_Structure/2.09%3A_Computational_Chemistry]
• 27. AI in computational chemistry through the lens of a decade ... [https://pubs.rsc.org/en/content/articlehtml/2024/cc/d4cc00010b]
• 28. Development of new auxiliary basis functions ... [https://pubs.rsc.org/en/content/articlelanding/2015/cp/c4cp04286g]
• 29. Thirty years of density functional theory in computational ... [https://www.osti.gov/pages/biblio/1510353]
• 30. A comprehensive analysis of the history of DFT based on the ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6873586/]
• 31. Molecular mechanics [https://en.wikipedia.org/wiki/Molecular_mechanics]
• 32. Force field (chemistry) [https://en.wikipedia.org/wiki/Force_field_(chemistry)]
• 33. Molecular Mechanics - PMC - PubMed Central - NIH [https://pmc.ncbi.nlm.nih.gov/articles/PMC4026342/]
• 34. Gaussian (software) [https://en.wikipedia.org/wiki/Gaussian_(software)]
• 35. Molecular Mechanics Methods [https://gaussian.com/mm/]
• 36. Molecular Mechanic - an overview | ScienceDirect Topics [https://www.sciencedirect.com/topics/chemistry/molecular-mechanic]
• 37. A computational perspective on the Nobel Prize [https://www.nature.com/articles/s43588-022-00325-x]
• 38. Nobel Prize in Chemistry 2013: Multiscale modelling [https://blogs.rsc.org/cp/2013/10/09/nobel-prize-in-chemistry-2013-multiscale-modelling/]
• 39. Press release: The 1998 Nobel Prize in Chemistry [https://www.nobelprize.org/prizes/chemistry/1998/press-release/]
• 40. Timeline: The continuing evolution of density functional ... [https://www.microsoft.com/en-us/research/articles/timeline-the-continuing-evolution-of-density-functional-theory/]
• 41. Walter Kohn [https://en.wikipedia.org/wiki/Walter_Kohn]
• 42. Applications of density functional theory in COVID-19 drug ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8695517/]
• 43. All Nobel Prizes in Chemistry - NobelPrize.org [https://www.nobelprize.org/prizes/lists/all-nobel-prizes-in-chemistry/all/]
• 44. The Nobel Prize in Chemistry 1998 - NobelPrize.org [https://www.nobelprize.org/prizes/chemistry/1998/summary/]
• 45. Theoretical Frameworks for Multiscale Modeling and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4040314/]
• 46. Cresset Discovery case studies [https://cresset-group.com/discovery/case-studies/]
• 47. Drug Design Org: drugdesign.org [https://drugdesign.org/]
• 48. Machine Learning in Computational Surface Science and ... [https://www.frontiersin.org/journals/chemistry/articles/10.3389/fchem.2020.601029/full]
• 49. Materials science | Nature Computational ... [https://www.nature.com/subjects/materials-science/natcomputsci]
• 50. Using Quantum Simulations to Unlock the Secrets of ... [https://www.alcf.anl.gov/science/case-studies/using-quantum-simulations-unlock-secrets-molecular-science-gamess]
• 51. Computational Materials Science | Journal [https://www.sciencedirect.com/journal/computational-materials-science]
• 52. Computational approaches streamlining drug discovery [https://www.nature.com/articles/s41586-023-05905-z]
• 53. Application-specific Machine-Learned Interatomic ... [https://arxiv.org/abs/2506.05646]
• 54. Past, Present, and Future Perspectives on Computer-Aided ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10180087/]
• 55. On the cost–accuracy trade-off in electrolytes [https://www.nature.com/articles/s43588-022-00366-2]
• 56. Electronic correlation [https://en.wikipedia.org/wiki/Electronic_correlation]
• 57. New computational chemistry techniques accelerate the ... [https://news.mit.edu/2025/new-computational-chemistry-techniques-accelerate-prediction-molecules-materials-0114]
• 58. 6.5: Various Approaches to Electron Correlation [https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Advanced_Theoretical_Chemistry_(Simons)/06%3A_Electronic_Structure/6.05%3A_Various_Approaches_to_Electron_Correlation]
• 59. Many Body Quantum Magic MBQM 2025 [https://phys.washington.edu/events/2025-08-18/many-body-quantum-magic-mbqm-2025]
• 60. Quantum Computing Industry Trends 2025: A Year of ... [https://www.spinquanta.com/news-detail/quantum-computing-industry-trends-2025-breakthrough-milestones-commercial-transition]
• 61. QM/MM [https://en.wikipedia.org/wiki/QM/MM]
• 62. Review on the QM/MM Methodologies and Their Application ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC9105939/]
• 63. Applications and Advances of QM/MM Methods in ... [https://www.sciencedirect.com/science/article/abs/pii/S1574140008000091]
• 64. Hybrid Quantum Mechanics / Molecular Mechanics (QM ... [https://www.cecam.org/workshop-details/hybrid-quantum-mechanics-molecular-mechanics-qmmm-approaches-to-biochemistry-and-beyond-1030]
• 65. Software Development for Computational Chemistry - NCBI [https://www.ncbi.nlm.nih.gov/books/NBK44979/]
• 66. Evolving with the Computational Chemistry Landscape [https://pubmed.ncbi.nlm.nih.gov/33788546/]
• 67. Supercomputer [https://en.wikipedia.org/wiki/Supercomputer]
• 68. Quantum Advantage in Computational Chemistry? † [https://arxiv.org/html/2508.20972v1]
• 69. Software-Hardware Co-Optimization for Computational ... [https://arxiv.org/abs/2105.07127]
• 70. Welcome to the Era of Hardware-Algorithm Coevolution [https://kenkennedy.rice.edu/news/current-news/welcome-era-hardware-algorithm-coevolution]
• 71. Quantum algorithms for grid-based variational time evolution [https://quantum-journal.org/papers/q-2023-10-12-1139/?]
• 72. Methods [https://link.springer.com/chapter/10.1007/978-3-031-10094-9_6]
• 73. Chemical space: limits, evolution and modelling of an ... [https://www.sciencedirect.com/org/science/article/pii/S2635098X23000670]
• 74. Prediction uncertainty validation for computational chemists [https://arxiv.org/abs/2204.13477]
• 75. Computational Prediction and Validation of an Expert's ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4955571/]
• 76. Extending quantum-mechanical benchmark accuracy to ... [https://www.nature.com/articles/s41467-025-63587-9]
• 77. QuantumBench: A Benchmark for Quantum Problem Solving [https://arxiv.org/html/2511.00092v1]
• 78. NIST Computational and Chemistry ... Comparison Benchmark [https://catalog.data.gov/dataset/nist-computational-chemistry-comparison-and-benchmark-database-srd-101-e19c1]
• 79. The MM/PBSA and MM/GBSA methods to estimate ligand- ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4487606/]
• 80. NWChem [https://nwchemgit.github.io/index.html]
• 81. Searching chemical databases in the pre-history of ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11533634/]
• 82. QSAR without borders - PMC - PubMed Central - NIH [https://pmc.ncbi.nlm.nih.gov/articles/PMC8008490/]
• 83. Which databases are integrated in Reaxys? - Elsevier Support [https://www.elsevier.support/reaxys/answer/which-databases-are-integrated-in-reaxys]
• 84. List of useful databases | Chemistry Library [https://library.ch.cam.ac.uk/list-useful-databases]
• 85. Assessing Differences between Major Chemistry Databases [https://pmc.ncbi.nlm.nih.gov/articles/PMC5900829/]
• 86. Growth vs. Diversity: A Time-Evolution Analysis of the ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11870478/]
• 87. Chemical space: limits, evolution and modelling of an object ... [https://pubs.rsc.org/en/content/articlehtml/2022/dd/d2dd00030j]
• 88. Timeline of chemistry [https://en.wikipedia.org/wiki/Timeline_of_chemistry]
• 89. Historical development and scope of computational chemistry [https://fiveable.me/computational-chemistry/unit-1/historical-development-scope-computational-chemistry/study-guide/LZ17jq2QX2q6Dbpq]
• 90. Exponential growth [https://en.wikipedia.org/wiki/Exponential_growth]
• 91. Exponential Growth - an overview [https://www.sciencedirect.com/topics/engineering/exponential-growth]
• 92. Assembly theory explains and quantifies selection and ... [https://www.nature.com/articles/s41586-023-06600-9]