Mastering Overfitting and Underfitting: A Model-Informed Drug Development Perspective

Gabriel Morgan Dec 02, 2025 205

This article provides a comprehensive guide to overfitting and underfitting in machine learning, tailored for researchers and professionals in drug development.

Mastering Overfitting and Underfitting: A Model-Informed Drug Development Perspective

Abstract

This article provides a comprehensive guide to overfitting and underfitting in machine learning, tailored for researchers and professionals in drug development. It covers the foundational concepts of bias-variance tradeoff, explores methodological applications in MIDD, details advanced troubleshooting and optimization techniques for predictive models, and discusses robust validation frameworks. By aligning model complexity with specific Context of Use (COU), this resource aims to enhance the reliability and regulatory acceptance of AI/ML models in biomedical research, from early discovery to clinical decision support.

The Bias-Variance Tradeoff: Core Principles for Robust Model Generalization

Defining Overfitting and Underfitting in Machine Learning

Contents

In machine learning (ML), the ultimate goal is to develop models that generalize—they must perform reliably on new, unseen data after being trained on a finite dataset [1] [2]. The path to achieving this is fraught with two fundamental pitfalls: underfitting and overfitting. These concepts represent a critical trade-off between a model's simplicity and its complexity, directly impacting its predictive accuracy and utility in real-world applications, such as drug discovery and development [3]. For researchers and scientists, a deep understanding of these phenomena is not merely academic; it is essential for building robust, reliable, and interpretable models that can accelerate research and reduce failure rates in critical domains like healthcare. This guide provides an in-depth technical examination of overfitting and underfitting, framed within contemporary ML research.

Theoretical Foundations and Mathematical Framing

At its core, the challenge of model fitting is governed by the bias-variance trade-off, a fundamental concept that decomposes a model's generalization error into interpretable components [1] [4].

The Bias-Variance Decomposition

The expected prediction error on a new sample can be formally decomposed as follows: [ \text{Error} = \text{Bias}^2 + \text{Variance} + \text{Irreducible Error} ]

  • Bias: The error introduced by approximating a real-world problem, which may be exceedingly complex, with a simplified model. High bias causes the model to miss relevant relationships between features and the target output, leading to underfitting [1] [4].
  • Variance: The error introduced by the model's excessive sensitivity to small fluctuations in the training set. A high-variance model learns not only the underlying signal but also the noise in the training data, leading to overfitting [4] [5].
  • Irreducible Error: The inherent noise in the data that cannot be reduced by any model.

The following diagram illustrates the relationship between model complexity, error, the bias-variance tradeoff, and the resulting model behavior:

BiasVarianceTradeoff ModelComplexity Model Complexity Error Generalization Error ModelComplexity->Error Influences BiasVariance {Bias-Variance|{High Bias|High Variance}} Error->BiasVariance Decomposed into ModelBehavior {Model Behavior|{Underfitting|Overfitting}} BiasVariance->ModelBehavior Manifests as

Formal Definitions in the Empirical Risk Framework

Within the Empirical Risk Minimization (ERM) framework, overfitting and underfitting can be precisely defined [5]. Let ( h ) represent a prediction model from a hypothesis class ( H ), and ( l ) be a loss function.

  • Overfitting occurs when the empirical risk (training error) of model ( h ) is small relative to its true risk (test error). The model corresponds too closely to the training dataset and may fail to fit additional data reliably [2] [5].
  • Underfitting occurs when a model cannot achieve a sufficiently small empirical risk, indicating that it has failed to capture the underlying structure of the training data [2].
A Quantitative Comparison

The distinct characteristics of underfit, overfit, and well-generalized models are summarized in the table below for clear comparison. This is critical for rapid diagnosis during model development.

Table 1: Diagnostic Characteristics of Model Fit States

Feature Underfitting Overfitting Good Fit
Performance on Training Data Poor [1] [4] Excellent (often 95%+) [1] [6] Good [1]
Performance on Test/Validation Data Poor [1] [4] Poor [1] [4] Good [1]
Model Complexity Too Simple [1] Too Complex [1] Balanced [1]
Bias High [1] [4] Low [1] Low [1]
Variance Low [1] [4] High [1] Low [1]
Primary Fix Increase complexity/features [1] [4] Add more data/regularize [1] [4] Maintain current approach
Methodologies for Detection and Evaluation

Robust detection of overfitting and underfitting requires systematic validation protocols beyond a simple train-test split.

Key Detection Methods
  • Validation Set and Learning Curves: The most direct method is to monitor the model's performance on a held-out validation set during training. A signature of overfitting is a continuous decrease in training error while validation error begins to increase after a certain point. Underfitting is indicated when both training and validation error are high [1] [6].
  • K-Fold Cross-Validation: This technique involves splitting the data into 'k' subsets. The model is trained on k-1 folds and validated on the remaining fold, rotating the process for all folds. This provides a more reliable, robust estimate of model generalization performance and helps identify instability indicative of overfitting [1].
  • Nested Cross-Validation: For complex workflows involving feature selection and hyperparameter tuning, a nested protocol is essential. Feature selection and model fitting must be performed on the training fold of an outer cross-validation loop, with error estimation performed strictly on the held-out test fold. This prevents "data leakage" and optimistic bias in error estimates, a critical concern in high-dimensional data like genomics [2].

The following workflow diagram outlines a robust experimental protocol that incorporates these validation methods to mitigate overfitting and underfitting:

MLValidationWorkflow Start Full Dataset Split1 Stratified Split Start->Split1 TrainSet Training Set Split1->TrainSet TestSet Held-Out Test Set Split1->TestSet Locked until final evaluation Split2 K-Fold Cross-Validation TrainSet->Split2 FinalEval Evaluate on Held-Out Test Set TestSet->FinalEval CVTrain Training Fold (K-1) Split2->CVTrain CVVal Validation Fold (1) Split2->CVVal HyperTune Hyperparameter Tuning & Model Selection CVTrain->HyperTune CVVal->HyperTune Monitor for over/underfitting FinalTrain Train Final Model on Full Training Set HyperTune->FinalTrain FinalTrain->FinalEval Report Report Generalization Performance FinalEval->Report

Experimental Protocols and Empirical Evidence

Real-world case studies from recent literature highlight the practical implications and solutions for overfitting and underfitting.

Case Study 1: IoT Botnet Detection with a Multi-Model Framework

A 2025 study on IoT botnet detection provides a comprehensive framework for optimizing model fit [7].

  • Experimental Protocol: The researchers systematically addressed data quality across three distinct datasets (BOT-IOT, CICIOT2023, IOT23). Their methodology included a Quantile Uniform transformation to reduce feature skewness, a multi-layered feature selection process, and a robust model fitting optimization framework using Random Forest and Logistic Regression with threshold-based decision-making [7].
  • Findings on Model Fit: The study demonstrated significant performance variations across datasets. While BOT-IOT and CICIOT2023 allowed for high accuracy, IOT23 presented more complex, real-world challenges. The authors implemented cross-validation to reveal these dataset-specific fitting challenges, addressing class imbalance via SMOTE to prevent the model from underfitting to minority classes. Their final weighted soft-voting ensemble of Convolutional Neural Networks (CNN), Bidirectional Long Short-Term Memory (BiLSTM), Random Forest, and Logistic Regression achieved superior performance (100% accuracy on BOT-IOT, 99.2% on CICIOT2023, 91.5% on IOT23) by leveraging the strengths of individual models and mitigating their individual tendencies to overfit or underfit [7].
Case Study 2: Lung Cancer Level Classification with Traditional ML

A comprehensive analysis on lung cancer staging compared traditional ML models with deep learning [8].

  • Experimental Protocol: The research implemented a suite of models, including XGBoost (XGB), Logistic Regression (LR), and Random Forest (RF). A critical part of their methodology was the careful tuning of hyperparameters like learning rate and child weight to minimize the risk of overfitting [8].
  • Findings on Model Fit: The study concluded that traditional ML models, particularly XGBoost and Logistic Regression, outperformed more complex deep learning models, achieving nearly 100% classification accuracy. The authors argued that the deep learning models underperformed due to the limited dataset size, making them prone to overfitting. This underscores that model complexity must be appropriate for the available data volume. The success of well-regularized traditional models highlights an effective strategy to avoid overfitting while maintaining low bias in contexts with constrained data [8].

Table 2: Experimental Findings on Model Fit from Case Studies

Study Domain Key Methodology to Control Fit Finding on Over/Underfitting
IoT Botnet Detection (2025) [7] Cybersecurity Quantile Uniform transformation, multi-layered feature selection, ensemble learning Ensembles mitigated overfitting; complex datasets (IOT23) revealed harder generalization challenges.
Lung Cancer Classification [8] Medical Diagnostics Careful tuning of learning rate and child weight in XGBoost Traditional ML (XGB, LR) outperformed deep learning, which was prone to overfitting on limited data.
The Scientist's Toolkit: Research Reagent Solutions

The following table details key methodological "reagents" — techniques and tools — essential for designing experiments to diagnose and prevent fitting problems.

Table 3: Essential Research Reagents for Managing Model Fit

Research Reagent Function/Brief Explanation Primary Use Case
K-Fold Cross-Validation [1] Provides a robust estimate of generalization error by rotating data through k training and validation splits. Generalization Error Estimation
L1 (Lasso) & L2 (Ridge) Regularization [1] [3] Adds a penalty to the loss function to constrain model complexity. L1 can shrink coefficients to zero, performing feature selection. Preventing Overfitting
Dropout [1] [3] A regularization technique for neural networks where random neurons are ignored during training, preventing complex co-adaptations. Preventing Overfitting in DNNs
Early Stopping [1] [4] Halts the training process when performance on a validation set begins to degrade, preventing the model from over-optimizing on training data. Preventing Overfitting during Training
SMOTE (Synthetic Minority Over-sampling Technique) [7] Generates synthetic samples for minority classes to address class imbalance, preventing the model from underfitting to those classes. Mitigating Underfitting due to Imbalance
Quantile Uniform Transformation [7] Reduces feature skewness while preserving critical information (e.g., attack signatures in security data), improving model stability. Data Preprocessing for Better Fit

Overfitting and underfitting are not merely abstract concepts but are practical challenges that dictate the success of machine learning models in scientific research and drug development. The bias-variance tradeoff provides the theoretical underpinning, while rigorous methodological practices—such as cross-validation, regularization, and careful feature engineering—form the first line of defense. As evidenced by contemporary research, the choice of model complexity must be carefully matched to the quality and quantity of available data. For high-stakes fields like healthcare, a disciplined approach to managing model fit is non-negotiable. It is the cornerstone of developing reliable, generalizable, and trustworthy AI systems that can truly accelerate discovery and innovation.

The Critical Role of Generalization in Predictive Modeling

In the realm of machine learning, the ultimate test of a predictive model's value lies not in its performance on training data, but in its ability to make accurate predictions on new, unseen data. This capability is known as generalization [9]. For researchers and professionals in fields like drug development, where models must reliably inform critical decisions, achieving robust generalization is paramount. It represents the bridge between theoretical model performance and real-world utility [10].

The pursuit of generalization is fundamentally governed by the need to balance two opposing challenges: overfitting and underfitting. These concepts are central to a model's performance and are best understood through the lens of the bias-variance tradeoff [4] [11]. A model that overfits has learned the training data too well, including its noise and irrelevant details; it exhibits low bias but high variance, leading to excellent training performance but poor performance on new data [4] [12]. Conversely, a model that underfits has failed to capture the underlying patterns in the data; it exhibits high bias but low variance, resulting in suboptimal performance on both training and test sets [4] [11]. This technical guide explores the theoretical foundations, practical techniques, and experimental protocols for achieving generalization, with a particular focus on its critical importance in scientific research.

Theoretical Foundations: The Bias-Variance Tradeoff

The bias-variance tradeoff provides a fundamental framework for understanding generalization [4] [13].

  • Bias is the error arising from overly simplistic assumptions in the learning algorithm. A high-bias model is inflexible and may fail to capture complex patterns, leading to underfitting [4] [11]. For example, using a linear model to represent a non-linear relationship will typically result in high bias [11].
  • Variance is the error from sensitivity to small fluctuations in the training set. A high-variance model is overly complex and learns the noise in the training data as if it were a true pattern, leading to overfitting [4] [11].

The goal in machine learning is to find an optimal balance where both bias and variance are minimized, resulting in a model that generalizes well [4]. The following diagram illustrates the relationship between model complexity, error, and the concepts of overfitting and underfitting.

BiasVarianceTradeoff The Bias-Variance Tradeoff in Model Generalization CompoundError Total Prediction Error BiasSquared Bias² (Underfitting) CompoundError->BiasSquared Decreases with Complexity Variance Variance (Overfitting) CompoundError->Variance Increases with Complexity IrreducibleError Irreducible Error CompoundError->IrreducibleError Constant OptimalZone Optimal Generalization Zone UnderfitZone High Bias Zone OverfitZone High Variance Zone

Figure 1: The Bias-Variance Tradeoff. As model complexity increases, bias error decreases but variance error increases. The goal is to find the optimal complexity that minimizes total error, ensuring good generalization [4] [11] [13].

Techniques for Achieving Generalization

A suite of techniques has been developed to help models generalize effectively. The table below summarizes the primary methods used to combat overfitting and underfitting.

Table 1: Techniques to Improve Model Generalization

Technique Primary Target Mechanism of Action Common Algorithms/Examples
Regularization [9] [11] Overfitting Adds a penalty term to the loss function to discourage model complexity. Lasso (L1), Ridge (L2), Elastic Net
Cross-Validation [9] [11] Overfitting Rotates data splits for training/validation to ensure performance is consistent across subsets. k-Fold, Stratified k-Fold, Nested CV
Data Augmentation [9] [11] Overfitting Artificially expands the training set by creating modified versions of existing data. Image rotation/flipping, noise injection
Ensemble Methods [9] [13] Overfitting & Underfitting Combines predictions from multiple models to reduce variance and improve robustness. Random Forests, Bagging, Boosting
Dropout [4] [12] Overfitting Randomly "drops out" neurons during training to prevent co-adaptation. Neural Networks
Increase Model Complexity [4] [11] Underfitting Uses a more powerful model capable of learning complex patterns. Deep Neural Networks, Polynomial Features
Feature Engineering [4] [11] Underfitting Creates or selects more informative features to provide the model with better signals. Interaction terms, domain-specific transforms
The Generalization Workflow

Implementing these techniques effectively requires a structured workflow. The following diagram outlines a standard, iterative pipeline for building a generalized predictive model, incorporating key validation and tuning steps to mitigate overfitting and underfitting.

GeneralizationWorkflow Iterative Workflow for Building Generalized Models DataPrep Data Preparation & Feature Engineering InitialModel Initial Model Training DataPrep->InitialModel HyperTuning Hyperparameter Tuning & Regularization InitialModel->HyperTuning Eval Evaluation on Hold-Out Test Set HyperTuning->Eval Eval->DataPrep Validation Failure FinalModel Final Model Deployment Eval->FinalModel Validation Success CV K-Fold Cross-Validation CV->HyperTuning Reg Regularization (L1/L2/Dropout) Reg->HyperTuning Ensemble Ensemble Methods Ensemble->HyperTuning

Figure 2: Iterative Workflow for Building Generalized Models. This pipeline emphasizes the cyclical nature of model development, where failure to generalize on the test set necessitates a return to earlier stages for improvement [9] [11].

Experimental Protocols for Evaluating Generalization

Rigorous experimental design is non-negotiable for accurately assessing a model's ability to generalize. This is particularly critical in healthcare and drug development, where model failures can have significant consequences [10].

Case Study: Generalizing Clinical Text Models

A 2025 study published in Scientific Reports provides a robust template for evaluating generalization in a complex, real-world domain. The research aimed to classify anesthesiology Current Procedural Terminology (CPT) codes from clinical free text across 44 U.S. institutions [10].

Table 2: Key Experimental Components from Clinical Text Generalization Study [10]

Component Description Role in Generalization Research
Deep Neural Network (DNN) 3-layer architecture (500, 250, 48 units) with ReLU/Softmax and 25% dropout. Base predictive model to test generalization hypotheses.
Multi-Institution Data 1,607,393 procedures from 44 institutions, covering 48 CPT codes. Provides a real-world testbed for internal and external validation.
Text Preprocessing Levels Three tiers: "Minimal," "cSpell" (automated), and "Maximal" (physician-reviewed). Tests the impact of data cleaning on generalization.
Kullback-Leibler Divergence (KLD) Statistical measure of divergence between probability distributions of datasets. A heuristic to predict model performance on new institutional data.
k-Medoid Clustering Clustering algorithm applied to composite KLD metrics. Groups institutions by data similarity to understand generalization patterns.

Experimental Methodology:

  • Model Training Schemes: The researchers created and evaluated three types of models:
    • Single-Institution Models: Trained on one institution's data and tested on all others.
    • "All-Institution" Model: Trained on a combined 80% of data from all institutions and tested on the remaining 20%.
    • "Holdout" Models: Trained on data from 43 institutions and tested on the one held-out institution [10].
  • Performance Metrics: Accuracy and F1-score (micro-averaged) were used to compare predicted versus actual CPT codes [10].
  • Generalizability Assessment: The core of the experiment involved pairwise evaluation, where a model trained on one set of institutions was evaluated on data from a completely different set of institutions [10].

Quantitative Findings:

Table 3: Summary of Quantitative Results from Clinical Text Study [10]

Model Type Internal Data Performance (Accuracy/F1) External Data Performance (Accuracy/F1) Generalization Gap
Single-Institution 92.5% / 0.923 -22.4% / -0.223 Large performance drop, indicating poor generalization.
All-Institution -4.88% / -0.045 (vs. single) +17.1% / +0.182 (vs. single) Smaller gap; trades peak performance for better generalization.

The study concluded that while single-institution models achieved peak performance on their local data, they generalized poorly. In contrast, models trained on aggregated data from multiple institutions were significantly more robust to distributional shifts, despite a slight drop in internal performance [10]. This highlights a key trade-off in generalization research.

The Scientist's Toolkit: Research Reagents & Solutions

For researchers aiming to reproduce or build upon generalization experiments, the following table details key computational "reagents" and their functions.

Table 4: Essential Research Reagents for Generalization Experiments

Tool / Reagent Category Function in Generalization Research
K-Fold Cross-Validation [9] [11] Evaluation Framework Provides a robust estimate of model performance by rotating training and validation splits, reducing the variance of the performance estimate.
Kullback-Leibler Divergence (KLD) [10] Statistical Metric Quantifies the divergence between the probability distributions of two datasets (e.g., training vs. test, Institution A vs. Institution B), serving as a predictor of generalization performance.
Dropout [4] [12] Regularization Technique Prevents overfitting in neural networks by randomly disabling neurons during training, forcing the network to learn redundant representations.
L1 / L2 Regularization [4] [11] Regularization Technique Adds a penalty to the loss function (L1 for sparsity, L2 for small weights) to constrain model complexity and prevent overfitting.
Term Frequency-Inverse Document Frequency (TF-IDF) [10] Feature Engineering Converts unstructured text into a numerical representation, highlighting important words while downweighting common ones. Crucial for NLP generalization tasks.
Unified Medical Language System (UMLS) [10] Domain Knowledge Base A set of files and software that brings together key biomedical terminologies. Used in Informed ML to incorporate domain knowledge and improve generalization.

Generalization is the cornerstone of effective predictive modeling in research and industry. The challenge lies in navigating the bias-variance tradeoff to avoid the twin pitfalls of overfitting and underfitting. As demonstrated by both theoretical frameworks and rigorous clinical experiments, achieving generalization requires a principled approach that combines technical strategies—like regularization and cross-validation—with robust experimental design that tests models on truly external data. For drug development professionals and scientists, embracing these practices is not merely an academic exercise; it is a necessary discipline for building trustworthy AI systems that can deliver reliable insights and drive innovation in the real world.

In the pursuit of building effective machine learning models, researchers and practitioners aim to develop systems that perform well on their training data and, more importantly, generalize effectively to new, unseen data. The central challenge in this pursuit lies in navigating the tension between two fundamental sources of error: bias and variance. This tradeoff represents a core dilemma in statistical learning and forms the theoretical foundation for understanding the phenomena of overfitting and underfitting [14].

Framed within a broader thesis on model generalization, this decomposition provides a mathematical framework for diagnosing why models fail and offers principled approaches for improvement. For professionals in fields like drug development, where predictive model performance can have significant implications, understanding these concepts is essential for building reliable, robust systems that can accurately predict molecular activity, patient responses, or compound properties [15].

This technical guide provides an in-depth examination of bias-variance decomposition, its mathematical foundations, practical implications for model selection, and experimental methodologies for evaluating these error sources in research contexts.

Theoretical Foundation: Defining Bias and Variance

Core Concepts and Mathematical Definitions

In statistical learning, we typically assume an underlying functional relationship between input variables ( X ) and output variables ( Y ), expressed as ( Y = f(X) + \varepsilon ), where ( \varepsilon ) represents irreducible noise with mean zero and variance ( \sigma^2 ) [14]. Given a dataset ( D ) sampled from this distribution, we aim to learn an estimator or model ( \hat{f}(X; D) ) that approximates the true function ( f(X) ).

The bias of a learning algorithm refers to the error introduced by approximating a real-world problem, which may be complex, by a simplified model [16] [14]. Formally, for a given input ( x ), the bias is defined as the difference between the expected prediction of our model and the true value:

[ \text{Bias}(\hat{f}(x)) = \mathbb{E}[\hat{f}(x)] - f(x) ]

High bias indicates that the model is missing relevant relationships between features and target outputs, a phenomenon known as underfitting [4].

Variance refers to the amount by which the model's predictions would change if it were estimated using a different training dataset [14]. It captures the model's sensitivity to specific patterns in the training data:

[ \text{Var}(\hat{f}(x)) = \mathbb{E}\left[(\mathbb{E}[\hat{f}(x)] - \hat{f}(x))^2\right] ]

High variance indicates that the model has learned the noise in the training data rather than just the signal, a condition known as overfitting [4].

The Bias-Variance Decomposition

The bias-variance tradeoff finds its mathematical expression in the decomposition of the mean squared error (MSE). For a given model ( \hat{f} ) and test point ( x ), the expected MSE can be decomposed as follows [16] [14]:

[ \begin{align} \mathbb{E}[(y - \hat{f}(x))^2] &= \text{Bias}(\hat{f}(x))^2 + \text{Var}(\hat{f}(x)) + \sigma^2 \end{align} ]

Where ( \sigma^2 ) represents the irreducible error stemming from noise in the data generation process [16]. This decomposition reveals that to minimize total error, we must balance both bias and variance, as reducing one typically increases the other.

Table 1: Components of Mean Squared Error

Component Mathematical Expression Interpretation
Bias² ( (\mathbb{E}[\hat{f}(x)] - f(x))^2 ) Error from overly simplistic assumptions
Variance ( \mathbb{E}[(\mathbb{E}[\hat{f}(x)] - \hat{f}(x))^2] ) Error from sensitivity to training data fluctuations
Irreducible Error ( \sigma^2 ) Noise inherent in the data generation process

The Bias-Variance Tradeoff and Model Behavior

Relationship to Overfitting and Underfitting

The concepts of bias and variance provide a formal framework for understanding overfitting and underfitting [14]. When a model has high bias, it makes strong assumptions about the data and is too simple to capture underlying patterns, leading to underfitting [15] [4]. Such models typically exhibit poor performance on both training and test data. Linear regression applied to nonlinear data is a classic example of a high-bias model [15].

Conversely, when a model has high variance, it is excessively complex and sensitive to fluctuations in the training data, leading to overfitting [14] [4]. These models often perform well on training data but generalize poorly to unseen data. Decision trees with no pruning and high-degree polynomial regression are examples of high-variance models [15].

Table 2: Characteristics of Model Fit Conditions

Condition Bias Variance Training Performance Test Performance
Underfitting High Low Poor Poor
Proper Fitting Moderate Moderate Good Good
Overfitting Low High Excellent Poor

Visualizing the Tradeoff

The following diagram illustrates the relationship between model complexity, error, the bias-variance tradeoff, their relationship to overfitting and underfitting:

bias_variance_tradeoff cluster_1 Model Behavior cluster_2 Error Components Underfitting Underfitting BiasError Bias² Underfitting->BiasError Optimal Optimal TotalError Total Error (Generalization Error) Optimal->TotalError Overfitting Overfitting VarianceError Variance Overfitting->VarianceError BiasError->TotalError VarianceError->TotalError IrreducibleError Irreducible Error IrreducibleError->TotalError Complexity Model Complexity (Increases →) Complexity->Underfitting Complexity->Optimal Complexity->Overfitting

As model complexity increases, bias decreases but variance increases [17]. The optimal model complexity is found at the point where the total error (the sum of bias², variance, and irreducible error) is minimized [14]. This point represents the best possible generalization performance for a given learning algorithm and dataset.

Quantitative Analysis Through Polynomial Regression

Experimental Framework

Polynomial regression provides an excellent experimental framework for demonstrating the bias-variance tradeoff [15]. By varying the degree of the polynomial, we can directly control model complexity and observe its effects on bias and variance.

Consider a scenario where the true underlying function is ( f(x) = \sin(2\pi x) ) but we observe noisy samples: ( y = f(x) + \varepsilon ), where ( \varepsilon \sim \mathcal{N}(0, \sigma^2) ). We fit polynomial regression models of varying degrees to different samples from this distribution.

Table 3: Model Performance Across Complexity Levels

Model Type Polynomial Degree Bias² Variance Total MSE Model Behavior
Linear Model 1 0.2929 (High) Low 0.2929 Underfitting
Polynomial Model 4 Moderate Moderate 0.0714 Optimal Balance
Complex Polynomial 25 Low 0.059 (High) ~0.059 Overfitting

Experimental Protocol

To quantitatively evaluate bias and variance in practice, researchers can implement the following experimental protocol [18]:

  • Dataset Creation: Generate a synthetic dataset with known underlying function plus noise, or use a real dataset with sufficient samples.

  • Data Partitioning: Split the data into training and test sets, ensuring representative distributions.

  • Model Training: Train multiple models of varying complexity (e.g., polynomial degrees 1, 2, ..., 25) on the training data.

  • Bootstrap Sampling: Create multiple bootstrap samples from the original training data.

  • Model Evaluation:

    • Train the same model architecture on each bootstrap sample
    • Generate predictions on the test set from each model
    • Calculate bias as the squared difference between the average prediction and true value
    • Calculate variance as the average squared difference between individual predictions and the average prediction

  • Error Calculation: Compute total error as the sum of bias², variance, and optional noise term.

This methodology allows researchers to quantify the bias-variance profile of different algorithms and select the optimal complexity for their specific problem [18].

Managing the Tradeoff: Methods and Techniques

Regularization Approaches

Regularization techniques modify the learning algorithm to reduce variance at the expense of a small increase in bias, typically leading to better overall generalization [15] [17].

Ridge Regression (L2 Regularization) adds a penalty term proportional to the square of the coefficients to the loss function [15] [17]:

[ \text{Loss}{\text{Ridge}} = \sum{i=1}^{n}(yi - \hat{y}i)^2 + \lambda\sum{j=1}^{p}\betaj^2 ]

This discourages overly large coefficients, effectively reducing model variance [15].

Lasso Regression (L1 Regularization) adds a penalty term proportional to the absolute value of the coefficients [15] [17]:

[ \text{Loss}{\text{Lasso}} = \sum{i=1}^{n}(yi - \hat{y}i)^2 + \lambda\sum{j=1}^{p}|\betaj| ]

This can drive some coefficients to exactly zero, performing feature selection in addition to variance reduction [15].

Elastic Net Regression combines both L1 and L2 regularization penalties, offering a balance between feature selection and coefficient shrinkage [17].

Ensemble Methods

Ensemble methods combine multiple models to reduce variance without substantially increasing bias [15].

Bagging (Bootstrap Aggregating) trains multiple instances of the same algorithm on different bootstrap samples of the training data and averages their predictions [15]. This approach is particularly effective for high-variance algorithms like decision trees [15].

Boosting builds models sequentially, with each new model focusing on the errors of the previous ones [15]. This can reduce both bias and variance but requires careful tuning to avoid overfitting.

Other Strategic Approaches

  • Cross-Validation: Using k-fold cross-validation provides a more robust estimate of model performance and helps select optimal complexity [15].
  • Early Stopping: In iterative algorithms, stopping training before convergence can prevent overfitting [4].
  • Feature Selection: Reducing the number of features can decrease variance [4].
  • Increasing Training Data: Adding more diverse training samples can help reduce variance without increasing bias [4].

For researchers implementing bias-variance analysis, the following tools and techniques are essential:

Table 4: Research Reagent Solutions for Bias-Variance Analysis

Tool/Technique Function Application Context
Bootstrap Sampling Generates multiple training datasets with replacement Estimating variance of learning algorithms
K-Fold Cross-Validation Provides robust performance estimation Model selection and hyperparameter tuning
Regularization (L1/L2) Constrains model complexity Variance reduction in high-dimensional problems
Ensemble Methods (Bagging/Boosting) Combines multiple models Variance reduction while maintaining low bias
Learning Curves Plots training/validation error vs. sample size Diagnosing high bias or high variance conditions
Polynomial Feature Expansion Controls model complexity Systematic study of bias-variance tradeoff

Implications for Drug Development and Research

In drug development research, where datasets are often high-dimensional and sample sizes may be limited, understanding and managing the bias-variance tradeoff is particularly important [19]. For example:

  • Predictive Modeling: When building QSAR (Quantitative Structure-Activity Relationship) models to predict compound activity, researchers must balance model complexity to ensure accurate predictions on novel chemical structures.

  • Biomarker Discovery: In high-dimensional omics data (genomics, proteomics), regularization techniques like LASSO can help identify the most relevant biomarkers while avoiding overfitting to noise in the data [19].

  • Clinical Trial Optimization: Predictive models for patient response must generalize beyond the trial population to be clinically useful, requiring careful bias-variance management.

The mean squared error framework provides a principled approach for model selection in these critical applications, ensuring that models are neither too simplistic to capture important biological relationships nor so complex that they capitalize on chance patterns in the training data [19].

The bias-variance decomposition provides a fundamental framework for understanding generalization in machine learning. By formally characterizing the sources of error that lead to overfitting and underfitting, this theoretical foundation informs practical strategies for model development and selection. For researchers in drug development and other scientific fields, applying these principles leads to more robust, reliable predictive models that can better withstand the test of real-world application. The ongoing challenge remains in finding the optimal balance specific to each dataset and problem domain, using the methodological toolkit outlined in this guide.

The translation of machine learning (ML) models from research to clinical practice represents a profound challenge, where the theoretical concepts of overfitting and underfitting manifest with direct consequences for patient care and medical decision-making. Overfitting occurs when a model learns patterns specific to the training data that do not generalize to the broader population, while underfitting results from overly simplistic models that fail to capture essential predictive relationships [2]. In healthcare applications, these are not merely statistical artifacts but fundamental determinants of whether a model will enhance clinical outcomes or potentially cause harm.

The high-dimensional nature of healthcare data, often characterized by many potential predictors relative to patient samples, creates an environment particularly susceptible to overfitting [2] [20]. Simultaneously, the heterogeneity of patient populations and variations in clinical practice across institutions threaten model generalizability. This technical review examines concrete case studies where these phenomena have directly impacted model performance, extracting lessons for researchers and clinicians working at the intersection of ML and healthcare.

Theoretical Framework: Overfitting and Underfitting in Clinical Context

Defining Generalization Error in Clinical Prediction Models

In clinical prediction modeling, performance must be understood through three distinct error measurements: training data error (error on the data used to derive the model), true generalization error (error on the underlying population distribution), and estimated generalization error (error estimated from sample data) [2]. The discrepancy between training error and true generalization error represents the overfitting component, which arises when models learn idiosyncrasies of the training sample that are not representative of the population.

The bias-variance tradeoff manifests uniquely in clinical settings. Underfitted models (high bias) may overlook clinically relevant predictors, while overfitted models (high variance) may identify spurious correlations that fail to generalize beyond the development cohort. The optimal balance depends on the clinical use case, with high-stakes decisions requiring more conservative approaches that prioritize reliability over maximal accuracy [2] [21].

Methodological Origins of Poor Generalization

Several methodological factors contribute to overfitting and underfitting in clinical prediction models. Imperfect study designs that do not adequately represent the target population can introduce sampling biases that become embedded in the model [2]. Error estimation procedures that do not properly separate training and testing phases, such as using the same data for feature selection and model evaluation, create overly optimistic performance estimates [2]. Additionally, model complexity that is not justified by the available sample size represents a common pathway to overfitting, particularly with powerful learners like deep neural networks [22].

G cluster_origins Origins of Poor Generalization cluster_manifestations Manifestations data Clinical Data Source bias Sampling Bias data->bias method Methodological Flaws bias->method complexity Excessive Model Complexity method->complexity uf Underfitting method->uf of Overfitting complexity->of clinical Clinical Consequences of->clinical uf->clinical

Case Studies in Clinical Prediction Models

Ovarian Malignancy Classification: Overfitting with Competitive Generalization

A study on ovarian tumor classification demonstrated the complex relationship between overfitting and generalization in random forest models. Researchers developed prediction models to classify ovarian tumors into five categories using clinical and ultrasound data. The random forest model achieved a nearly perfect Polytomous Discrimination Index of 0.93 on training data, significantly higher than logistic regression models (PDI 0.47-0.70), suggesting substantial overfitting [23].

Unexpectedly, during external validation, the random forest model maintained competitive performance (PDI 0.54) compared to other methods (PDI 0.41-0.55), despite the extreme overfitting indicators in training [23]. Visualization of the probability estimates revealed that the random forest learned "spikes of probability" around events in the training set, where clusters of events created broader peaks (signal) while isolated events created local peaks (noise) [23]. This case illustrates that near-perfect training performance does not necessarily preclude clinical utility, challenging conventional assumptions about overfitting.

Dynamic Mortality Prediction in Critical Care

A study developing deep learning models for dynamic mortality prediction in critically ill children, termed the "Criticality Index," highlighted challenges in model complexity and implementability. The model achieved good discrimination (AUROC >0.8) but faced criticism for its extreme complexity, incorporating numerous variables and different neural networks for each 6-hour time window [21].

A significant limitation was the absence of benchmarking against more parsimonious and interpretable models, making it difficult to determine whether the complexity was justified [21]. This case exemplifies the tension between model complexity and practical implementation, where over-engineered solutions may achieve competitive performance metrics while sacrificing the simplicity required for clinical adoption and trust.

In-Hospital Mortality Prediction: Feature Selection Impact

Research on in-hospital mortality prediction using the eICU Collaborative Research Database provided insights into how feature selection affects model performance and interpretation. Researchers trained XGBoost models using 20,000 distinct feature sets, each containing ten features, to assess how different combinations influence performance [20].

Table 1: Performance Variation Across Feature Combinations in Mortality Prediction

Metric Average Performance Best Performance Key Influential Features
AUROC 0.811 0.832 Age, admission diagnosis, mean blood pressure
AUPRC Varied across sets Highest with specific combinations Different features than AUROC

Despite variations in feature composition, models exhibited comparable performance across different feature sets, with age emerging as particularly influential [20]. This demonstrates that multiple feature combinations can achieve similar discrimination, suggesting that the common practice of identifying a single "optimal" feature set may be misguided. The study also revealed that feature importance rankings varied substantially across different combinations, challenging the reliability of interpretation methods when features are correlated [20].

Breast Cancer Metastasis Prediction: Hyperparameter Effects

An empirical study on feedforward neural networks for breast cancer metastasis prediction systematically evaluated how 11 hyperparameters influence overfitting and model performance [22]. Researchers conducted grid search experiments to quantify relationships between hyperparameter values and generalization gap.

Table 2: Hyperparameter Impact on Overfitting in Deep Learning Models

Hyperparameter Impact Direction on Overfitting Significance Level
Learning Rate Negative correlation High
Iteration-based Decay Negative correlation High
Batch Size Negative correlation High
L2 Regularization Negative correlation Medium
Momentum Positive correlation Medium
Epochs Positive correlation Medium
L1 Regularization Positive correlation Medium

The findings revealed that learning rate, decay, and batch size had more significant impacts on overfitting than traditional regularization techniques like L1 and L2 [22]. This emphasizes the importance of comprehensive hyperparameter tuning beyond conventional regularization approaches. The study also identified interaction effects between hyperparameters, such as between learning rate and momentum, where large momentum values combined with high learning rates particularly degraded performance [22].

Experimental Protocols and Methodologies

Systematic Evaluation of Feature Combinations

The in-hospital mortality study employed a rigorous protocol for evaluating feature combinations [20]:

  • Initial Feature Selection: 41 clinically relevant features were selected based on physiological importance and alignment with established scoring systems like APACHE IV.

  • Feature Reduction: The feature set was reduced to 20 using SHAP value importance rankings derived from cross-validated models.

  • Complementary Pair Generation: 10,000 complementary feature set pairs of size 10 were created through unordered sampling without replacement.

  • Model Training: XGBoost models were trained using an 80/20 train/test split with consistent partitioning across all experiments.

  • Performance Assessment: Models were evaluated using AUROC and AUPRC, with SHAP values used to interpret feature importance across different combinations.

This protocol enabled systematic assessment of how feature interactions affect model performance and interpretation, providing insights beyond what single-feature analysis can reveal.

Hyperparameter Grid Search Methodology

The breast cancer metastasis study implemented comprehensive grid search experiments [22]:

  • Hyperparameter Selection: 11 hyperparameters were selected for systematic evaluation: activation function, weight initializer, number of hidden layers, learning rate, momentum, decay, dropout rate, batch size, epochs, L1, and L2.

  • Value Ranges: Each hyperparameter was tested across a wide range of values to capture nonlinear relationships with model performance.

  • Model Training: Feedforward neural networks were trained using electronic health records data with consistent evaluation metrics.

  • Overfitting Quantification: The generalization gap was measured as the difference between training and test performance.

  • Interaction Analysis: Pairwise interactions between hyperparameters were evaluated to identify compounding effects.

This methodological approach enabled ranking of hyperparameters by their impact on overfitting and provided practical guidance for tuning clinical prediction models.

G cluster_risk Critical Points for Overfitting/Underfitting data Clinical Data Source (EHR, Registries, Wearables) prep Data Preprocessing (Handling missing values, outliers) data->prep featsel Feature Selection (Clinical relevance, Statistical methods) prep->featsel hp Hyperparameter Tuning (Grid search, Bayesian optimization) featsel->hp eval Model Evaluation (Internal/External validation) hp->eval impl Implementation Consideration (Integration, Usability) eval->impl

The Researcher's Toolkit: Essential Methodological Components

Table 3: Research Reagent Solutions for Clinical Prediction Modeling

Component Category Specific Tools/Methods Function in Mitigating Overfitting/Underfitting
Data Sources Electronic Health Records, Patient Registries, Wearable Devices Provides representative real-world data covering diverse populations
Feature Selection SHAP Value Analysis, Clinical Domain Knowledge, Univariate Screening Balances model complexity with predictive information
Algorithms XGBoost, Random Forest, Logistic Regression, Neural Networks Offers varying complexity-flexibility tradeoffs
Regularization Methods L1 (Lasso), L2 (Ridge), Dropout, Early Stopping Explicitly constrains model complexity to improve generalization
Interpretability Tools SHAP, LIME, Partial Dependence Plots Enables validation of clinical plausibility of learned patterns
Validation Frameworks Nested Cross-Validation, External Validation, Temporal Validation Provides unbiased performance estimation

Discussion and Synthesis

Cross-Cutting Themes and Recommendations

Across the case studies, several consistent themes emerge regarding the real-world consequences of overfitting and underfitting in clinical prediction models. First, performance metrics alone are insufficient for evaluating model readiness for clinical implementation. The ovarian cancer study demonstrated that models showing extreme overfitting on training data can still generalize competitively, while the mortality prediction studies revealed that multiple feature combinations can achieve similar discrimination through different pathways [20] [23].

Second, model interpretability and complexity directly impact clinical utility. The tension between complex "black box" models and simpler interpretable approaches represents a fundamental challenge in clinical ML [21]. When multiple models achieve similar performance (the "Rashomon effect"), preference should be given to interpretable, parsimonious models that align with clinical understanding [21].

Third, implementation feasibility must be considered from the earliest development stages. Complex models requiring extensive feature engineering or specialized data elements face substantial barriers to real-world adoption, with one study estimating implementation costs exceeding $200,000 for even simple models [21].

Future Directions and Clinical Translation

Advancing clinical prediction models requires addressing several persistent challenges. Prospective validation remains uncommon, with only 13% of implemented models being updated following deployment [24]. Standardized evaluation frameworks that assess not just discrimination but also calibration, clinical utility, and implementation feasibility are needed [21] [24]. Furthermore, regulatory science must evolve to provide clearer pathways for model validation and monitoring in clinical practice.

The case studies collectively demonstrate that understanding and addressing overfitting and underfitting extends beyond statistical considerations to encompass clinical relevance, implementation practicality, and sustainable integration into healthcare workflows. By learning from these real-world examples, researchers can develop more robust, generalizable, and ultimately impactful clinical prediction models.

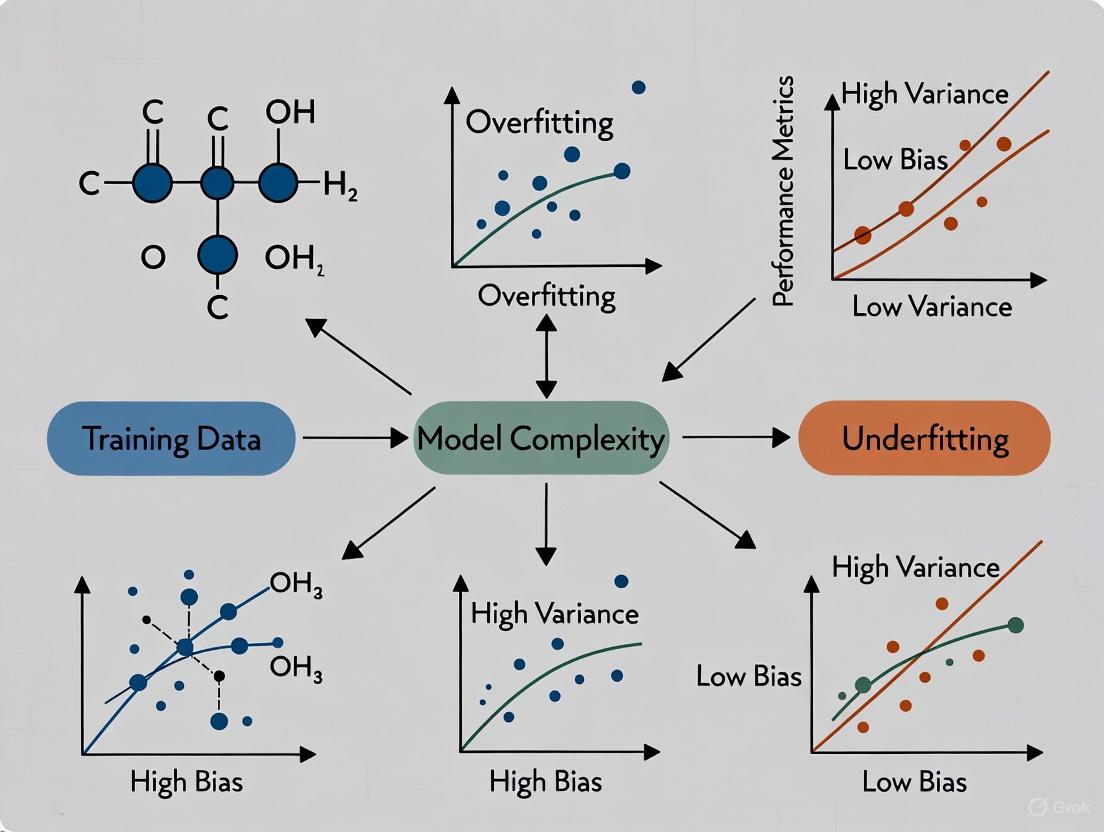
In machine learning, the Goldilocks Principle describes the critical goal of finding a model that is "just right"—neither too simple nor too complex [25] [26]. This principle directly addresses the core challenge of balancing overfitting and underfitting, two fundamental problems that determine a model's ability to generalize beyond its training data to new, unseen data [4] [11]. For researchers and drug development professionals, achieving this balance is not merely theoretical; it directly impacts the reliability and translational potential of predictive models in critical applications such as drug discovery, patient stratification, and treatment efficacy prediction.

The essence of the problem lies in the bias-variance tradeoff [25] [4]. Bias refers to error from erroneous assumptions in the learning algorithm, typically resulting in oversimplification. Variance refers to error from sensitivity to small fluctuations in the training set, resulting in over-complexity that captures noise as if it were signal [26] [11]. A model with high bias pays little attention to training data, leading to underfitting, while a model with high variance pays too much attention, leading to overfitting [4]. The idealized goal is to minimize both, creating a model that captures underlying patterns without memorizing dataset-specific noise [26].

Defining the Extremes: Overfitting and Underfitting

Conceptual Foundations and Symptoms

Overfitting occurs when a model is too complex and learns the training data too closely, including its noise and random fluctuations [25] [27]. Imagine a student who memorizes specific exam questions but fails to understand the underlying concepts; when question formats change, the student performs poorly [27]. An overfit model exhibits low bias but high variance [26] [11]. Key symptoms include:

  • Excellent performance on training data (low training error) [11]
  • Poor performance on validation and test data (high testing error) [4] [11]
  • Overly complex decision boundaries that adapt to noise [11]
  • Failure to generalize to new data from the same distribution [25]

In drug development, an overfit model might memorize specific experimental artifacts in training biomarker data rather than learning the true biological signatures of disease, failing when applied to new patient cohorts [11].

Underfitting occurs when a model is too simple to capture the underlying patterns in the data [25] [26]. This is akin to a student who only reads a textbook summary and misses crucial details needed to pass an exam [26]. An underfit model exhibits high bias but low variance [26] [11]. Key symptoms include:

  • Poor performance on both training and testing data [4] [11]
  • Consistently high errors across all datasets [11]
  • Inability to capture relevant relationships between features and target variables [25]
  • Systematic residual patterns indicating missed patterns [11]

In pharmaceutical research, underfitting might manifest as a linear model attempting to predict drug response based solely on dosage while ignoring crucial factors like genetic markers, metabolic pathways, and drug-drug interactions [11].

Visualizing the Tradeoff

The following diagram illustrates the relationship between model complexity, error, and the optimal "Goldilocks Zone" where a well-fit model achieves balance:

BiasVarianceTradeoff cluster_errors Error Title Bias-Variance Tradeoff and Model Complexity TotalError Total Error BiasError Bias Error TotalError->BiasError Decreases with complexity VarianceError Variance Error TotalError->VarianceError Increases with complexity Underfitting Underfitting Region GoldilocksZone 'Just Right' Goldilocks Zone Overfitting Overfitting Region ComplexityAxis Model Complexity → ErrorAxis Error →

Figure 1: The relationship between model complexity, bias, variance, and total error, showing the target "Goldilocks Zone."

Quantitative Evaluation Framework

Core Classification Metrics

Evaluating model fit requires robust metrics that reveal different aspects of performance. For classification problems common in biomedical research (e.g., disease classification, treatment response prediction), multiple metrics provide complementary insights [28] [29].

Table 1: Key Evaluation Metrics for Classification Models

Metric Formula Interpretation Use Case
Accuracy (TP+TN)/(TP+TN+FP+FN) [28] [29] Overall correctness Balanced datasets, equal cost of errors [29]
Precision TP/(TP+FP) [28] [29] How reliable positive predictions are When false positives are costly (e.g., drug safety) [29]
Recall (Sensitivity) TP/(TP+FN) [28] [29] Ability to find all positives When false negatives are costly (e.g., disease screening) [29]
F1-Score 2×(Precision×Recall)/(Precision+Recall) [28] [30] Balance of precision and recall Imbalanced datasets, single metric needed [29]
Specificity TN/(TN+FP) [30] Ability to identify negatives When correctly identifying negatives is crucial
AUC-ROC Area under ROC curve [28] [30] Overall discrimination ability Model selection across thresholds [28]

Regression and Model Performance Metrics

For regression problems (e.g., predicting drug dosage efficacy, patient survival time), different metrics quantify prediction errors:

Table 2: Key Evaluation Metrics for Regression Models

Metric Formula Interpretation Sensitivity
Mean Absolute Error (MAE) (1/N)∑⎮yj-ŷj⎮ [28] Average magnitude of errors Less sensitive to outliers
Mean Squared Error (MSE) (1/N)∑(yj-ŷj)² [28] Average squared errors Highly sensitive to outliers
Root Mean Squared Error (RMSE) √MSE [28] Standard deviation of errors More interpretable, same units
R-squared (R²) 1 - (∑(yj-ŷj)²/∑(y_j-ȳ)²) [28] Proportion of variance explained Goodness-of-fit measure

Diagnostic Tools and Visualization

Beyond single-number metrics, diagnostic visualizations provide deeper insights into model behavior and fit:

  • Learning Curves: Plot training and validation error against training set size or iteration. Overfit models show a large gap between curves; underfit models show convergence at high error [11].
  • Confusion Matrix: A tabular display of actual vs. predicted classifications, enabling detailed error analysis [28] [30].
  • ROC Curves: Plot true positive rate against false positive rate across classification thresholds, with AUC (Area Under Curve) quantifying overall performance [28] [30].
  • Residual Plots: For regression, plot differences between predicted and actual values to identify patterns suggesting underfitting [11].

Methodologies for Achieving Optimal Fit

Experimental Protocols and Techniques

Achieving the Goldilocks zone requires systematic experimentation with model architecture, training strategies, and data preparation. The following workflow provides a structured methodology:

ModelDevelopmentWorkflow cluster_diagnosis Diagnosis Phase Start 1. Problem Definition & Data Collection Eval 2. Establish Evaluation Framework Start->Eval Baseline 3. Develop Baseline Model Eval->Baseline Diagnose 4. Diagnose Fit Issues Baseline->Diagnose Address 5. Address Identified Issues Diagnose->Address HighTrainError High Training Error? Diagnose->HighTrainError Validate 6. Validate Final Model Address->Validate HighValError High Validation Error? HighTrainError->HighValError GoodFit Good Fit - Proceed to Validation HighTrainError->GoodFit No UnderfitConclusion Conclusion: Underfitting HighValError->UnderfitConclusion Yes OverfitConclusion Conclusion: Overfitting HighValError->OverfitConclusion No

Figure 2: A systematic workflow for diagnosing and addressing model fit issues.

The Scientist's Toolkit: Technical Solutions

Based on the diagnosis, researchers can select from a comprehensive toolkit of techniques to address specific fit issues:

Table 3: Research Reagent Solutions for Model Optimization

Technique Primary Use Mechanism Implementation Considerations
L1 & L2 Regularization [25] [11] Combat overfitting Adds penalty to loss function to constrain weights L1 (Lasso) promotes sparsity; L2 (Ridge) shrinks weights evenly
Dropout [25] [4] Neural network regularization Randomly disables neurons during training Prevents co-adaptation of features; effective in deep networks
Early Stopping [25] [4] Prevent overfitting Halts training when validation performance plateaus Monitors validation loss; requires separate validation set
Cross-Validation [11] Robust performance evaluation Splits data into k folds for training/validation Provides better generalization estimate; computational cost
Data Augmentation [25] [11] Improve generalization Artificially expands training data Domain-specific transformations; preserves label integrity
Ensemble Methods [4] [11] Improve predictive performance Combines multiple models Bagging reduces variance; boosting reduces bias
Feature Engineering [4] [11] Address underfitting Creates more informative features Domain knowledge crucial; can include interactions, polynomials

Advanced Protocol: Nested Cross-Validation for Robust Evaluation

For drug development applications where model reliability is critical, nested cross-validation provides a robust framework for both hyperparameter tuning and evaluation [11]:

  • Outer Loop: Split data into k-folds for performance estimation
  • Inner Loop: On each training fold, perform cross-validation to tune hyperparameters
  • Validation: Train with optimal hyperparameters on outer training fold, test on outer test fold
  • Iteration: Repeat across all outer folds, aggregate performance metrics

This approach prevents optimistic bias in performance estimates by keeping the test set completely separate from parameter tuning decisions [11].

Application in Drug Development and Pharmaceutical Research

Case Studies and Domain-Specific Considerations

The Goldilocks Principle finds critical application throughout drug development pipelines, where both over-optimistic and over-pessimistic models can have significant consequences:

  • Drug Dosage Optimization: Finding the therapeutic window between ineffective and toxic doses represents a literal Goldilocks problem. Models must balance underfitting that misses efficacy signals against overfitting that fails to generalize across patient populations [31] [11].

  • Biomarker Discovery: Predictive models for patient stratification must capture genuine biological signals without overfitting to batch effects or experimental noise. Underfit models miss clinically relevant biomarkers, while overfit models identify spurious correlations [11].

  • High-Throughput Screening: In virtual screening of compound libraries, models must generalize from limited training data to novel chemical spaces. Regularization and ensemble methods help maintain this balance [11].

Implementation Framework for Pharmaceutical Applications

Successful implementation requires domain-specific adaptations of the general methodologies:

  • Multi-Scale Validation: Validate models across biological replicates, experimental batches, and independent cohorts to ensure robustness.

  • Domain-Informed Regularization: Incorporate biological constraints (e.g., pathway information, chemical similarity) into regularization strategies.

  • Causality-Aware Modeling: Prioritize models that not only predict but provide mechanistic insights compatible with biological knowledge.

  • Regulatory-Compliant Evaluation: Maintain completely separate validation sets that simulate real-world deployment conditions, following FDA guidelines for algorithm validation.

The Goldilocks Principle provides both a philosophical framework and practical guidance for developing machine learning models that generalize effectively to new data. By systematically diagnosing and addressing overfitting and underfitting through appropriate evaluation metrics, regularization strategies, and validation protocols, researchers can create models that are "just right" for their intended applications. In drug development and pharmaceutical research, where predictive accuracy directly impacts patient outcomes and therapeutic discoveries, mastering this balance is not merely technical excellence but an ethical imperative. The methodologies and frameworks presented here provide a roadmap for achieving models that are sufficiently complex to capture meaningful patterns while remaining sufficiently simple to generalize beyond their training data.

Fit-for-Purpose Modeling: Techniques and Applications in Drug Development

Aligning Model Complexity with Context of Use (COU) in MIDD

Model-Informed Drug Development (MIDD) is an essential framework that uses quantitative methods to accelerate hypothesis testing, improve efficiency in assessing drug candidates, reduce costly late-stage failures, and support regulatory decision-making [32]. A core principle in MIDD is the "fit-for-purpose" (FFP) approach, which strategically aligns model development and complexity with a specific Context of Use (COU) and key Question of Interest (QOI) [32]. This alignment is critical; an overly complex model may become a "black box," difficult to validate and interpret, while an overly simplistic one may fail to capture essential biology or pharmacology, leading to poor predictive performance and misguided decisions [32] [1].

The following diagram illustrates the fundamental relationship between model complexity and the specific Context of Use within the MIDD paradigm.

COU Context of Use (COU) Early Early Discovery & Target ID COU->Early Preclinical Preclinical Research COU->Preclinical Clinical Clinical Development COU->Clinical PostMarket Post-Market Surveillance COU->PostMarket Complexity Model Complexity Low Low Complexity (e.g., QSAR, NCA) Early->Low Medium Medium Complexity (e.g., PBPK, PopPK) Preclinical->Medium High High Complexity (e.g., QSP, AI/ML) Clinical->High PostMarket->Medium

Figure 1: The Alignment of Model Complexity with Drug Development Stage and Context of Use. The appropriate level of model complexity is determined by the specific stage of drug development and its corresponding Context of Use (COU), ranging from simpler models in early discovery to highly complex models for clinical development.

The "Fit-for-Purpose" Framework: Core Principles

Defining Context of Use (COU) and Question of Interest (QOI)

The Context of Use (COU) is a formal definition that describes the specific role and scope of a model—how its predictions will inform a particular decision in drug development or regulatory evaluation [32]. The COU is intrinsically linked to the Question of Interest (QOI), the precise scientific or clinical question the model is built to answer [32]. A well-defined COU specifies the model's purpose, the decisions it supports, and the applicable boundaries, ensuring the modeling effort is targeted and impactful.

A model is considered not FFP if it fails to define the COU, suffers from poor data quality, or lacks proper verification and validation. Oversimplification, insufficient data, or unjustified complexity can also render a model unfit for its intended purpose [32].

The Spectrum of Model Complexity in MIDD

MIDD employs a wide array of quantitative tools, each with its own level of complexity and appropriate application. The following table summarizes the key MIDD methodologies and their primary characteristics.

Table 1: Key Methodologies in Model-Informed Drug Development (MIDD)

Methodology Description Primary Applications in Drug Development Typical Complexity Level
Quantitative Structure-Activity Relationship (QSAR) [32] Computational modeling predicting biological activity from chemical structure. Early target identification, lead compound optimization. Low
Non-Compartmental Analysis (NCA) [32] Model-independent estimation of PK parameters (exposure, clearance). Initial PK analysis from rich plasma concentration-time data. Low
Physiologically Based Pharmacokinetic (PBPK) [32] Mechanistic modeling simulating drug disposition based on physiology and drug properties. Predicting drug-drug interactions, formulation impact, First-in-Human (FIH) dose prediction. Medium
Population PK (PPK) & Exposure-Response (ER) [32] Models explaining variability in drug exposure and linking exposure to efficacy/safety outcomes. Optimizing dosing regimens, informing clinical trial design, supporting label claims. Medium
Quantitative Systems Pharmacology (QSP) [32] Integrative, mechanistic modeling of drug effects within biological system networks. Predictive safety evaluation, target validation, identifying critical biomarkers. High
AI/ML Approaches [33] [3] Data-driven models learning complex patterns from large datasets (e.g., bioactivity prediction, molecular design). Drug target associations, biomarker discovery, de novo molecular design, predictive ADMET. High

Aligning Model Complexity with Drug Development Stages

Early Discovery and Preclinical Development

In early stages, the COU often involves rapid screening and prioritization. Models are used to filter thousands of potential candidates, requiring interpretability and speed over high predictive precision for human outcomes [32] [33].

  • Typical QOIs: "Which chemical series shows the most promise for potency?" or "What is the predicted human PK profile?"
  • FFP Models: QSAR models are ideal for predicting structure-activity relationships [32]. Machine Learning models trained on public and proprietary data can predict absorption, distribution, metabolism, and excretion (ADME) properties, significantly accelerating lead optimization [33] [3].
  • Complexity Consideration: While some ML models can be complex, their use here is FFP because they are applied to high-volume, early-stage prioritization where the cost of error is lower. The focus is on low bias to avoid missing promising compounds (underfitting), accepting that some false positives may occur [1].
Clinical Development and Regulatory Submissions

During clinical development, the COU shifts to informing study designs and dosing strategies, with a greater need for models that can extrapolate to human populations and support regulatory decisions [32] [34].

  • Typical QOIs: "What is the recommended Phase 2 dose?" or "How will renal impairment affect drug exposure?"
  • FFP Models: PBPK models are FFP for predicting drug-drug interactions and FIH doses [32]. Population PK/ER models are central to understanding sources of variability in drug response and justifying dosing recommendations [32].
  • Complexity Consideration: These medium-complexity models are justified because they incorporate known physiology and population variability. The FDA's MIDD Paired Meeting Program highlights regulatory acceptance of these approaches for dose selection and trial simulation [34]. The primary risk is overfitting the model to sparse early clinical data, which can be mitigated by using prior knowledge and external validation [32] [1].
Confirmatory Trials and Post-Market Surveillance

For late-stage and post-market decisions, the COU often involves generating evidence to support specific label claims or optimizing use in real-world populations. The consequence of an incorrect model prediction is high, requiring robust validation [32].

  • Typical QOIs: "Can we justify a new patient population in the label?" or "What is the potential effectiveness of a new combination therapy?"
  • FFP Models: QSP models, which are highly complex and mechanistic, can be FFP for exploring combination therapies or long-term outcomes where clinical trials are unethical or impractical [32]. Model-based meta-analyses (MBMA) integrate data across multiple trials to provide context for a new drug's performance.
  • Complexity Consideration: The high complexity of QSP is warranted by the complex QOI. The key is to manage the risk of overfitting by ensuring the model is grounded in established biology and calibrated against multiple data sources [32].

A Practical Framework for Risk Assessment and Model Selection

Selecting a FFP model requires a structured assessment of the decision at hand. The following workflow provides a methodological approach for researchers to align model complexity with COU while mitigating risks of overfitting and underfitting.

Start 1. Define QOI and COU A 2. Assess Decision Consequence - What is the impact of a wrong prediction? Start->A B 3. Assess Model Influence - What weight will the model carry in the totality of evidence? A->B C Consequence of an incorrect decision? B->C D Model Influence on decision? C->D Medium or High E Lower Complexity Model C->E Low F Medium Complexity Model D->F Supporting/Informative G Higher Complexity Model (Rigorous Validation Required) D->G Substantial/Decisive H 4. Implement Model with Appropriate Validation Plan E->H F->H G->H

Figure 2: A Risk-Based Workflow for "Fit-for-Purpose" Model Selection. This decision process guides the selection of appropriate model complexity by evaluating the consequence of an incorrect prediction and the model's intended influence on the final decision.

The FDA emphasizes that the model risk assessment should consider both the weight of model predictions in the totality of data (model influence) and the potential risk of making an incorrect decision (decision consequence) [32] [34]. The following table outlines a framework for this assessment.

Table 2: Risk Assessment Framework for MIDD Model Selection and Validation

Decision Consequence Model Influence Recommended FFP Model Complexity & Key Actions Primary ML Pitfall to Mitigate
Low (e.g., internal compound prioritization) Supporting (one of several evidence sources) Lower Complexity. Use well-established, interpretable models (e.g., QSAR, linear regression). Limited validation may be sufficient. Underfitting (high bias). Ensure the model is sufficiently complex to capture the real signal in the data. [1]
Medium (e.g., informing Phase 2 dose) Informative (guides design but not sole evidence) Medium Complexity. Use models with mechanistic basis (e.g., PBPK, PopPK). Requires internal and potentially external validation. Overfitting (high variance). Use techniques like cross-validation and regularization to ensure generalization. [1] [3]
High (e.g., primary evidence for a regulatory decision) Substantial/Decisive (critical evidence for a key claim) Higher Complexity. Use of QSP or complex ML is permissible but requires extensive validation, documentation, and external verification. A comprehensive analysis of uncertainty is mandatory. [32] [34] Overfitting and lack of interpretability. Employ sensitivity analysis, uncertainty quantification, and methods like SHAP to explain predictions. [1] [35]

Experimental Protocols for Model Validation

Ensuring a model is FFP requires rigorous experimental protocols for validation. These methodologies are critical for diagnosing and preventing both overfitting and underfitting.

Protocol for Diagnosing and Mitigating Overfitting

Objective: To assess whether a model has learned the training data too well, including its noise, and fails to generalize to new data. This is a common risk with complex models like deep neural networks and QSP models with many unidentifiable parameters [1] [3].

Methodology:

  • Data Splitting: Partition the available dataset into a training set (e.g., 70-80%) and a hold-out test set (e.g., 20-30%). The test set must not be used for any aspect of model training or parameter tuning [3].
  • Resampling and Cross-Validation: Use k-fold cross-validation (e.g., k=5 or 10) on the training set. This involves splitting the training data into k folds, training the model on k-1 folds, and validating on the remaining fold, repeating the process k times. This provides a robust estimate of model performance on unseen data and helps tune hyperparameters without leaking information from the test set [1].
  • Apply Regularization Techniques: Introduce penalties for model complexity during training.
    • L1 Regularization (Lasso): Adds a penalty equal to the absolute value of coefficient magnitudes, which can shrink less important coefficients to zero, performing feature selection. [1] [3]
    • L2 Regularization (Ridge): Adds a penalty equal to the square of coefficient magnitudes, forcing weights to be small but rarely zero. [1] [3]
    • Dropout (for Neural Networks): Randomly ignores a percentage of neurons during training, preventing complex co-adaptations and forcing the network to learn more robust features. [3]
  • Performance Comparison: Calculate key performance metrics (e.g., R², RMSE for regression; AUC, accuracy for classification) on both the training and test sets. A significant performance drop on the test set is a hallmark of overfitting [1].
  • Early Stopping: For iterative models like neural networks, monitor performance on a validation set during training. Halt training when validation performance begins to degrade, even if training performance continues to improve [1].
Protocol for Diagnosing and Mitigating Underfitting

Objective: To determine if a model is too simple to capture the underlying structure of the data, resulting in poor performance on both training and test data. This is a risk with overly simplistic models applied to complex problems [1].

Methodology:

  • Baseline Performance Analysis: Train a simple model (e.g., linear model) and evaluate its performance on the training data. If performance is unacceptably poor, it is a strong indicator of underfitting [1].
  • Model Complexity Increase: Iteratively increase model complexity.
    • Add Relevant Features: Engineer new features or include previously excluded variables that may have predictive power. [1]
    • Use More Complex Algorithms: Switch from a linear model to a polynomial model, decision tree, or ensemble method. [1]
  • Reduce Regularization: If regularization was applied, reduce the regularization hyperparameter to allow the model greater flexibility to fit the data [1].
  • Error Analysis: Analyze the residuals (difference between predictions and actual values). If residuals show a non-random pattern (e.g., a curve), it suggests the model is missing a key relationship in the data [1].
  • Feature Importance Check: Use techniques like permutation importance or tree-based feature importance scores to ensure key predictive features are being utilized effectively by the model [35].

The Scientist's Toolkit: Essential Research Reagent Solutions

The following table details key computational and methodological "reagents" essential for implementing FFP modeling in MIDD.

Table 3: Essential Research Reagent Solutions for MIDD

Tool / Resource Function in FFP Modeling Relevance to Over/Underfitting
Scikit-learn [3] A comprehensive Python library providing simple and efficient tools for data mining and analysis. Includes implementations of many classic ML algorithms, preprocessing tools, and model validation techniques like cross-validation. Essential for implementing standardized validation workflows to detect overfitting and for comparing multiple model complexities to avoid underfitting.
TensorFlow & PyTorch [3] Open-source libraries for numerical computation and large-scale machine learning, specializing in defining, training, and running deep neural networks. Provides built-in functions for dropout and other regularization techniques to mitigate overfitting in complex models. Allows for flexible model architecture design to combat underfitting.
ColorBrewer & Accessibility Tools [36] [37] Scientifically developed color schemes for maps and visualizations that are perceptually uniform and colorblind-safe. Critical for creating honest and accessible visualizations of model diagnostics (e.g., residual plots, validation curves) to prevent misinterpretation of model performance.
k-Fold Cross-Validation [1] [3] A resampling procedure used to evaluate models by partitioning the data into k subsets, training on k-1 subsets, and validating on the remaining one. A core technique for obtaining a reliable estimate of model generalization error, which is the primary metric for diagnosing overfitting.
SHAP (SHapley Additive exPlanations) [35] A game theory-based method to explain the output of any machine learning model. It quantifies the contribution of each feature to a single prediction. Enhances interpretability of complex models, helping to build trust and identify if the model is relying on spurious correlations (a sign of overfitting) or meaningful features.
Model-Informed Drug Development Paired Meeting Program [34] An FDA initiative that allows sponsors to meet with Agency staff to discuss MIDD approaches in a specific drug development program. Provides a formal pathway for aligning the planned model's complexity and COU with regulatory expectations early in development, de-risking the overall strategy.

Success in MIDD hinges on the disciplined application of the "fit-for-purpose" principle. There is no universal "best" model—only the model that is optimally aligned with the Context of Use, adequately addresses the Question of Interest, and is rigorously validated for its intended task. By systematically assessing decision consequence and model influence, leveraging appropriate experimental protocols for validation, and utilizing the modern toolkit of software and regulatory pathways, drug developers can strategically navigate the trade-offs between underfitting and overfitting. This disciplined approach maximizes the potential of MIDD to streamline development, reduce attrition, and ultimately deliver safe and effective therapies to patients more efficiently.

The pursuit of robust, predictive models is a central challenge in modern drug development. Researchers employ a spectrum of sophisticated methodologies, including Quantitative Systems Pharmacology (QSP), Physiologically-Based Pharmacokinetic (PBPK) modeling, and Artificial Intelligence/Machine Learning (AI/ML). Each approach offers a distinct strategy for understanding the complex interplay between drugs and biological systems. A critical consideration that transcends all these methodologies is the machine learning concept of the bias-variance tradeoff, manifesting as underfitting (high bias) or overfitting (high variance). A model that underfits is too simplistic to capture the underlying biological or chemical patterns, leading to poor predictive performance on all data. In contrast, a model that overfits has memorized the noise and specificities of its training data, failing to generalize to new, unseen datasets or real-world scenarios. This guide explores these core modeling frameworks, their interrelationships, and the practical strategies researchers use to navigate the critical path between underfitting and overfitting to build reliable, translatable models.

Core Modeling Methodologies

The landscape of computational modeling in pharmacology is diverse, with each approach serving a unique purpose and operating at a different level of biological abstraction. The following table summarizes the defining characteristics of QSP, PBPK, and AI/ML models.

Table 1: Comparison of Core Modeling Methodologies in Drug Development

Feature QSP (Quantitative Systems Pharmacology) PBPK (Physiologically-Based Pharmacokinetic) AI/ML (Artificial Intelligence/Machine Learning)
Primary Focus Understanding drug-body interactions within a systems biology context, often linking pharmacokinetics (PK) to pharmacodynamics (PD) [38] [39]. Predicting drug concentration-time profiles in plasma and various tissues based on physiology, physicochemical properties, and biology [38] [39]. Identifying complex patterns in high-dimensional data for prediction and optimization across the drug development pipeline [40].
Core Approach Mechanistic, "middle-out" Mechanistic, "bottom-up" Data-driven, "top-down"
Typical Applications Target identification, biomarker evaluation, preclinical-to-clinical translation, combination therapy optimization [39]. Predicting drug-drug interactions (DDIs), formulation impact, dose selection in special populations, virtual bioequivalence [38]. Molecular design & virtual screening, drug repurposing, predicting toxicity & bioactivity, clinical trial patient stratification [40].
Key Strength Ability to extrapolate beyond collected data and interrogate biological systems [38]. Incorporates physiological parameters, enabling interspecies scaling and population predictions [38]. High predictive power for specific tasks with sufficient high-quality data; handles complex, non-linear relationships [40].
Inherent Fitting Risk Risk of underfitting if the model is too simplistic and omits key biological pathways crucial to the disease or drug effect. Risk of underfitting if the model lacks key physiological compartments or processes relevant to the drug's disposition. High risk of overfitting, especially with complex models (e.g., deep learning) on limited datasets, leading to poor generalization [1] [4] [41].

Quantitative Systems Pharmacology (QSP)

QSP models are mechanistic constructs designed to quantitatively represent biological, toxicological, or disease processes in response to therapeutic intervention [38]. Unlike purely data-driven models, the primary objective of a QSP model is to achieve a systems-level understanding, with less emphasis on perfectly describing a specific dataset. A key application is their integration with PBPK models to create a holistic platform that can simulate a drug's journey from administration to tissue distribution and final physiological effect [39]. For instance, a coupled PBPK-QSP model can be developed for mRNA-based therapeutics, where the PBPK component predicts liver disposition of the lipid nanoparticle (LNP), while the QSP component models the subsequent intracellular mRNA translation into a therapeutic protein and its resulting pharmacodynamic effect [39].

Physiologically-Based Pharmacokinetic (PBPK) Modeling

PBPK models are a form of quantitative systems pharmacokinetics that leverage physiological and anatomical information to simulate a drug's absorption, distribution, metabolism, and excretion (ADME). These models compartmentalize the body into organs and tissues connected by blood flow, with drug movement described using mass balance equations [38] [39]. A major paradigm shift enabled by PBPK modeling is the separation of drug-specific parameters (e.g., tissue permeability) from system-specific parameters (e.g., organ blood flow rates). This separation, facilitated by in vitro-in vivo extrapolation (IVIVE), allows for a "bottom-up" predictive approach and enables extrapolation beyond the conditions of initial clinical studies, moving the development process from a traditional "learn-confirm" cycle to a more powerful "predict-learn-confirm-apply" cycle [38].

Artificial Intelligence and Machine Learning (AI/ML)

AI, particularly its subset ML, refers to systems that use machine- and human-based inputs to perceive environments, abstract these perceptions into models, and use model inference to formulate options for information or action [42]. In drug development, ML models are predominantly data-driven and developed using robust statistical algorithms to describe observed data [38]. These models excel at finding complex patterns in large datasets, such as predicting the binding affinity of small molecules, generating novel drug-like compounds, or identifying patients for clinical trials from electronic health records [40]. The FDA has recognized a significant increase in drug application submissions using AI/ML components, highlighting its growing importance [42].

The Central Paradigm: Overfitting and Underfitting

The performance and utility of any model, whether a mechanistic QSP construct or a deep neural network, are governed by its ability to generalize. This is conceptualized through the bias-variance tradeoff.

  • Underfitting (High Bias): This occurs when a model is too simple to capture the underlying patterns in the data. An underfit model performs poorly on both the training data and new, unseen data [1] [4] [41]. In the context of PBPK modeling, this could be a model that lacks a key tissue compartment involved in the drug's distribution, leading to consistently poor predictions across all datasets. It fails to "learn" the true system.
  • Overfitting (High Variance): This occurs when a model is excessively complex and learns not only the underlying signal but also the noise and random fluctuations in the training data [1] [4]. An overfit model will perform exceptionally well on its training data but fail to generalize to new data. This is a predominant risk in AI/ML, where a model with millions of parameters might "memorize" a limited dataset of molecular structures instead of learning the general rules of binding.

Table 2: Diagnosing and Addressing Underfitting and Overfitting

Aspect Underfitting Overfitting
Performance Poor on both training and test data [1] [4]. Excellent on training data, poor on unseen test data [1] [4].
Model Complexity Too simple for the problem [1]. Too complex for the available data [1].
Analogy A student who only read chapter titles [1]. A student who memorized the textbook verbatim [41].
Common Causes Oversimplified model, insufficient features, excessive regularization [1] [4]. Overly complex model, insufficient training data, noisy data [1] [4].
Remedial Strategies Increase model complexity, add informative features, reduce regularization [1] [4] [43]. Gather more high-quality data, apply regularization (L1/L2, dropout), use cross-validation, implement early stopping [1] [4] [41].

The following diagram illustrates the logical workflow for developing and validating a model while actively managing the risks of underfitting and overfitting. This process is applicable across QSP, PBPK, and AI/ML methodologies.

FittingBalance Start Start with a Simple Model Diagnose Diagnose with Validation Set Start->Diagnose UnderfitDecision Underfitting? Diagnose->UnderfitDecision OverfitDecision Overfitting? UnderfitDecision->OverfitDecision No IncreaseComplexity Increase Model Complexity • Add biological mechanisms (QSP/PBPK) • Add layers/neurons (AI/ML) • Engineer new features UnderfitDecision->IncreaseComplexity Yes ApplyRegularization Apply Regularization • Simplify model structure • Use L1/L2 regularization (AI/ML) • Use cross-validation OverfitDecision->ApplyRegularization Yes Optimal Optimal Fit Achieved OverfitDecision->Optimal No IncreaseComplexity->Diagnose ApplyRegularization->Diagnose

Model Fitting Optimization Workflow

Methodologies and Experimental Protocols

Parameter Estimation in PBPK and QSP Models

Parameter estimation is the process of calibrating a model to observed data, a step critical for ensuring model credibility. For complex PBPK and QSP models, this involves using algorithms to find the parameter values that minimize the difference between model simulations and experimental observations.

Table 3: Common Parameter Estimation Algorithms for PBPK/QSP Models [44]

Algorithm Description Best Suited For
Quasi-Newton Method Uses an approximation of the Hessian matrix to find the minimum of a function. Efficient for local searches. Models with smooth, continuous parameter spaces where good initial estimates are available.
Nelder-Mead Method A direct search simplex method that does not require derivatives. Robust but can be slow. Complex models where derivative calculation is difficult or computationally expensive.
Genetic Algorithm (GA) An evolutionary-inspired global optimization method that uses selection, crossover, and mutation. Complex, multi-modal problems where the parameter space is large and the global minimum is difficult to find.
Particle Swarm Optimization (PSO) A global optimization technique inspired by social behavior, like bird flocking. Particles "fly" through the parameter space. Similar applications to GA; often effective for exploring complex parameter landscapes.
Cluster Gauss-Newton Method (CGN) A deterministic method designed for least-squares problems that can handle multiple local minima. High-dimensional, complex models typical of QSP and large-scale PBPK models.

A critical best practice is to not rely on a single algorithm or a single set of initial parameter values. Research indicates that the performance of these algorithms is highly dependent on the model's structure and the specific parameters being estimated. To obtain credible and robust parameter estimates, it is advisable to conduct multiple rounds of estimation using different algorithms and initial values [44].

A Protocol for Developing a Minimal PBPK-QSP Platform

The following protocol outlines the key steps for developing a coupled PBPK-QSP model, as demonstrated in a study for LNP-mRNA therapeutics [39].

  • Model Structuring and System Definition:

    • Define the scope and the key research question (e.g., "How does LNP design influence hepatic protein expression and duration of effect?").
    • Structure the PBPK component with physiologically relevant compartments (e.g., venous blood, arterial blood, liver, portal organs, lymph nodes). Each tissue compartment is further divided into sub-compartments (vascular, interstitial, cellular) [39].
    • Structure the QSP component to capture the key intracellular events: cellular uptake of the LNP, LNP degradation, mRNA escape from the endosome, mRNA translation into protein, and protein-dependent pharmacodynamic effect [39].

  • Parameterization and Input:

    • System Parameters: Incorporate known physiological parameters (e.g., tissue volumes, blood flow rates) from the literature [39].
    • Drug/System-Specific Parameters: Obtain parameters from in vitro assays (e.g., mRNA stability, translation rate, LNP degradation rate) or from literature-based estimates. This is where IVIVE is critical.

  • Model Calibration and Qualification:

    • Use parameter estimation algorithms (see Table 3) to calibrate the model against observed in vivo data (e.g., plasma mRNA PK, tissue distribution data, protein expression time-courses).
    • Perform a sensitivity analysis to identify the model parameters that most significantly influence the key outputs (e.g., protein exposure). In the LNP-mRNA model, mRNA stability and translation rate were highly sensitive, whereas liver influx rate was not [39].
    • Qualify the model by establishing its credibility for its intended use, which may involve testing its predictive performance against a separate dataset not used for calibration [38].

  • Model Simulation and Application:

    • Use the qualified model to run simulations and generate hypotheses. For example, the LNP-mRNA model was used to simulate how tuning the mRNA degradation rate could optimize protein exposure and how LNP recycling could lead to a second peak in plasma mRNA concentrations [39].
    • Create virtual animal or human cohorts to explore optimal dosing regimens and reduce dosing frequency while maintaining efficacy [39].

Table 4: Essential Software and Resources for Implementing Advanced Models

Tool/Resource Type Function in Research
Simcyp Simulator Commercial PBPK Platform Provides a robust environment for PBPK modeling and simulation, including population-based ADME prediction and drug-drug interaction risk assessment [38].
R with mrgsolve Open-Source Software Package A free, open-source platform (mrgsolve) within the R programming language specifically designed for ODE-based model development, supporting both PBPK and QSP models [45].
AlphaFold AI System Predicts protein structures with high accuracy, dramatically accelerating target identification and drug design by providing reliable protein models for virtual screening [40].
Generative Adversarial Networks (GANs) AI/ML Algorithm Used in molecular modeling to generate novel chemical entities with desired physicochemical and biological properties, expanding the available chemical space for drug candidates [40].
K-Fold Cross-Validation Model Validation Technique A core method for assessing model generalizability and combating overfitting by partitioning data into 'k' subsets for repeated training and validation [1] [43].

The integration of QSP, PBPK, and AI/ML represents a powerful, multi-faceted approach to modernizing drug development. QSP and PBPK models provide a mechanistic, physiologically-grounded framework that excels at extrapolation and systems-level inquiry, though they risk underfitting if key mechanisms are omitted. AI/ML models offer unparalleled power in pattern recognition and prediction from large datasets but are highly susceptible to overfitting, which can render them useless in real-world applications. The path to success lies in a thoughtful integration of these approaches, guided by a rigorous understanding of the bias-variance tradeoff. By employing robust parameter estimation techniques, rigorous model qualification and verification, and modern validation methods like cross-validation, researchers can build predictive models that successfully navigate the narrow path between underfitting and overfitting. This, in turn, accelerates the delivery of safe and effective therapies to patients.

Addressing Data Scarcity and Imbalance in Clinical Datasets

In clinical machine learning, the twin challenges of data scarcity and class imbalance are not merely logistical hurdles but fundamental drivers of model underperformance, directly leading to overfitting and underfitting. Data scarcity, common in rare disease studies or emerging health threats, forces models to make sweeping generalizations from insufficient examples, resulting in underfitting and poor predictive accuracy [46]. Conversely, severe class imbalance—where rare conditions are vastly outnumbered by normal cases—often causes models to develop biased decision boundaries that appear precise on training data but fail to generalize to real-world clinical populations, a classic symptom of overfitting [2] [11].

The bias-variance tradeoff manifests acutely in clinical datasets. High-bias models underfit by oversimplifying complex pathological patterns, while high-variance models overfit by learning spurious correlations and dataset-specific noise [11]. This whitepaper provides clinical researchers and drug development professionals with technically robust methodologies to navigate these challenges, ensuring developed models achieve optimal fit for reliable clinical application.

Technical Approaches for Data Scarcity

Advanced Data Augmentation and Synthetic Generation

Synthetic data generation has emerged as a pivotal solution for data scarcity, creating artificial datasets that preserve the statistical properties of original clinical data without containing real patient information [47]. The growing adoption of synthetic data is driven by generative AI advancements, privacy regulations (GDPR, HIPAA), and the need for scalable data solutions [48].

Table 1: Synthetic Data Generation Methods in Healthcare

Method Category Specific Techniques Clinical Data Applications Key Considerations
Deep Learning-Based Generative Adversarial Networks (GANs), Variational Autoencoders (VAEs), Diffusion Models [49] Medical imaging (OCT, MRI), time-series data, high-dimensional omics data [49] High fidelity requirements; computational intensity; privacy preservation
Statistical & Probabilistic Bayesian networks, sampling techniques [47] Tabular clinical trial data, electronic health records (EHRs) Handles structured data well; may struggle with complex correlations
Hybrid Approaches ADS-GAN, PATE-GAN, Time-GAN [47] Multimodal data integration, longitudinal patient data Balances privacy and utility; specialized for temporal patterns

Synthetic data enables multiple critical applications: reducing clinical trial costs and duration (especially for rare diseases), enhancing AI predictive power in personalized medicine, ensuring fair treatment recommendations across diverse populations, and providing access to high-quality multimodal datasets without privacy concerns [49]. For example, synthetic data can generate thousands of variations of rare medical images under different conditions, improving defect detection accuracy from 70% to 95% in one documented case [48].

Transfer Learning and Ensemble Frameworks

Transfer learning leverages knowledge from data-rich source domains to boost performance in target domains with limited data. The ETSEF (Efficient Transfer and Self-supervised Learning based Ensemble Framework) represents a cutting-edge approach that strategically combines transfer learning, self-supervised learning, and ensemble learning [46].

ETSEF integrates features from multiple pre-trained models, uses multi-model feature fusion and decision voting, and has demonstrated up to 14.4% improvement in diagnostic accuracy compared to state-of-the-art methods across five independent medical imaging tasks including endoscopy, brain tumor detection, and glaucoma detection [46]. This framework maximizes feature representation power from limited samples while maintaining robustness through ensemble decision mechanisms.

G cluster_0 Phase 1: Knowledge Transfer cluster_1 Phase 2: Feature Learning cluster_2 Phase 3: Ensemble Decision Source Domains Source Domains Pre-trained Models Pre-trained Models Source Domains->Pre-trained Models Source Domains->Pre-trained Models Target Clinical Task Target Clinical Task Feature Extraction Feature Extraction Target Clinical Task->Feature Extraction Target Clinical Task->Feature Extraction Pre-trained Models->Feature Extraction Pre-trained Models->Feature Extraction Feature Fusion Feature Fusion Feature Extraction->Feature Fusion Feature Extraction->Feature Fusion Ensemble Voting Ensemble Voting Feature Fusion->Ensemble Voting Feature Fusion->Ensemble Voting Final Prediction Final Prediction Ensemble Voting->Final Prediction Ensemble Voting->Final Prediction

Prospective Active Learning for Clinical Trials

Traditional active learning assumes independent and identically distributed (i.i.d.) data, which doesn't reflect the temporal dependencies in clinical trials where treatment results create relationships between current and past visits [50]. Prospective active learning addresses this by conditioning sample selection on the temporal context of data collection.

This methodology is particularly valuable for disease detection in longitudinal imaging studies like optical coherence tomography (OCT), where it outperforms retrospective active learning approaches by accounting for the non-i.i.d. structure of clinical trial data [50]. The prospective framework more accurately simulates real-world clinical deployment where models encounter data sequentially rather than in batch.

Technical Approaches for Data Imbalance

Data-Level Balancing Techniques

Data-level methods directly adjust training set composition to balance class distributions. These approaches include oversampling the minority class, undersampling the majority class, or hybrid methods.

Table 2: Data-Level Methods for Handling Class Imbalance

Method Key Variants Mechanism Clinical Considerations
Oversampling Random Oversampling, SMOTE, K-Means SMOTE, SVM-SMOTE [51] Increases minority class representation through duplication or synthetic generation Risk of overfitting to repeated/synthetic patterns; simpler methods often match complex ones [52]
Undersampling Random Undersampling, Edited Nearest Neighbors, Tomek Links, Cluster-Based [51] Reduces majority class samples to balance distribution Potential loss of informative majority samples; computational intensity of cleaning methods [52]
Hybrid Methods SMOTE+ENN, ADASYN+Cluster Centroids [51] Combines oversampling and undersampling Can address both imbalance and noise; increased complexity
GAN-Based Conditional GANs, CycleGANs [51] Generates realistic synthetic minority samples High-dimensional capability; computationally demanding

Recent evidence suggests that with strong classifiers (XGBoost, CatBoost), simple random oversampling/undersampling often matches complex SMOTE variants when proper probability threshold tuning is employed [52]. For weak learners (decision trees, SVMs), data-level methods show more significant benefits.

Algorithm-Level and Model-Level Solutions

Algorithmic approaches modify learning procedures to emphasize minority class performance without altering dataset composition.

Weighted Loss Functions directly address class imbalance by assigning higher misclassification costs to minority classes. Class weights are typically set inversely proportional to class frequencies: ( wc = \frac{N}{nc} ), where ( N ) is total samples and ( nc ) is class count [51]. Focal Loss extends this by down-weighting easy-to-classify examples, focusing learning on challenging cases: ( L = -\alpha(1-pt)^{\gamma}\log(p_t) ), where ( \alpha ) balances class importance and ( \gamma ) focuses on hard examples [51].

Ensemble Methods provide particularly effective imbalance solutions. Bagging methods like Balanced Random Forests and EasyEnsemble create balanced bootstrap samples, while boosting approaches like SMOTEBoost and RUSBoost integrate sampling directly into the sequential learning process [51]. Modern gradient boosting implementations (XGBoost, LightGBM, CatBoost) support native class weighting, often eliminating need for external sampling [52].

Strategic Evaluation Metrics and Validation

Proper evaluation is crucial when assessing models trained on imbalanced clinical data. Standard accuracy metrics can be profoundly misleading, as a model predicting only the majority class can achieve high accuracy while being clinically useless.

Table 3: Evaluation Metrics for Imbalanced Clinical Datasets

Metric Category Specific Metrics Formula Clinical Interpretation
Threshold-Dependent Precision, Recall, F1-Score [51] ( \text{Precision} = \frac{TP}{TP+FP} ) ( \text{Recall} = \frac{TP}{TP+FN} ) ( F1 = 2\cdot\frac{\text{Precision}\cdot\text{Recall}}{\text{Precision}+\text{Recall}} ) Precision: Reliability of positive predictions. Recall: Ability to find all positive cases.
Threshold-Independent AUC-PR, ROC-AUC [51] Area Under Precision-Recall Curve, Area Under ROC Curve AUC-PR more informative than ROC-AUC for imbalance as it focuses on positive class
Comprehensive Metrics Matthews Correlation Coefficient, Cohen's Kappa [51] ( \text{MCC} = \frac{TP\cdot TN - FP\cdot FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}} ) Balanced measures considering all confusion matrix categories

Probability threshold tuning is essential—the default 0.5 threshold is often suboptimal for imbalanced problems. Optimizing thresholds for specific clinical objectives (maximizing recall for screening, precision for confirmatory testing) significantly improves model utility [52]. Stratified splitting maintains original class distributions in train/validation/test sets, preventing misleading performance estimates [51].

Experimental Protocols and Validation Frameworks

Robust Model Selection and Error Estimation

Proper experimental design is crucial to prevent overfitting during model development. Nested cross-validation provides unbiased performance estimation by separating model selection and evaluation [2]. The outer loop assesses generalization ability while inner loops perform hyperparameter tuning, preventing information leakage from test sets into training [2].

Protocols that conduct feature selection on entire datasets before train/test splitting create significant bias, yielding overoptimistic performance estimates [2]. This is particularly problematic in high-dimensional clinical data (genomics, radiomics) where feature dimensionality vastly exceeds sample size.

G cluster_0 Outer Loop: Performance Estimation cluster_1 Inner Loop: Model Selection Full Dataset Full Dataset Training Fold 1 Training Fold 1 Full Dataset->Training Fold 1 Training Fold 2 Training Fold 2 Full Dataset->Training Fold 2 Training Fold K Training Fold K Full Dataset->Training Fold K Validation Fold 1 Validation Fold 1 Full Dataset->Validation Fold 1 Validation Fold 2 Validation Fold 2 Full Dataset->Validation Fold 2 Validation Fold K Validation Fold K Full Dataset->Validation Fold K Hyperparameter Tuning Hyperparameter Tuning Training Fold 1->Hyperparameter Tuning Training Fold 2->Hyperparameter Tuning Training Fold K->Hyperparameter Tuning Validation Fold 1->Hyperparameter Tuning Validation Fold 2->Hyperparameter Tuning Validation Fold K->Hyperparameter Tuning Model Selection Model Selection Hyperparameter Tuning->Model Selection Final Performance Estimate Final Performance Estimate Model Selection->Final Performance Estimate

Regularization and Model Complexity Control

Regularization techniques directly address overfitting by constraining model complexity. L1 (Lasso) and L2 (Ridge) regularization add penalty terms to loss functions, discouraging over-reliance on specific features [11]. For neural networks, dropout randomly deactivates neurons during training, preventing co-adaptation and improving generalization [11].

The optimal regularization strength depends on the degree of data scarcity and imbalance—stronger regularization is needed with smaller, noisier datasets. Automated hyperparameter optimization using Bayesian methods or genetic algorithms can efficiently navigate this complex tradeoff space.

The Scientist's Toolkit: Research Reagent Solutions

Table 4: Essential Tools for Addressing Data Scarcity and Imbalance

Tool/Category Specific Implementations Function and Utility Key Considerations
Synthetic Data Generation GANs, VAEs, Diffusion Models [49] Creates privacy-preserving artificial data mimicking real clinical distributions Python-dominated ecosystem (75.3%); requires significant validation [49]
Data Resampling Imbalanced-Learn, scikit-learn [52] Implements oversampling, undersampling, and hybrid methods Start with simple random sampling before advanced methods [52]
Ensemble Frameworks ETSEF, Balanced Random Forests, EasyEnsemble [46] [51] Combines multiple models to reduce variance and bias Demonstrated 13.3% improvement over ensemble baselines [46]
Gradient Boosting XGBoost, LightGBM, CatBoost [52] Strong classifiers with native class weighting Often reduces need for external sampling methods [52]
Model Interpretation Grad-CAM, SHAP, t-SNE [46] Explains model predictions and reveals decision boundaries Critical for clinical validation and trust building
Evaluation Metrics AUC-PR, F1-Score, MCC [51] Provides accurate performance assessment for imbalanced data Prevents misleading accuracy metrics

Addressing data scarcity and imbalance requires a systematic approach combining data, algorithmic, and evaluation strategies. For clinical researchers, we recommend: (1) beginning with strong classifiers (XGBoost, CatBoost) with class weights and proper threshold tuning before exploring complex sampling; (2) utilizing synthetic data for privacy-sensitive scenarios and rare cases; (3) implementing robust nested validation to prevent overfitting; and (4) selecting evaluation metrics aligned with clinical priorities.

The optimal solution typically combines multiple approaches—for instance, ETSEF's integration of transfer learning and ensemble methods [46] or hybrid sampling that both generates minority samples and cleans majority class noise [51]. By systematically addressing these data challenges through the technical frameworks presented here, clinical researchers can develop models that achieve the optimal balance between underfitting and overfitting, delivering reliable performance in real-world healthcare applications.

Model-Informed Drug Development (MIDD) leverages quantitative methods to accelerate hypothesis testing, assess drug candidates more efficiently, and reduce costly late-stage failures [32]. Machine learning (ML) and artificial intelligence (AI) are now central to this paradigm, transforming key stages of the pharmaceutical pipeline. However, the effectiveness of these computational models is critically dependent on their ability to generalize beyond their training data. The twin challenges of overfitting (where a model learns noise and specific patterns from the training data, leading to poor performance on new data) and underfitting (where a model is too simple to capture the underlying trends in the data) pose significant risks to the reliability of predictions in drug development [53] [54]. This guide provides an in-depth technical examination of three critical application areas—First-in-Human (FIH) dose prediction, ADME property forecasting, and clinical trial simulation—within the context of managing overfitting and underfitting to ensure robust, actionable outcomes.

Core Concepts: Overfitting and Underfitting in ML for Drug Development

In the context of pharmaceutical research, the pitfalls of overfitting and underfitting are not merely academic; they can lead to costly clinical failures or unsafe patient outcomes.

  • Overfitting occurs when a model is excessively complex, learning not only the underlying relationship in the training data but also the random noise and specific idiosyncrasies. An overfit model will exhibit excellent performance on the data it was trained on but will fail to generalize to new, unseen datasets (e.g., a different chemical library or a new patient population). Common causes include a model with too many parameters relative to the number of data points, or training for too many epochs [53] [54].
  • Underfitting is the opposite problem, where a model is too simplistic to capture the fundamental patterns in the data. An underfit model will perform poorly on both the training data and any new data, as it has failed to learn the true relationship between the input features and the target variable [54].

Techniques to mitigate these issues are essential for building trustworthy models. These include cross-validation, expanding the training set, curating predictive features, regularisation, and using ensemble methods [53]. Rigorous validation on independent external datasets is a non-negotiable step to ensure model stability and generalizability before deployment in a regulatory-sensitive environment [53].

FIH Dose Prediction

The primary goal of FIH dose prediction is to determine a safe starting dose and subsequent escalation scheme for initial human trials based on preclinical data. Accurate prediction is paramount for patient safety.

Methodological Approaches

A "fit-for-purpose" strategy is recommended, selecting the modeling approach based on the available data and the complexity of the drug's mechanism [32].

  • Mechanistic PBPK Modeling: For small molecules, Physiologically Based Pharmacokinetic (PBPK) modeling incorporates mechanistic understanding of physiology and drug properties. It uses physiochemical, in vitro, and preclinical in vivo data to simulate human pharmacokinetics (PK), accounting for factors like disease status and potential drug-drug interactions [32] [55].
  • Quantitative Systems Pharmacology (QSP): For complex biologics such as monoclonal antibodies, QSP models integrate preclinical mechanistic evidence and physiological system models to handle complexities like target-mediated drug disposition (TMDD) and immunogenicity [32] [55].
  • AI-Enhanced Forecasting: Machine learning algorithms, including deep learning and Generative Adversarial Networks (GANs), can analyze vast chemical and biological datasets to predict the biological activity and PK properties of novel compounds, accelerating the hit-to-lead optimization process [53].

Experimental Protocol for a Hybrid PBPK/ML Workflow

  • Data Acquisition and Curation: Collect high-quality in vitro data (e.g., permeability, metabolic stability, plasma protein binding) and in vivo PK data from animal models. Rigorous data cleaning is essential to remove noise and inaccuracies that can lead to model bias [53] [55].
  • Feature Selection: Identify the most relevant molecular descriptors and physicochemical properties (e.g., logP, molecular weight) as inputs for the model. This helps prevent overfitting by reducing unnecessary dimensionality [53].
  • Model Training with Cross-Validation:
    • Split the curated preclinical data into training and test sets.
    • Train a PBPK model or an ML algorithm (e.g., a neural network) on the training set to learn the relationship between input parameters and PK outcomes.
    • Use k-fold cross-validation on the training set to tune hyperparameters and select the optimal model complexity, thereby minimizing the risk of overfitting or underfitting [53].
  • External Validation and FIH Dose Projection:
    • Validate the final model's performance on a held-out test set that was not used during training or validation.
    • Use the validated model to simulate human PK profiles and predict a safe FIH dose. The starting dose is often selected based on achieving a target exposure shown to be safe in animal studies [55].

Table 1: Key Data Requirements for FIH Dose Prediction Models

Data Category Specific Parameters Use in Model
Physicochemical Properties Lipophilicity (LogP), pKa, solubility, molecular weight Input for PBPK and QSAR models to define drug characteristics [32] [53]
In Vitro Data Metabolic stability in liver microsomes, permeability (Caco-2), plasma protein binding To scale and predict human clearance, absorption, and free drug concentration [55]
In Vivo Preclinical PK Clearance, volume of distribution, half-life from animal studies For allometric scaling and model calibration [55]
Target Biology Affinity (KD), receptor occupancy, expression levels Critical for QSP and biologics models to predict pharmacodynamics (PD) and TMDD [55]

Workflow Diagram

fih_workflow start Preclinical Data Input data_curation Data Curation & Feature Selection start->data_curation model_training Model Training & Cross-Validation data_curation->model_training validation External Validation (Test Set) model_training->validation prediction FIH Dose Projection validation->prediction risk_overfit Risk: Overfitting risk_overfit->model_training Mitigation: Regularization risk_underfit Risk: Underfitting risk_underfit->model_training Mitigation: Increase Model Complexity

ADME Property Forecasting

Predicting Absorption, Distribution, Metabolism, and Excretion (ADME) properties is crucial for selecting promising drug candidates and optimizing lead compounds.

Methodological Approaches

  • Quantitative Structure-Activity Relationship (QSAR): A foundational computational method that uses molecular descriptors to predict the biological activity of compounds based on their chemical structure [32] [53]. The principle is that similar structures exhibit similar activities.
  • AI and Deep Learning: ML algorithms can analyze large-scale biomedical datasets to uncover hidden relationships between chemical structures and ADME endpoints. Deep learning models and GANs can generate novel molecular structures with optimized ADME and safety profiles [53].
  • PBPK Integration: As with FIH prediction, PBPK models provide a mechanistic framework to integrate in vitro ADME data for predicting overall PK behavior in humans [32].

Experimental Protocol for a QSAR/ML Model

  • Data Collection and Cleaning: Assemble a large, diverse dataset of chemical structures and their corresponding experimentally measured ADME properties. Inspect and correct for noise, inaccurate entries, and missing values. This step is critical, as model quality directly depends on data quality [53].
  • Molecular Featurization: Calculate molecular descriptors (e.g., molecular weight, electronegativity, hydrophobicity) or generate molecular fingerprints that numerically represent the chemical structures [53].
  • Model Training and Validation:
    • Split the dataset into training, validation, and test sets.
    • Train an ML model (e.g., random forest, neural network) on the training set.
    • Use the validation set for hyperparameter tuning and to monitor for overfitting. Techniques like early stopping can be employed.
    • Evaluate the final model's performance on the held-out test set using metrics like Area Under the Receiver Operator Curve (AUROC) or the Area Under the Precision-Recall Curve (AUPRC), the latter being more informative for imbalanced datasets [53].
  • External Validation and Deployment: Test the model on a completely independent external dataset to ensure generalizability before deploying it for virtual screening or lead optimization [53].

Table 2: Common ADME Endpoints and Predictive Modeling Features

ADME Property Experimental Measure Common Predictive Features (Molecular Descriptors)
Absorption Caco-2 permeability, Human intestinal absorption (%) Hydrogen bond donors/acceptors, Polar Surface Area (PSA), LogP [53]
Distribution Volume of Distribution (Vd), Plasma Protein Binding (%) LogP, pKa, Molecular Weight [32]
Metabolism Metabolic stability (e.g., half-life in microsomes), CYP enzyme inhibition Presence of specific metabolic substructures, Molecular fingerprints [53]
Excretion Fraction excreted unchanged in urine Molecular Weight, LogP, Rotatable bonds [32]

Workflow Diagram

adme_workflow start Chemical & ADME Database featurization Molecular Featurization start->featurization split Data Splitting (Train/Validation/Test) featurization->split training Model Training & Hyperparameter Tuning split->training testing Final Test & External Validation training->testing deploy Deploy for Virtual Screening testing->deploy overfit_alert High Performance on Training, Poor on Test overfit_alert->testing Indicates Overfitting

Clinical Trial Simulation

Clinical trial simulation uses mathematical and computational models to virtually predict trial outcomes, optimize study designs, and explore clinical scenarios before conducting actual trials, thereby increasing the probability of success [32].

Methodological Approaches

  • Population PK/PD (PopPK/PD) and Exposure-Response (ER): These models characterize the time course of drug exposure and its relationship to efficacy and safety outcomes, while accounting for variability between individuals. They are fundamental for informing dose selection and trial design [32].
  • Model-Based Meta-Analysis (MBMA): Integrates and quantitatively analyzes data from multiple clinical trials (both public and private) to understand the competitive landscape and define clinically relevant endpoints and effect sizes for a new trial [32].
  • Virtual Population Simulation: Creates diverse, realistic virtual patient cohorts to predict and analyze outcomes under varying conditions and trial designs [32].
  • Adaptive Trial Design: A model-based approach that uses accumulated "real-time" data to dynamically modify trial parameters, such as randomization ratios, making trials more efficient and ethical [32].

Experimental Protocol for a Simulation-Informed Trial Design

  • Define Objective and Endpoints: Clearly state the primary clinical question and the endpoints to be modeled (e.g., change in disease score, incidence of adverse event).
  • Develop a Base Model: Build a PopPK/PD or ER model using existing data (from earlier phases or literature). This model should describe the typical response and the key sources of inter-individual variability (IIV) [32].
  • Create Virtual Patients: Generate a virtual population that reflects the target patient demographic, disease status, and potential comorbidities. The size of this population should be large enough to achieve statistical power [32].
  • Simulate Trial Scenarios:
    • Run thousands of virtual trials under different design options (e.g., different doses, dosing regimens, sample sizes, inclusion/exclusion criteria).
    • Incorporate realistic assumptions about patient dropout, protocol deviations, and measurement error.
  • Analyze Simulation Output and Optimize:
    • Analyze the simulation outputs to estimate the probability of success (power) for each design scenario.
    • Identify the design that provides the best balance between high power, cost, and ethical considerations. This optimized design is then used for the actual clinical trial protocol.

Table 3: Key Inputs and Outputs for Clinical Trial Simulation

Input Category Specific Data Inputs Simulation Outputs & Decisions
Drug-Disease Model Placebo response, disease progression model, drug effect model (from preclinical/Phase II) Probability of trial success (power), Go/No-Go decisions [32]
Population Variability Demographics (weight, age), organ function, biomarker levels, genetic polymorphisms Understanding of key covariates, optimized inclusion/exclusion criteria [32]
Trial Design Parameters Number of patients, number of sites, treatment arms, dose levels, visit schedule, endpoint measurement times Optimal sample size, dose selection, and study duration [32]
Operational Factors Projected recruitment rate, dropout rates, protocol compliance assumptions Feasibility assessment, risk mitigation strategies [32]

Workflow Diagram

cts_workflow start Prior Knowledge (PhII, Literature, MBMA) base_model Develop Base PK/PD Model start->base_model virtual_pop Generate Virtual Patient Population base_model->virtual_pop simulate Simulate Multiple Trial Scenarios virtual_pop->simulate analyze Analyze Power & Optimize Design simulate->analyze final_design Finalized Trial Protocol analyze->final_design underfit_alert Model Fails to Capture Key Covariates underfit_alert->base_model Leads to Underfitting

The Scientist's Toolkit: Essential Research Reagents & Solutions

Table 4: Key Computational Tools and Platforms

Tool/Platform Name Type Primary Function in Application Spotlight
Simcyp Simulator [55] PBPK Software Platform Industry-standard for mechanistic FIH PK prediction and DDI risk assessment for small molecules and biologics.
ProgressiVis [56] Python Toolkit Enables building Progressive Visual Analytics (PVA) systems for scalable, interactive exploration of large-scale clinical and omics data.
TTK (Topology ToolKit) [56] Library for Topological Data Analysis Used for analyzing and visualizing complex scientific data from simulations (e.g., clinical trial outputs) based on topological relationships.
QSAR Modeling Software (e.g., RDKit, MOE) Cheminformatics Toolkits Provides environments and algorithms for calculating molecular descriptors and building robust QSAR models for ADME prediction.
PopPK/PD Software (e.g., NONMEM, Monolix) Pharmacometric Tools The gold-standard for developing population models that form the core of clinical trial simulations and exposure-response analysis.
Generative Adversarial Networks (GANs) [53] Deep Learning Architecture Used for de novo molecular design, generating novel chemical structures with optimized ADME and potency profiles.

In the development of machine learning (ML) models for high-stakes fields like drug development and healthcare, the pursuit of model generalization is not merely a technical objective but a fundamental regulatory requirement. Overfitting and underfitting represent two poles of a critical challenge: creating models that are both sufficiently accurate and reliably generalizable for regulatory approval and real-world application. An overfitted model learns not only the underlying patterns in the training data but also the noise and irrelevant details, resulting in exceptional performance on training data but failure to generalize to new, unseen data [57] [2]. Conversely, an underfitted model is too simplistic and fails to capture the underlying trends in the training data, resulting in poor performance on both training and test datasets [57] [1]. For regulatory agencies, the core concern is whether a model will perform safely and effectively when deployed in real-world clinical settings, making the management of overfitting and underfitting a cornerstone of compliant ML development [58].

The regulatory landscape for AI/ML in healthcare is rapidly evolving. Regulatory Agencies (RAs) emphasize that models must demonstrate technical robustness and safety in relation to the data used and the level of evidence generated [58]. The use of ML in clinical trials—from patient recruitment to study design and endpoint definition—impacts RA activities and necessitates a standardized approach to assessment [58]. This guide provides a comprehensive framework for researchers and drug development professionals to build fit-for-purpose models that navigate these complex requirements, ensuring that models are not only statistically sound but also regulatorily compliant.

Core Concepts: Overfitting, Underfitting, and the Bias-Variance Tradeoff

The performance and generalizability of a machine learning model are governed by the bias-variance tradeoff, a fundamental concept that directly impacts a model's regulatory acceptability [1].

  • High Bias (Underfitting): The model is too simple and makes strong assumptions about the data, leading to high errors on both training and test data. It fails to learn the relevant patterns [1].
  • High Variance (Overfitting): The model is too complex and is highly sensitive to the training data, leading to low training error but high test error. It has essentially memorized the training set, including its noise [1].

The goal is to find the optimal balance—a model with enough complexity to capture the underlying patterns (low bias) but not so complex that it memorizes the noise (low variance). This is the point of a good fit, where the error on the test set is minimized, signaling strong generalizability [1]. The following table summarizes the key characteristics:

Table 1: Characteristics of Model Fit States

Feature Underfitting Overfitting Good Fit
Performance Poor on train & test [1] Great on train, poor on test [1] Good on train & test [1]
Model Complexity Too Simple [1] Too Complex [1] Balanced [1]
Bias & Variance High Bias, Low Variance [1] Low Bias, High Variance [1] Low Bias, Low Variance [1]
Analogy Knows only chapter titles [1] Memorized the whole book [1] Understands the concepts [1]
Regulatory Risk Model is ineffective; fails to detect true effects [58] Model is unreliable and unsafe; predictions fail in real-world [58] [2] Model is reliable and generalizable [58]

Regulatory Framework for ML in Clinical Trials and Drug Development

The integration of ML into clinical trials (CTs) introduces specific regulatory challenges. Regulatory Agencies (RAs) like the EMA and FDA are actively developing frameworks to assess these technologies, which may be used for patient recruitment, study design, or endpoint definition [58]. A key regulatory consideration is that ML software tools intended for therapeutic or diagnostic decision-making are likely to be regulated as medical devices under regulations such as the EU Medical Device Regulation (MDR) [58].

Assessment of ML tools in a CT setting focuses on several key areas to ensure trustworthiness. The most impacted areas are those related to technical robustness and safety of the ML tool, in relation to the data used and the level of evidence generated [58]. Additional areas of attention include data and algorithm transparency [58]. The following diagram illustrates the key pillars for regulatory assessment of an ML model in a clinical setting:

RegulatoryPillars Regulatory Assessment Regulatory Assessment Data Management &\nRobustness Data Management & Robustness Regulatory Assessment->Data Management &\nRobustness Algorithm\nTransparency Algorithm Transparency Regulatory Assessment->Algorithm\nTransparency Intended Use &\nClinical Setting Intended Use & Clinical Setting Regulatory Assessment->Intended Use &\nClinical Setting Output &\nEvidence Generation Output & Evidence Generation Regulatory Assessment->Output &\nEvidence Generation Data Standardization Data Standardization Data Management &\nRobustness->Data Standardization Bias Assessment Bias Assessment Data Management &\nRobustness->Bias Assessment Security Security Data Management &\nRobustness->Security Version Control Version Control Algorithm\nTransparency->Version Control Decision Rationale Decision Rationale Algorithm\nTransparency->Decision Rationale Comparison to\nExisting Tools Comparison to Existing Tools Algorithm\nTransparency->Comparison to\nExisting Tools Clinical Need Clinical Need Intended Use &\nClinical Setting->Clinical Need Benefit-Risk\nAssessment Benefit-Risk Assessment Intended Use &\nClinical Setting->Benefit-Risk\nAssessment Standards of Care Standards of Care Intended Use &\nClinical Setting->Standards of Care Endpoint Correlation Endpoint Correlation Output &\nEvidence Generation->Endpoint Correlation Validation &\nError Estimation Validation & Error Estimation Output &\nEvidence Generation->Validation &\nError Estimation

To support regulatory submissions, developers must be prepared to address key informational points, often categorized as follows [58]:

  • Data (DTA): A data management plan covering type, origin, acquisition method, reliability, security, standardization, potential biases, and management of low-quality data.
  • Algorithm (ALG): The type of result expected, algorithm version, and comparison with previous experiences and available tools.
  • Output (OTP): A definition of the model's output and its correlation to the CT's scope, objectives, and/or endpoints. For decision-support software, an explanation of how the algorithm makes decisions is expected.
  • Intended Use (INU): The purpose of the tool and its added value for patients, including a specific risk assessment demonstrating that the tool is safe and appropriate for its intended use.

Experimental Protocols for Model Validation and Regulatory Compliance

Rigorous experimental design is non-negotiable for demonstrating that a model is fit-for-purpose and mitigating overfitting. The following protocols are essential.

Data Splitting and Cross-Validation

A foundational practice is the strict separation of data into training, validation, and test sets. The training set is used to train the model, the validation set for tuning hyperparameters, and the test set is reserved for the final, unbiased evaluation of model performance [59]. K-fold cross-validation is a robust technique to assess generalizability. The dataset is split into K subsets (folds). The model is trained on K-1 folds and tested on the remaining fold. This process is repeated K times, with each fold serving as the test set once. The final performance is averaged across all K trials [57] [59]. This helps reduce overfitting and ensures the model performs well across different data subsets [59]. The workflow for a robust validation protocol is as follows:

ValidationWorkflow cluster_split Initial Data Split cluster_cv K-Fold Cross-Validation Loop Start Original Dataset TrainingSet Training Set Start->TrainingSet TestSet Locked Test Set Start->TestSet Holdout for final evaluation FoldSplit Split Training Set into K Folds TrainingSet->FoldSplit FinalEval Final Model Evaluation on Locked Test Set TestSet->FinalEval TrainValidate For each fold: Train on K-1 Folds Validate on 1 Fold FoldSplit->TrainValidate Performance Average Performance Across All Folds TrainValidate->Performance HyperparameterTuning Hyperparameter Tuning Based on CV Results Performance->HyperparameterTuning FinalModel Train Final Model on Entire Training Set HyperparameterTuning->FinalModel FinalModel->FinalEval

Error Estimation and Model Selection

The way error estimation is conducted can significantly bias the results. A classic demonstration in bioinformatics showed that with high-dimensional data, different protocols for combining feature selection and classification can lead to dramatically different error estimates [2]. The only unbiased protocol in a no-signal dataset was "full cross-validation" (also known as nested cross-validation), where feature selection is done exclusively on the training portion of the data [2]. In contrast, performing feature selection on the entire dataset before splitting ("partial cross-validation") introduces optimistic bias, while "biased resubstitution" (using the same data for training and testing) can yield a grossly misleading, perfect classification score [2]. This underscores the critical need for proper experimental design to generate trustworthy evidence for regulatory submissions.

The Scientist's Toolkit: Key Reagents for Robust ML Research

Building a compliant ML model requires a suite of methodological "reagents." The following table details essential components for developing and validating fit-for-purpose models.

Table 2: Research Reagent Solutions for Model Development and Validation

Tool Category Specific Examples Function & Purpose in Regulatory Context
Regularization Techniques L1 (Lasso), L2 (Ridge) Regularization [57] [1] Prevents overfitting by adding a penalty for model complexity. L1 can perform feature selection by shrinking coefficients to zero [1].
Model Validation Tools K-Fold Cross-Validation, Holdout Test Set [57] [59] Provides a robust estimate of model generalizability and prevents overfitting during model selection [59].
Performance Metrics Precision, Recall, F1 Score, AUC-ROC, Log Loss [59] Offers a nuanced view of model performance beyond accuracy, crucial for imbalanced datasets common in healthcare [59].
Bias & Fairness Audits Fairness Indicators, SHAP, LIME [60] [59] Detects and addresses discriminatory model behavior across protected classes, addressing ethical and regulatory requirements for fairness [60].
Data Management Data Management Plan, Stratified Sampling [58] [59] Ensures data reliability, standardization, and representative sampling, which is foundational for regulatory acceptance [58].

Advanced Validation: Monitoring and Addressing Model Decay in Production

Model validation does not end at deployment. For regulatory compliance and long-term efficacy, continuous monitoring is essential. Model performance can degrade over time as the underlying data distribution changes, a phenomenon known as data drift [59]. Continuous monitoring of the model's performance in production allows for the detection and addressing of these issues before they impact decision-making in clinical use [59].

A comprehensive monitoring framework should track:

  • Model Drift: Changes in the relationship between input and output data.
  • Performance Degradation: Drops in key performance metrics (e.g., precision, recall) on new, real-world data.
  • Anomalous Behavior: Unusual patterns in model predictions or inputs.

Establishing alerting systems and rollback mechanisms when confidence drops or KPIs degrade is a best practice for maintaining a model's regulatory standing and real-world utility [60] [59].

Navigating the regulatory landscape with machine learning models demands a disciplined, principled approach centered on managing overfitting and underfitting. A fit-for-purpose model is not simply the one with the highest training accuracy, but the one that achieves an optimal balance between bias and variance, demonstrated through rigorous, protocol-driven validation. By integrating strategies such as robust data splitting, cross-validation, regularization, and continuous monitoring, researchers and drug developers can build models that are not only scientifically sound but also meet the stringent requirements for safety, efficacy, and transparency demanded by global regulatory agencies. The path to successful regulatory approval is paved with evidence of a model's ability to generalize reliably beyond the data on which it was trained.

Diagnostic and Remediation Strategies for Model Failures

In machine learning, particularly in high-stakes fields like drug development, the ultimate goal is to build models that generalize—that perform reliably on new, unseen data. Overfitting and underfitting are two fundamental obstacles to this goal, representing opposite ends of a model's performance spectrum [1]. An overfit model, while potentially perfect on its training data, fails to generalize, rendering its predictions untrustworthy in real-world clinical or research settings. This guide provides researchers and scientists with the conceptual understanding and practical methodologies for detecting overfitting through the analysis of performance gaps and learning curves, framed within the critical context of developing robust, clinically meaningful models [61] [2].

Defining the Fit: Underfitting, Overfitting, and the Ideal Balance

The concepts of underfitting and overfitting are governed by the bias-variance tradeoff, a fundamental challenge in machine learning [1].

  • Underfitting (High Bias): Occurs when a model is too simple to capture the underlying patterns in the data. It fails to learn the relationships between input and output variables, resulting in poor performance on both the training and test data [1] [62]. It is characterized by high bias and low variance.
  • Overfitting (High Variance): Occurs when a model learns the training data too well, capturing not only the underlying patterns but also the noise and random fluctuations. It essentially "memorizes" the training set. The key indicator is a significant performance gap between the training and test sets [1] [63]. It is characterized by low bias and high variance.
  • Good Fit (Ideal Balance): A well-fitted model has enough complexity to capture the underlying patterns (low bias) but is not so complex that it memorizes the noise (low variance). This is the point where the error on the test set is at its minimum [1].

Table 1: Characteristics of Model Fit States

Feature Underfitting Overfitting Good Fit
Performance on Training Data Poor Excellent Good/Excellent
Performance on Test/Validation Data Poor Poor Good/Excellent
Model Complexity Too Simple Too Complex Balanced
Key Indicator High error on both sets Large performance gap Small performance gap
Analogy Knows only chapter titles Memorized the whole book Understands the concepts [1]

The Bias-Variance Decomposition

The journey from an underfitted to an overfitted model can be understood through the bias-variance decomposition of error [2]:

  • Training Data Error: The error of a model on the data used to derive it. This is typically an optimistic, downward-biased estimate of true generalization error.
  • True Generalization Error: The error of the model on the entire population or distribution from which the training data were sampled.
  • Estimated Generalization Error: The estimate of the true generalization error, obtained through robust procedures like a hold-out test set or cross-validation [2].

An overfitted model is one that accurately represents the training data but fails to generalize well to new data from the same distribution because some of the learned patterns are not representative of the population [2].

Detecting Overfitting via Performance Gaps

The most straightforward method for detecting overfitting is to identify a significant gap between a model's performance on the training data and its performance on a held-out validation or test set.

Core Methodology: Train-Validation-Test Split

A robust experimental protocol is essential for obtaining unbiased performance estimates [61].

  • Data Splitting: Implement a three-way data split to prevent information leakage and ensure a true estimate of generalization error.
    • Training Set (e.g., 80%): Used for model fitting and internal parameter learning.
    • Validation Set (e.g., 10%): Used for hyperparameter tuning, model selection, and early stopping.
    • Test Set (e.g., 10%): Held out for the final, unbiased evaluation of the selected model. It must be used only once, after all modeling decisions are finalized [61].
  • Performance Metric Selection: Choose metrics that align with the clinical or research objective. For classification, accuracy alone can be misleading; use a suite of metrics derived from the confusion matrix [30]:
    • Precision: The proportion of positive predictions that are correct. (Critical when the cost of false positives is high).
    • Recall (Sensitivity): The proportion of actual positives that are correctly identified. (Critical when the cost of false negatives is high).
    • F1-Score: The harmonic mean of precision and recall, useful when seeking a balance between the two [30].
    • Specificity: The proportion of actual negatives that are correctly identified.
  • Gap Analysis: Calculate the selected metrics for both the training and validation sets. A large gap (e.g., high training accuracy with significantly lower validation accuracy) is a primary indicator of overfitting [64] [65].

Case Study: The Perils of Data Leakage in Parkinson's Disease Detection

A 2025 study on ML for early Parkinson's Disease (PD) detection provides a cautionary tale. Researchers constructed two experimental pipelines [61]:

  • Pipeline A (Control): Included overt motor symptoms (e.g., tremor, rigidity), which are themselves diagnostic criteria.
  • Pipeline B (Subclinical Scenario): Excluded all overt motor symptoms to simulate a true early detection scenario.

Table 2: Performance Gaps in Parkinson's Disease Detection Experiment

Model Type Feature Set Reported F1-Score Specificity Clinical Interpretation
Various ML Models (Logistic Regression, Random Forest, XGBoost, etc.) With Overt Features High (>90%) High Performance artificially inflated by data leakage.
The Same ML Models Without Overt Features Superficially Acceptable Catastrophically Low (~0%) Models failed, misclassifying most healthy controls as PD.

The results demonstrated that the high accuracy in the first pipeline was due to data leakage—the models were learning from features that would not be available in a genuine early detection scenario. When these features were removed, the models failed catastrophically, a failure immediately apparent from the performance gap analysis, specifically the near-zero specificity [61]. This underscores the necessity of rigorous experimental design and clinically realistic feature selection.

Detecting Overfitting via Learning Curves

Learning curves are a powerful graphical tool for diagnosing model behavior over time or with varying data size [66].

Learning Curves Over Epochs (Iterations)

This type of curve is common in deep learning and iterative algorithms. It plots the model's performance metric (e.g., loss, accuracy) against the number of training epochs or iterations.

LearningCurvesOverEpochs cluster_1 X-Axis: Training Epochs/Iterations cluster_2 Y-Axis: Model Error (e.g., Loss) Title Learning Curves: Model Performance vs. Epochs XAxis Number of Epochs (Increasing ->) YAxis Error Value (Decreasing is better) IdealRegion Ideal Stopping Point (Minimum Validation Error) OverfittingRegion Overfitting Region TrainingCurve Training Error ValidationCurve Validation Error

Diagram 1: Learning curves show training and validation error over epochs. The point of minimum validation error is the ideal stopping point before overfitting begins.

The learning curve reveals the model's state [66] [64]:

  • Underfitting: Both training and validation error are high and converge at a high value. The model has not learned the underlying pattern.
  • Ideal Fit: Both training and validation error decrease and converge at a low value. The gap between them is small.
  • Overfitting: Training error continues to decrease, but validation error begins to increase after a certain point. The growing gap between the two curves is the hallmark of overfitting.

Learning Curves Over Model Complexity

Another perspective plots model performance against a hyperparameter that controls complexity, such as max_depth for a decision tree.

LearningCurvesOverComplexity cluster_1 X-Axis: Model Complexity (e.g., Tree Depth) cluster_2 Y-Axis: Model Error Title Learning Curves: Model Performance vs. Complexity XAxis Complexity (Increasing ->) YAxis Error Value UnderfittingRegion Underfitting Region (High Bias) IdealRegion Ideal Complexity OverfittingRegion Overfitting Region (High Variance) TrainingError Training Error ValidationError Validation Error

Diagram 2: As model complexity increases, training error consistently decreases, but validation error begins to rise after an optimal point, indicating overfitting.

In this view, underfitting occurs at low complexity, and overfitting occurs at high complexity, with the "sweet spot" located at the point where validation error is minimized [66] [65].

Experimental Protocol: Generating a Learning Curve

The following methodology, adapted from a California Housing dataset experiment, details how to generate a learning curve for a regression model [66]:

  • Data Preparation: Load and preprocess the data. Split into training and test sets, standardizing features if necessary.
  • Model Initialization: Select a model (e.g., Ridge Regression, Decision Tree) and initialize it.
  • Iterative Training and Evaluation: Train the model over a range of epochs or complexities. After each epoch/step:
    • Calculate Training Loss: Make predictions on the training set and calculate the loss (e.g., Root Mean Squared Error).
    • Calculate Validation Loss: Make predictions on the held-out validation set and calculate the loss.
    • Record Values: Store the training and validation losses for the current epoch.
  • Visualization: Plot the recorded losses against the epochs/complexity to create the learning curve.

The Researcher's Toolkit: Essential Reagents and Solutions

For researchers implementing these detection methods, the following "reagents" are essential for a robust experimental workflow.

Table 3: Essential Research Reagents for Overfitting Detection

Tool/Reagent Function/Purpose Example Implementation
K-Fold Cross-Validation A data resampling procedure to obtain a more reliable estimate of model performance than a single train-test split. It reduces the variance of the performance estimate. Split data into K folds (e.g., 5 or 10). Iteratively use K-1 folds for training and the remaining fold for validation. The final score is the average across all folds [63] [65].
Hold-Out Test Set A completely unseen dataset used for the final evaluation of the model's generalization ability after all development and tuning is complete. A one-time use dataset, typically 10-20% of the total data, that is locked away during model development [64].
Regularization (L1/L2) A technique that penalizes model complexity by adding a penalty term to the loss function. L1 (Lasso) can shrink coefficients to zero, performing feature selection. L2 (Ridge) shrinks coefficients uniformly. Add a penalty term (e.g., alpha * sum(coefficients^2) for L2) to the model's cost function to discourage over-reliance on any single feature [1] [65].
Early Stopping A callback method that halts the training process when the model's performance on the validation set stops improving, preventing it from overfitting to the training data. Monitor validation loss during training. Stop training when validation loss fails to improve for a specified number of epochs (patience) [1] [65].
Data Augmentation Artificially increasing the size and diversity of the training dataset by applying realistic transformations to existing data, helping the model learn more invariant features. In image analysis, apply rotations, flips, and crops. In other domains, introduce noise or synthetic sample generation [1] [63].

For researchers and scientists in drug development, detecting overfitting is not an academic exercise but a fundamental requirement for building trustworthy predictive models. By systematically analyzing performance gaps between training and validation sets and meticulously interpreting learning curves, practitioners can diagnose a model's failure modes. The experimental protocols and tools outlined in this guide—from rigorous data splitting and metric selection to cross-validation and regularization—provide a framework for identifying overfitting. This, in turn, is the first critical step towards mitigating it, ultimately leading to ML models that generalize reliably and can be safely translated into clinical practice.

In machine learning, particularly in high-stakes fields like drug development, the ability to create models that generalize well from training data to unseen data is paramount. This challenge is formally recognized as navigating the problems of overfitting and underfitting. While overfitting often receives significant attention for its tell-tale sign of a large performance gap between training and test data, underfitting represents a more fundamental failure: a model's inability to capture the underlying pattern in the data at all [41] [67]. This guide focuses on the identification and diagnosis of underfitting, a state where a model is too simplistic, leading to consistently poor performance on both training and validation datasets [41] [11]. For researchers and scientists, recognizing this failure mode is the critical first step in developing effective and reliable predictive models.

Core Concepts and Definitions

What is Underfitting?

Underfitting occurs when a machine learning model is too simple to capture the underlying trends or relationships within the dataset [4] [67]. An underfit model exhibits high bias, meaning it makes overly strong assumptions about the data, failing to learn its complexities [4] [68]. Imagine trying to model a complex, non-linear biological response using a simple linear function; the model's inherent rigidity would prevent it from accurately representing the phenomenon [4]. The consequence of underfitting is uniformly poor predictive performance, not just on new data, but even on the data it was trained on [41] [69]. It is a state of fundamental failure where the model has not learned the essential signal in the data [67].

Underfitting vs. Overfitting

Underfitting and overfitting represent two opposite ends of the model performance spectrum. The table below summarizes their key differences, which are crucial for accurate diagnosis.

Table 1: Contrasting Underfitting and Overfitting

Characteristic Underfitting Overfitting
Model Complexity Too simple [4] Too complex [41]
Pattern Captured Fails to capture the underlying pattern [41] Captures noise as if it were the pattern [41]
Performance on Training Data Poor [41] [11] Very high/Very low error [41] [11]
Performance on Validation/Test Data Poor [41] [11] Significantly worse than training data [41]
Analogy A student who didn't study for an exam [67] A student who memorized answers without understanding concepts [41]
Relationship to Bias & Variance High bias, Low variance [4] [68] Low bias, High variance [4] [68]

Quantitative Identification of Underfitting

The primary indicator of underfitting is consistently high error rates or low accuracy across all datasets—training, validation, and test [41] [11] [67]. Unlike overfitting, which is identified by a performance gap, underfitting is identified by a performance failure.

Key Performance Metrics for Diagnosis

A comprehensive evaluation using multiple metrics is essential to diagnose underfitting conclusively. The following table outlines the expected behavior of these metrics in an underfit model.

Table 2: Performance Metric Behavior in an Underfit Model

Model Type Metric Expected Behavior in Underfitting
Classification Accuracy Low on both training and validation sets [70]
Precision Low [59]
Recall (Sensitivity) Low [59]
F1-Score Low (due to low precision and recall) [59]
AUC-ROC Close to 0.5 (no discriminative power) [59]
Log Loss High [71]
Regression Mean Absolute Error (MAE) High [70]
Mean Squared Error (MSE) High [70]
R-squared (R²) Low (close to 0) [71]

The Experimental Protocol for Detection

A robust experimental workflow is required to reliably identify underfitting. The following diagram outlines the key steps in this diagnostic process.

Start Start Model Training Split Split Data: Train, Validation, Test Start->Split Train Train Model Split->Train EvalTrain Evaluate on Training Set Train->EvalTrain EvalVal Evaluate on Validation Set EvalTrain->EvalVal CheckPerf Check Performance EvalVal->CheckPerf Underfit Diagnosis: Underfitting CheckPerf->Underfit High error on both sets

Diagram 1: Experimental workflow for identifying underfitting

This workflow relies on a proper data splitting strategy. A common approach is to hold out a portion of the data as a final test set (e.g., 15-30%), using the remainder for training and a validation set for tuning and diagnosis [70]. For more robust evaluation, especially with limited data, k-fold cross-validation is recommended. This technique involves splitting the data into k subsets (folds), training the model on k-1 folds, and validating on the remaining fold, repeating this process k times [71] [70]. The performance is then averaged across all folds, providing a more reliable estimate of model behavior and making it easier to spot the consistent poor performance indicative of underfitting.

The Bias-Variance Tradeoff Framework

Understanding underfitting is impossible without the conceptual framework of the bias-variance tradeoff. This tradeoff is a central problem in supervised machine learning that describes the tension between a model's simplicity and its complexity [4] [11].

  • Bias: Error from erroneous assumptions in the learning algorithm. High-bias models are too simple and fail to capture important patterns, leading to underfitting [4] [69].
  • Variance: Error from sensitivity to small fluctuations in the training set. High-variance models are too complex and learn the noise in the data, leading to overfitting [4] [11].

An underfit model is characterized by high bias and low variance [4] [68]. It is simplistic and stable (low variance), but its predictions are systematically incorrect (high bias) because its rigid assumptions do not match the complexity of the real-world data [67]. The goal of model development is to find the optimal balance between bias and variance, minimizing both to achieve a model that generalizes well.

A Researcher's Toolkit for Addressing Underfitting

Once underfitting is diagnosed, researchers must take deliberate steps to increase the model's learning capacity. The following table details key strategies and their functions.

Table 3: Research Reagent Solutions for Mitigating Underfitting

Solution Function & Rationale
Increase Model Complexity Switch to a more powerful algorithm (e.g., from linear model to polynomial, decision tree, or neural network) to provide the model with the necessary capacity to represent complex patterns [41] [67].
Feature Engineering Create new, more informative input features or add relevant features that the model can use to learn the underlying relationships in the data [4] [11].
Reduce Regularization Weaken the constraints (e.g., L1/L2 regularization parameters) that were penalizing model complexity, thereby allowing the model more freedom to learn from the data [41] [69].
Increase Training Epochs/Duration Allow the model more time to learn by increasing the number of training epochs, especially for complex models like deep neural networks that require longer convergence times [41] [67].

Identifying underfitting through its signature of consistently poor performance metrics is a fundamental skill in machine learning research. It requires a disciplined approach involving rigorous evaluation on held-out datasets, a thorough analysis of multiple performance metrics, and an understanding of the bias-variance tradeoff. For researchers in drug development, where model reliability is critical, mastering this diagnostic process is the first step toward building robust predictive models. By systematically applying the experimental protocols and remediation strategies outlined in this guide, scientists can effectively navigate past the pitfall of underfitting and progress toward developing models that truly capture the complex patterns within their data.

In the pursuit of developing high-performing machine learning models, researchers and practitioners must navigate the fundamental challenge of the bias-variance tradeoff, which manifests most prominently as the dual threats of overfitting and underfitting [4] [11]. These phenomena represent opposite ends of the model performance spectrum and present significant obstacles to creating systems that generalize effectively to new, unseen data. Overfitting occurs when a model becomes too complex and learns not only the underlying patterns in the training data but also the noise and random fluctuations [72] [4]. This results in a model that performs exceptionally well on training data but fails to generalize to validation or test datasets—much like a student who memorizes textbook passages without understanding the underlying concepts [4] [1].

The consequences of overfitting are particularly acute in sensitive fields such as drug development and medical diagnostics, where model reliability can have profound implications. For instance, an overfitted medical diagnosis model might achieve near-perfect accuracy on training images but perform poorly on new patient scans because it has learned specific artifacts in the training data rather than general pathological features [11]. The architectural evolution toward deeper and more complex neural networks has exacerbated this challenge, making robust regularization strategies not merely beneficial but essential components of modern deep learning systems [73] [74].

This technical guide examines three fundamental techniques for mitigating overfitting: regularization, dropout, and data augmentation. Through a systematic analysis of their mechanisms, implementations, and experimental validations, we aim to provide researchers with a comprehensive framework for developing more robust and generalizable machine learning models, particularly in data-constrained environments common in scientific research and drug development.

Theoretical Foundation: Overfitting and Underfitting

Defining the Model Fit Spectrum

The performance of a machine learning model can be categorized into three primary states along a complexity spectrum:

  • Underfitting occurs when a model is too simple to capture the underlying patterns in the data [4] [11]. This results in poor performance on both training and testing datasets and is characterized by high bias and low variance [4] [1]. Common causes include oversimplified models, inadequate feature representation, insufficient training time, or excessive regularization [4] [75] [1]. For example, using linear regression to model a complex non-linear relationship will typically result in underfitting [11].

  • Appropriate Fitting represents the ideal balance where the model captures the essential patterns in the data without being overly influenced by noise [4]. Such a model has low bias and low variance, performing well on both training and unseen test data [1]. It demonstrates the optimal tradeoff between complexity and generalizability.

  • Overfitting occurs when a model becomes too complex relative to the amount and noisiness of the training data [65]. The model essentially "memorizes" the training dataset rather than learning generalizable patterns, resulting in low bias but high variance [4] [1]. This is exemplified by a decision tree that grows to its maximum depth, perfectly classifying all training samples but failing to generalize to new data [65].

The Bias-Variance Tradeoff

The relationship between bias and variance represents a fundamental tradeoff in machine learning [4] [11]. Bias refers to the error introduced by approximating a real-world problem with an oversimplified model, while variance measures the model's sensitivity to small fluctuations in the training dataset [4] [11]. Increasing model complexity typically reduces bias but increases variance, while decreasing complexity has the opposite effect [4]. The optimal balance is achieved when both bias and variance are minimized, resulting in the best generalization performance [4] [1].

Table 1: Characteristics of Model Fitting States

Characteristic Underfitting Appropriate Fitting Overfitting
Training Performance Poor Good Excellent
Testing Performance Poor Good Poor
Model Complexity Too low Balanced Too high
Bias High Low Low
Variance Low Low High
Primary Cause Oversimplification Optimal complexity Excessive complexity relative to data

Regularization Techniques

L1 and L2 Regularization

Regularization represents a foundational approach to preventing overfitting by adding a penalty term to the loss function, discouraging the model from assigning excessive importance to any single feature [72] [11]. The two most common forms are L1 and L2 regularization:

  • L1 Regularization (Lasso): Adds the absolute values of the weights as a penalty term to the loss function (L1 norm) [72] [11]. This approach encourages sparsity by driving some weights to exactly zero, effectively performing feature selection [72] [1]. It is particularly useful when dealing with high-dimensional data where feature selection is desirable.

  • L2 Regularization (Ridge): Adds the squared values of the weights as a penalty term to the loss function (L2 norm) [72] [11]. This technique tends to distribute weight more evenly across all features, reducing the magnitude of weights without typically driving them to zero [72] [1]. L2 regularization generally produces more stable solutions than L1.

The mathematical formulation for the regularized loss function is:

$L{regularized} = L{original} + \lambda \sum{i=1}^{n} |wi|$ (for L1)

$L{regularized} = L{original} + \lambda \sum{i=1}^{n} wi^2$ (for L2)

Where $L{original}$ is the original loss function, $\lambda$ is the regularization parameter controlling the penalty strength, and $wi$ are the model weights.

Experimental Protocol: Evaluating Regularization Effectiveness

A systematic evaluation of regularization techniques was conducted in a 2025 study comparing baseline CNNs and ResNet-18 architectures for image classification [73] [74]. The experimental protocol employed:

  • Datasets: Imagenette dataset at varying resolutions (160px, 320px, 480px) [74]
  • Model Architectures: Baseline CNN (4 convolutional layers, 2 fully connected layers) and ResNet-18 [74]
  • Training Protocol: 100 epochs with early stopping, batch size of 32, Adam optimizer [74]
  • Regularization Methods: Weight decay (L2 regularization) with λ=0.0001, dropout (p=0.3), data augmentation [74]
  • Evaluation Metrics: Training accuracy, validation accuracy, generalization gap (difference between training and validation accuracy) [74]

Table 2: Performance of Regularized Models on Image Classification Task

Model Architecture Regularization Strategy Training Accuracy (%) Validation Accuracy (%) Generalization Gap (%)
Baseline CNN None 85.42 63.58 21.84
Baseline CNN L2 + Dropout + Augmentation 75.16 68.74 6.42
ResNet-18 None 95.21 76.33 18.88
ResNet-18 L2 + Dropout + Augmentation 84.95 82.37 2.58

The results demonstrate that regularization techniques significantly reduce the generalization gap across both architectures, with ResNet-18 achieving superior overall performance [74]. The combination of architectural innovations (skip connections) with comprehensive regularization yielded the most robust performance, highlighting the synergistic relationship between model architecture and regularization strategies [74].

G Regularization Impact on Model Complexity cluster_0 Model Complexity Spectrum Underfitting Underfitting High Bias, Low Variance GoodFit Appropriate Fit Low Bias, Low Variance Underfitting->GoodFit Increases Complexity Overfitting Overfitting Low Bias, High Variance Overfitting->GoodFit Regularization L1 L1 Regularization (Lasso) L1->Overfitting Reduces L2 L2 Regularization (Ridge) L2->Overfitting Reduces

Dropout Regularization

Mechanism and Implementation

Dropout is a specialized regularization technique designed specifically for neural networks that operates by randomly deactivating a fraction of neurons during each training iteration [72] [75]. Introduced as a method to prevent complex co-adaptations between neurons, dropout effectively trains an ensemble of multiple "thinned" networks that share parameters [74]. The implementation involves:

  • Training Phase: For each training sample and at each iteration, each neuron (excluding those in the output layer) is temporarily "dropped out" with probability $p$, meaning it is omitted from the forward and backward passes [72] [74].
  • Testing Phase: All neurons are used, but their outputs are multiplied by $p$ to maintain appropriate expected values, or alternatively, using "inverted dropout" where activations are scaled by $1/p$ during training [74].

The dropout rate $p$ (the probability of retaining a neuron) is typically set to 0.5 for hidden layers and closer to 1.0 (e.g., 0.8) for input layers, though optimal values depend on the specific architecture and application [74].

Advanced Dropout Variants

The success of standard dropout has led to the development of several architectural variants designed to address specific challenges:

  • DropBlock: A structured form of dropout for convolutional networks where contiguous regions of feature maps are dropped rather than individual units [74]. This approach more effectively regularizes convolutional layers by accounting for spatial correlations [74].
  • Stochastic Depth: A technique for residual networks that randomly drops entire layers during training, effectively shortening the network and improving gradient flow [74]. This approach has shown particular effectiveness with ResNet architectures [74].

The interaction between dropout and batch normalization requires careful consideration, as their simultaneous use can sometimes lead to performance degradation due to conflicting behaviors during training [74].

Data Augmentation

Principles and Techniques

Data augmentation encompasses a series of techniques that generate high-quality artificial data by applying realistic transformations to existing data samples [76]. By artificially expanding the training dataset, data augmentation encourages models to learn more invariant representations and reduces reliance on spurious features [72] [76]. The core principle is to create modified versions of training examples that preserve the essential semantic content while introducing meaningful variations [76].

Data augmentation techniques vary significantly across data modalities:

  • Image Data: Rotation, translation, scaling, flipping, color space adjustments, cropping, and elastic deformations [72] [76]. Advanced approaches include style transfer and generative adversarial networks (GANs) [76].
  • Text Data: Synonym replacement, random insertion, random swap, random deletion, back-translation, and contextual embedding replacement [76].
  • Graph Data: Node dropping, edge perturbation, attribute masking, and subgraph sampling [76].
  • Tabular Data: Generative methods (GANs, VAEs) and statistical approaches (SMOTE) for addressing class imbalance [76].

Experimental Protocol: Data Augmentation for Medical Imaging

In drug development and medical research, data augmentation plays a critical role in addressing limited dataset sizes. A representative experimental protocol for medical image classification might include:

  • Baseline Dataset: 1,000 labeled medical images (e.g., tissue sections, radiographs) across 5 diagnostic categories
  • Augmentation Pipeline:
    • Geometric transformations: random rotation (±15°), horizontal flip (50% probability), random zoom (90-110%)
    • Color transformations: brightness adjustment (±20%), contrast variation (80-120%)
    • Advanced augmentations: elastic deformations, random erasing, mixup augmentation
  • Model Training: ResNet-50 architecture pre-trained on ImageNet, fine-tuned with SGD optimizer (learning rate=0.001, momentum=0.9)
  • Evaluation: 5-fold cross-validation with stratified sampling, comparing with and without augmentation

Studies have demonstrated that properly implemented data augmentation can improve model generalization by 5-15% in medical imaging tasks, effectively reducing the generalization gap by making models invariant to clinically irrelevant variations [76].

G Data Augmentation Workflow for Medical Imaging OriginalData Original Medical Images GeometricTransforms Geometric Transformations OriginalData->GeometricTransforms ColorTransforms Color Space Adjustments GeometricTransforms->ColorTransforms Rotation Rotation GeometricTransforms->Rotation Flipping Flipping GeometricTransforms->Flipping Zoom Zoom GeometricTransforms->Zoom AdvancedTransforms Advanced Transformations ColorTransforms->AdvancedTransforms Brightness Brightness ColorTransforms->Brightness Contrast Contrast ColorTransforms->Contrast AugmentedData Augmented Training Set AdvancedTransforms->AugmentedData Elastic Elastic Deform. AdvancedTransforms->Elastic Erasing Random Erase AdvancedTransforms->Erasing TrainedModel Robust Trained Model AugmentedData->TrainedModel

Integrated Experimental Framework

Comparative Analysis of Regularization Strategies

A comprehensive understanding of regularization requires evaluating how different techniques interact and complement each other. The previously mentioned 2025 study systematically compared regularization methods across architectures [74]:

Table 3: Regularization Technique Effectiveness Across Architectures

Regularization Technique Baseline CNN Impact ResNet-18 Impact Computational Overhead Implementation Complexity
L2 Regularization Moderate improvement (+3.2% val accuracy) Minor improvement (+1.5% val accuracy) Low Low
Dropout (p=0.3) Significant improvement (+5.1% val accuracy) Moderate improvement (+2.8% val accuracy) Low Low
Data Augmentation Major improvement (+6.8% val accuracy) Significant improvement (+4.2% val accuracy) Medium Medium
Combined Approach Maximum improvement (+9.4% val accuracy) Maximum improvement (+6.9% val accuracy) Medium High

The results indicate that while all regularization techniques improve generalization, their relative effectiveness varies by architecture [74]. Baseline CNNs benefit more substantially from explicit regularization techniques like dropout, while ResNet's inherent architectural advantages (skip connections, batch normalization) provide some built-in regularization benefits [74].

The Scientist's Toolkit: Research Reagent Solutions

Table 4: Essential Research Reagents for Regularization Experiments

Research Reagent Function Implementation Examples Typical Settings
L2 Regularizer Adds weight penalty to loss function to prevent overfitting weightdecay in PyTorch optimizers, kernelregularizer in Keras λ=0.0001-0.01
Dropout Layer Randomly sets activations to zero during training torch.nn.Dropout, tf.keras.layers.Dropout p=0.3-0.5 for hidden layers
Data Augmentation Pipeline Generates augmented training samples torchvision.transforms, tf.keras.preprocessing.image.ImageDataGenerator Rotation: ±15°, Zoom: 0.9-1.1x
Early Stopping Callback Monitors validation loss and stops training when performance degrades EarlyStopping in Keras, PyTorch callbacks patience=10-20 epochs
Learning Rate Scheduler Adjusts learning rate during training to improve convergence ReduceLROnPlateau, CosineAnnealingLR Factor=0.1-0.5, patience=5-10
Gradient Clipping Prevents exploding gradients in deep networks torch.nn.utils.clipgradnorm, tf.clipbyglobalnorm max_norm=1.0-5.0

The systematic application of regularization techniques—including L1/L2 regularization, dropout, and data augmentation—represents a critical strategy for addressing the pervasive challenge of overfitting in machine learning models. As demonstrated through controlled experiments, these methods significantly reduce the generalization gap across diverse architectures, with ResNet-18 achieving superior validation accuracy (82.37%) compared to baseline CNNs (68.74%) when comprehensive regularization is applied [74].

For researchers in drug development and scientific fields characterized by limited data availability, these regularization strategies offer practical pathways to more robust and generalizable models. The integration of multiple complementary approaches typically yields the best results, as different techniques address overfitting through distinct mechanisms: weight constraints (L1/L2), architectural stochasticity (dropout), and data diversity (augmentation).

Future research directions include developing more sophisticated regularization techniques specifically designed for novel architectures, exploring the interplay between regularization and transfer learning in resource-constrained environments, and creating automated regularization selection frameworks that dynamically adapt to dataset characteristics and training dynamics [74]. As machine learning continues to advance in scientific domains, the principled application of regularization will remain essential for building reliable, generalizable models that translate effectively from training environments to real-world applications.

Within the broader research on model fit in machine learning, underfitting represents a critical failure mode where a model is too simplistic to capture the underlying structure of the data. This issue stands in direct opposition to overfitting, where a model becomes overly complex and learns noise alongside patterns [77] [1]. For researchers and scientists in fields like drug development, where predictive model accuracy is paramount, underfitting manifests as consistently poor performance across both training and validation datasets, leading to unreliable predictions and insights [78] [79].

The core of the underfitting problem lies in the bias-variance tradeoff. Underfitted models exhibit high bias, meaning they make strong oversimplifying assumptions about the data, and low variance, meaning they are insensitive to small fluctuations in the training set [4] [1]. This tradeoff dictates that efforts to reduce bias (and thus underfitting) by increasing model complexity must be carefully managed to avoid increasing variance to the point of overfitting [77] [4]. This paper provides an in-depth examination of three principal technical strategies to remediate underfitting: strategic feature engineering, calibrated increases in model complexity, and the judicious reduction of regularization.

Diagnosing Underfitting: Symptoms and Detection

Accurate diagnosis is the first step in remediating underfitting. An underfitted model fails to establish the dominant relationship between input and output variables, leading to an unacceptably high error rate on both the training set and unseen data [78] [79]. The following table summarizes the key performance characteristics that differentiate underfitting from a well-fit or overfit model.

Table 1: Diagnostic Indicators of Model Fit Status

Aspect Underfitting Well-Fit Model Overfitting
Performance on Training Data Poor [1] [79] Good [79] Excellent/Very High [1] [79]
Performance on Test/Validation Data Poor [1] [79] Good [79] Poor [1] [79]
Model Complexity Too Simple [1] Balanced [1] Too Complex [1]
Bias-Variance Profile High Bias, Low Variance [4] [1] Balanced [4] Low Bias, High Variance [4] [1]
Primary Cause Model cannot capture data patterns [78] Optimal complexity for the data [77] Model memorizes noise in training data [77]

The most straightforward diagnostic method is the performance gap analysis. A model is likely underfitting when metrics like accuracy, F1-score (for classification), or R² (for regression) are low and comparable on both training and validation splits [79]. Visualization through learning curves is another powerful tool. For an underfit model, both the training and validation error curves will converge to a high value, indicating that further training with the current configuration is unlikely to yield improvements [79].

Core Strategies for Remediating Underfitting

Feature Engineering to Enhance Predictive Signals

A primary cause of underfitting is that the input features provided to the model lack the predictive power or expressive capacity to represent the underlying data relationships [1]. Feature engineering addresses this by creating new, more informative features from raw data.

Table 2: Feature Engineering Techniques to Combat Underfitting

Technique Methodology Experimental Protocol / Implementation
Polynomial Feature Creation Generating new features by raising existing features to a power (e.g., x², x³) to capture non-linear relationships [77]. Use libraries like scikit-learn PolynomialFeatures. Standard protocol involves creating polynomial terms up to a specified degree (e.g., degree=2 or 3) after standardizing the data to mitigate multicollinearity [80].
Feature Interactions Creating new features by multiplying or dividing existing features to model synergistic effects between variables [80]. Manually create interaction terms (e.g., feature_A * feature_B) or use automated methods. Critical to scale features first and validate that new interactions improve validation performance [80].
Binning / Bucketing Transforming continuous numerical features into categorical ranges to simplify complex patterns and reduce noise [80]. Use pandas cut or qcut functions. Experiment with different binning strategies (equal-width, equal-frequency) and assess impact on model performance through cross-validation [80].
Domain-Specific Feature Creation Leveraging expert knowledge to create features that represent known phenomena in the data [81]. In drug discovery, this could involve creating molecular descriptors from compound structures. Protocol requires close collaboration with domain experts and iterative validation [81].
Date/Time Decomposition Extracting constituent elements (hour, day of week, month) from timestamp data to reveal temporal patterns [80]. Use datetime libraries to decompose a single timestamp into multiple cyclic features. For seasons, map months to categories; for time-of-day, create 'morning', 'afternoon' buckets [80].

The following workflow diagram illustrates a systematic, iterative protocol for diagnosing underfitting and applying feature engineering solutions, while also considering adjustments to model complexity and regularization.

G Start Start: Suspected Underfitting Diagnose Diagnose Performance Start->Diagnose Decision1 Training & Test Performance Both Poor? Diagnose->Decision1 Decision1->Diagnose No FE Feature Engineering (Refer to Table 2) Decision1->FE Yes MC Increase Model Complexity (Refer to Section 3.2) FE->MC RR Reduce Regularization (Refer to Section 3.3) MC->RR Evaluate Evaluate on Validation Set RR->Evaluate Decision2 Underfitting Resolved? Evaluate->Decision2 Decision2->FE No Success Success: Proceed to Final Test Decision2->Success Yes

Increasing Model Complexity

When feature engineering alone is insufficient, the model architecture itself may be inadequate. Increasing model complexity provides the model with the necessary capacity to learn more intricate patterns from the data [82] [81].

For traditional machine learning models, this can involve switching from a linear model (e.g., Linear Regression) to a non-linear model (e.g., Polynomial Regression, Support Vector Machines with non-linear kernels) or ensemble methods (e.g., Random Forests, Gradient Boosting) [1] [79]. In deep learning, complexity is increased by adding more hidden layers, creating a deeper network, or adding more neurons (units) per layer, creating a wider network [82] [81]. This transforms the model from a shallow function approximator to a more powerful one capable of representing complex, hierarchical features.

The experimental protocol for this adjustment must be methodical. A standard approach is to start with a simple base model and incrementally add layers or neurons while meticulously monitoring the performance on a held-out validation set [81]. The goal is to find the point where validation error is minimized before it begins to increase again, which signals the onset of overfitting. As one source notes, "Increasing the duration of training [can help], but it is important to be cognizant of overtraining, and subsequently, overfitting" [78]. In some highly complex domains, it may be necessary to use an overparameterized model to fully prevent underfitting, though this requires careful management to avoid memorization on small datasets [81].

Reducing Regularization

Regularization techniques are explicitly designed to prevent overfitting by penalizing model complexity [77] [83]. Consequently, when applied too aggressively, they can be a direct cause of underfitting by overly constraining the model and preventing it from learning meaningful patterns in the data [78] [1].

The primary regularization parameters that researchers should adjust to mitigate underfitting include:

  • L1/L2 Regularization Strength (λ): The lambda hyperparameter controls the weight of the penalty term in the loss function. Reducing this value weakens the constraint, allowing model weights to take on larger values and capture stronger relationships [78] [41].
  • Dropout Rate: In neural networks, dropout randomly deactivates a fraction of neurons during training. A high dropout rate (e.g., 0.5) can force the network to be too simplistic. Reducing the rate (e.g., to 0.2 or 0.3) allows for more complex co-adaptations between neurons [83] [41].

The experimental protocol involves starting with the default or previously used regularization settings and systematically reducing their strength in a controlled manner, such as by halving the λ value or reducing the dropout rate by 0.1 per experiment [41]. Performance must be evaluated on a validation set after each adjustment. It is critical to view this as a fine-tuning process; the objective is to find the "sweet spot" where regularization is just strong enough to prevent overfitting but not so strong that it causes underfitting [78].

The Scientist's Toolkit: Research Reagent Solutions

The following table catalogues essential "research reagents" – in this context, key software tools and libraries – that are indispensable for implementing the experimental protocols described in this guide.

Table 3: Essential Research Reagents for Mitigating Underfitting

Reagent (Tool/Library) Function/Application Key Utility in Addressing Underfitting
scikit-learn A comprehensive machine learning library for Python. Provides implementations for feature engineering (e.g., PolynomialFeatures, OneHotEncoder), model complexity adjustment (e.g., various algorithms from linear models to ensembles), and regularization tuning (e.g., Ridge, Lasso CV) [80].
TensorFlow / Keras An open-source platform for building and training deep learning models. Enables incremental increases in model complexity by adding layers and neurons easily. Offers built-in regularization layers (Dropout) and regularizers (L1/L2) whose parameters can be easily adjusted [83].
pandas & NumPy Foundational Python libraries for data manipulation and numerical computation. Critical for data preprocessing, feature engineering, binning, and creating interaction terms before model training [80].
Matplotlib / Seaborn Python libraries for data visualization and plotting. Used to create learning curves and diagnostic plots that are essential for visually identifying underfitting and monitoring remediation efforts [79].
Hyperopt / Optuna Frameworks for automated hyperparameter optimization. Systematically searches the hyperparameter space (e.g., for optimal regularization strength, model architecture) to find the configuration that minimizes validation error, balancing underfitting and overfitting [81].

Successfully remediating underfitting is a deliberate process of calibrating model capacity to data complexity. The three core strategies—feature engineering, increasing model complexity, and reducing regularization—are not mutually exclusive but are most powerful when applied iteratively and in concert [77]. The iterative workflow presented in this guide provides a structured experimental protocol for researchers.

For scientists in drug development and other research fields, the reliability of predictive models is non-negotiable. A model that is blind to significant patterns in the data due to underfitting can lead to flawed conclusions and costly missteps. By systematically applying these diagnostic and remedial techniques, researchers can build models that truly understand the underlying phenomena of interest, thereby enabling more accurate predictions and robust scientific insights. The ultimate goal remains finding the optimal balance in the bias-variance tradeoff, creating a model that is neither too simple nor too complex, but "just right" for the task at hand [77] [1].

In machine learning, the fundamental challenge of model selection revolves around navigating the trade-off between bias and variance, manifesting as underfitting and overfitting. An overfit model, which memorizes the training data including its noise, fails to generalize to new, unseen data. Conversely, an underfit model, overly simplistic, fails to capture the underlying patterns in the training data itself [84] [85]. For researchers in high-stakes fields like drug development, where model predictions can influence critical decisions, achieving a balance is paramount. This whitepaper details two advanced, synergistic methodologies for optimizing model performance: hyperparameter tuning and ensemble methods. Hyperparameter tuning systematically searches for the optimal configuration of a model's learning algorithm, while ensemble methods combine multiple models to create a single, more robust predictor. Together, they provide a powerful framework for building reliable, accurate, and generalizable machine learning systems.

Hyperparameter Tuning: A Systematic Approach

Core Concepts and Definitions

Hyperparameters are configuration variables that govern the training process of a machine learning algorithm. Unlike model parameters (e.g., weights and biases in a neural network) that are learned from data, hyperparameters are set prior to the training phase [86] [87]. They control aspects such as the model's capacity, learning speed, and regularization. Common examples include the learning rate for gradient-based optimizers, the number of trees in a Random Forest, the kernel of a Support Vector Machine, and the number of layers in a neural network [88] [85]. The core objective of hyperparameter optimization is to find the combination that results in the model with the best performance on unseen data, thereby directly combating both overfitting and underfitting [89].

Optimization Techniques: From Grid Search to Bayesian Methods

Several strategies exist for navigating the hyperparameter search space, each with distinct advantages and computational trade-offs.

  • Grid Search: A brute-force method that exhaustively evaluates all possible combinations within a predefined set of hyperparameter values. While it is guaranteed to find the best combination within the grid, it becomes computationally prohibitive as the number of hyperparameters grows [88] [85].
  • Random Search: This method randomly samples combinations from a specified distribution over the hyperparameter space. It often finds good combinations much faster than Grid Search because it does not waste resources on unpromising regions of the search space [85].
  • Bayesian Optimization: A more advanced, sequential approach that builds a probabilistic model (a surrogate) of the function mapping hyperparameters to model performance. It uses this model to select the most promising hyperparameters to evaluate next, efficiently balancing exploration and exploitation. Studies consistently show that Bayesian optimization outperforms both Grid and Random Search in terms of both speed and the quality of the final configuration [90] [91]. Popular libraries implementing Bayesian optimization include Optuna, HyperOpt, and scikit-learn's BayesianOptimization [85].

Table 1: Comparison of Key Hyperparameter Optimization Techniques

Method Core Principle Advantages Disadvantages Best-Suited For
Grid Search [88] Exhaustive search over a defined grid Guaranteed to find best point in grid; simple to implement Computationally expensive; curse of dimensionality Small, well-understood hyperparameter spaces
Random Search [85] Random sampling from defined distributions More efficient than Grid Search; good for initial exploration No guarantee of optimality; can miss important regions Spaces with low effective dimensionality
Bayesian Optimization [90] [91] Sequential model-based optimization Highly sample-efficient; faster convergence to good values Higher complexity; overhead of model maintenance Expensive-to-evaluate models (e.g., deep learning)

Ensemble Methods: The Wisdom of Crowds

Theoretical Foundation

Ensemble learning is a paradigm that combines multiple machine learning models (called base learners) to produce a single, superior predictive model. The core principle is that a group of weak learners can come together to form a strong learner, improving generalization and reducing the risk of overfitting [92] [93]. This is effectively achieved by reducing variance (e.g., through bagging) or bias (e.g., through boosting), or by making the model more robust to errors from any single base estimator [92].

Key Ensemble Architectures

  • Voting & Averaging: Combines the predictions of multiple, diverse base models for the final prediction. In hard voting, the class that receives the majority of votes is selected. In soft voting, the class probabilities from each model are averaged, and the class with the highest average probability is chosen [92].
  • Bagging (Bootstrap Aggregating): Trains multiple instances of the same base algorithm on different random subsets of the training data (drawn with replacement). This reduces variance and helps mitigate overfitting. The classic example is the Random Forest algorithm, which uses decision trees as base learners and further randomizes the feature set for each split [92] [93].
  • Boosting: An iterative technique that trains base learners sequentially, with each new model focusing on the errors made by the previous ones. This primarily reduces bias. Modern gradient boosting frameworks like XGBoost, LightGBM, and CatBoost are highly effective and widely used. A study on project failure prediction found CatBoost to achieve the highest accuracy (94.02%) among several optimized models [92] [89].
  • Stacking: A more complex architecture that uses a meta-learner to combine the predictions of several base learners. The base models are trained on the original data, and their predictions are used as input features to train the meta-model. Research has shown that a stacking ensemble with Decision Trees, K-Nearest Neighbors, and Logistic Regression as base-learners and an SVM as a meta-learner can achieve high accuracy (93.73%) [92].

EnsembleMethods Ensemble Method Architectures cluster_bagging Bagging (Reduces Variance) cluster_boosting Boosting (Reduces Bias) cluster_stacking Stacking B1 Bootstrap Sample 1 M1 Base Model B1->M1 B2 Bootstrap Sample 2 M2 Base Model B2->M2 B3 Bootstrap Sample n M3 Base Model B3->M3 Avg1 Aggregation (e.g., Majority Vote) M1->Avg1 M2->Avg1 M3->Avg1 M4 Base Model 1 W2 Re-weighted Data (Focus on Errors) M4->W2 M5 Base Model 2 M6 Base Model n Avg2 Final Model M6->Avg2 Weighted Vote W1 Weighted Training Data W1->M4 W2->M5 S1 Base Model (e.g., DT) Meta Meta-Model (e.g., SVM) S1->Meta S2 Base Model (e.g., KNN) S2->Meta S3 Base Model (e.g., LR) S3->Meta Final Final Prediction Meta->Final

Table 2: Performance of Optimized Models in Project Failure Prediction [92]

Model Type Specific Model / Technique Key Tuning / Composition Details Reported Accuracy
Classical (Tuned) Support Vector Machine (SVM) Optimized with Grid Search 93.61%
Classical (Tuned) Decision Tree (DT) Optimized with Grid Search 93.60%
Classical (Tuned) K-Nearest Neighbors (KNN) Optimized with Grid Search 92.46%
Boosting CatBoost Optimized ensemble 94.02%
Stacking Stacking Ensemble Base: DT, KNN, LR; Meta: SVM 93.73%
Voting Soft Voting Ensemble Combination of DT, KNN, LR, CatBoost 93.21%

Synergistic Application: A Protocol for Robust Model Development

The true power of these techniques is realized when they are applied synergistically. A recommended protocol for a robust machine learning project is as follows:

  • Baseline Establishment: Begin by training and evaluating a set of diverse, untuned base models (e.g., Logistic Regression, Decision Tree, SVM, KNN) to establish a performance baseline [92].
  • Hyperparameter Tuning: Select a promising subset of base models and perform hyperparameter optimization. Bayesian optimization is generally preferred for its efficiency, but Grid or Random Search can be used for simpler models [90] [91]. The goal is to create a set of well-tuned, high-performing, and diverse models.
  • Ensemble Construction: Use the tuned models from the previous step as base learners to construct ensembles. Experiment with different ensemble strategies such as soft voting, bagging, and stacking [92] [93].
  • Final Evaluation & Analysis: Evaluate the final ensemble model on a held-out test set. Use explainability tools like SHAP to interpret the model's predictions and validate that its decision-making aligns with domain knowledge, which is critical in scientific fields [92].

The Scientist's Toolkit: Essential Research Reagents

For researchers aiming to implement these advanced optimization techniques, the following "research reagents" — software tools and libraries — are essential.

Table 3: Essential Software Tools for Advanced Optimization

Tool / Library Function Key Features / Use Case
scikit-learn [88] Machine Learning Library Provides implementations of GridSearchCV, RandomizedSearchCV, and numerous ensemble methods (Voting, Bagging, Stacking). The foundation for many ML projects.
Optuna [90] Hyperparameter Optimization Framework A modern, define-by-run API for Bayesian optimization. Features pruning of inefficient trials, making it highly efficient.
XGBoost / CatBoost [92] [89] Boosting Libraries Highly optimized implementations of gradient boosting. Often achieve state-of-the-art results on tabular data and include built-in regularization.
SHAP [92] Model Interpretability Library Explains the output of any ML model by computing Shapley values from game theory. Crucial for understanding model decisions in scientific research.

In the rigorous pursuit of reliable machine learning models for scientific discovery and drug development, managing overfitting and underfitting is non-negotiable. A systematic approach that leverages the strengths of both hyperparameter tuning and ensemble methods offers a robust path forward. By first refining individual models through advanced optimization techniques like Bayesian search and then aggregating their predictive power through ensemble architectures such as stacking and boosting, researchers can build models that are not only accurate but also generalizable and interpretable. This dual strategy represents a cornerstone of modern, production-ready machine learning.

Robust Validation Frameworks and Comparative Model Analysis

K-Fold Cross-Validation and Holdout Set Strategies

In machine learning research, the development of a predictive model is inherently a battle against two fundamental challenges: overfitting and underfitting. An overfit model, which has memorized the noise and specific patterns of its training data, fails to generalize to new information. Conversely, an underfit model, which has failed to capture the underlying trend, is ineffective from the outset. For researchers and drug development professionals, the stakes of this balance are exceptionally high. A model that appears accurate during training but fails on real-world, unseen data can lead to flawed scientific conclusions or, in a clinical context, significant patient risk. Therefore, robust validation strategies are not merely a technical step but a scientific imperative for ensuring model reliability and trustworthiness.

This whitepaper provides an in-depth technical examination of two cornerstone validation methodologies: the Holdout Set Strategy and K-Fold Cross-Validation. We will dissect their theoretical foundations, detailed experimental protocols, and appropriate applications, with a consistent focus on their role in diagnosing and preventing overfitting and underfitting within rigorous research environments.

Core Conceptual Frameworks

The Holdout Set Strategy

The holdout method is the most fundamental form of validation. It involves partitioning the available dataset D into two mutually exclusive subsets: a training set and a test set [94] [95].

  • Purpose and Workflow: The training set is used to fit the model's parameters, while the test set is held back entirely until the final evaluation. This provides an estimate of the model's performance on unseen data [95]. A typical split ratio is 70:30 or 80:20, though this can be adjusted based on dataset size [94].
  • Role in Combating Overfitting: The holdout method provides a crucial initial check for overfitting. A significant performance gap between the training set (high accuracy) and the test set (low accuracy) is a classic indicator that the model has overfitted to the training data [96].
K-Fold Cross-Validation

K-Fold Cross-Validation is a more sophisticated resampling technique designed to provide a more robust estimate of model performance by leveraging the entire dataset more effectively [97] [98].

  • Purpose and Workflow: The dataset D is randomly shuffled and partitioned into K subsets (folds) of approximately equal size. The model is then trained and evaluated K times. In each iteration i, fold i is used as the test set, and the remaining K-1 folds are combined to form the training set. The final performance metric is the average of the scores from all K iterations [97] [98].
  • Role in Combating Overfitting: By training and testing the model on different data subsets, K-Fold provides a more reliable picture of generalization error. It reduces the risk of a model's performance being artificially inflated or deflated by a single, fortunate (or unfortunate) random split of the data [98] [99]. High variance in the scores across the K folds can itself be an indicator of model instability or overfitting [96].

The following diagram illustrates the logical workflow and data flow for the K-Fold Cross-Validation process.

k_fold_workflow Start Start with Full Dataset (D) Shuffle Shuffle Dataset Randomly Start->Shuffle Split Split into K Equal Folds Shuffle->Split Loop For each of the K iterations: Split->Loop TrainSet Use K-1 Folds as Training Set Loop->TrainSet TrainModel Train Model on Training Set TrainSet->TrainModel TestSet Use 1 Fold as Test Set EvalModel Evaluate Model on Test Set TestSet->EvalModel TrainModel->TestSet StoreScore Store Performance Score EvalModel->StoreScore Check All iterations complete? StoreScore->Check Check->Loop No Average Calculate Average Performance Check->Average End Final Performance Estimate Average->End

Quantitative Comparison and Analysis

The theoretical advantages of K-Fold Cross-Validation manifest in more stable and reliable performance estimates. The following table summarizes a quantitative comparison from an experiment on the California Housing dataset, contrasting a single holdout validation against a 5-Fold Cross-Validation [98].

Table 1: Performance Comparison of Holdout vs. K-Fold Cross-Validation on the California Housing Dataset

Validation Method Key Characteristic Reported R² Score(s) Final Average R²
Holdout (Single Split) Performance dependent on a single random split. 0.6115 (with one random state) 0.6115
5-Fold Cross-Validation Performance evaluated across five different splits. Fold 1: 0.6115, Fold 2: 0.6426, Fold 3: 0.6383, Fold 4: 0.6655, Fold 5: 0.6057 0.6327

The data in Table 1 reveals two critical insights. First, the performance of a single holdout split is highly variable and can change significantly with different random seeds (as noted in [99]). Second, while one fold in the K-Fold process achieved a similar score to the holdout (0.6115), the average score across all folds was higher (0.6327), suggesting a better and more stable estimate of the model's true generalization capability [98].

The choice between holdout and K-Fold involves a trade-off between computational expense and the statistical reliability of the performance estimate. The following table outlines the core strategic differences to guide researchers in their selection.

Table 2: Strategic Decision Guide: Holdout vs. K-Fold Cross-Validation

Aspect Holdout Validation K-Fold Cross-Validation
Primary Use Case Initial, rapid prototyping; model evaluation with very large datasets [99] [95]. Robust model evaluation & selection; hyperparameter tuning; small to medium-sized datasets [97] [98].
Computational Cost Low (model is trained once) [99]. High (model is trained K times) [100] [97].
Bias of Estimate Can be high, especially if the test set is small or not representative [97]. Generally lower, as more data is used for training in each round [97].
Variance of Estimate High (sensitive to the specific data split) [99] [95]. Lower (averaging over multiple splits reduces variability) [97] [98].
Data Utilization Inefficient; a portion of data is never used for training [99]. Efficient; every data point is used for both training and testing exactly once [97] [98].

Experimental Protocols for Research

Protocol A: Implementing the Holdout Method for Model Evaluation

This protocol is designed for a straightforward evaluation of a model's performance.

  • Data Splitting: Randomly shuffle the dataset D and split it into two parts: a training set (e.g., 70-80%) and a test set (e.g., 20-30%) using a fixed random seed for reproducibility [94] [95]. In Python's scikit-learn, this is achieved with the train_test_split function.
  • Model Training: Train the chosen model (e.g., a DecisionTreeClassifier) exclusively on the training set [95].
  • Model Evaluation: Use the trained model to make predictions on the held-out test set. Calculate relevant performance metrics (e.g., Accuracy, R², Mean Squared Error) based on these predictions [94] [95].
  • Final Model Training: For deployment, it is common practice to retrain the final model on the entire dataset (D) to leverage all available data before releasing it for use on future unknown cases [94].
Protocol B: Implementing K-Fold Cross-Validation for Robust Estimation

This protocol is preferred for obtaining a reliable performance estimate and for model selection.

  • Configure K-Fold: Choose a value for K (common choices are 5 or 10 [97] [98]) and instantiate a KFold object in scikit-learn. Set shuffle=True to randomize the data before splitting and specify a random_state for reproducibility [98].
  • Cross-Validation Loop: Iterate over the splits provided by the KFold object. For each split:
    • Use the training indices to subset the data and train the model.
    • Use the test indices to subset the data and evaluate the model.
    • Record the performance score for that fold [98].
  • Performance Summarization: After completing all K iterations, calculate the mean and standard deviation of the recorded performance scores. The mean represents the model's expected performance, while the standard deviation indicates the stability of the model across different data subsets [97] [98].
Advanced Consideration: Multi-Source Data in Clinical Research

A critical caveat for researchers, particularly in clinical and drug development settings, involves the structure of data sources. A recent study on ECG classification demonstrated that standard K-Fold Cross-Validation can yield overoptimistic performance estimates when the goal is to generalize to data from entirely new sources (e.g., new hospitals or patient cohorts) [101].

  • Recommendation: If your dataset contains data from multiple sources (e.g., different clinical trials, hospitals, or experimental batches), a leave-source-out (LSO) cross-validation is more appropriate. In LSO, each unique source is left out as the test set in turn, while the model is trained on all other sources. This provides a more realistic and reliable estimate of how the model will perform when deployed in a new, unseen environment [101].

The Scientist's Toolkit: Essential Research Reagents

The following table details key software and methodological "reagents" required for implementing the validation strategies discussed in this guide.

Table 3: Essential Research Reagents for Model Validation

Tool / Reagent Function / Purpose Example in Python Scikit-Learn
Data Splitter (Holdout) Randomly partitions a dataset into training and test subsets for initial validation. sklearn.model_selection.train_test_split [94] [95]
Data Splitter (K-Fold) Generates the indices for K sequential training/test splits for cross-validation. sklearn.model_selection.KFold [97] [98]
Stratified Splitter Preserves the percentage of samples for each class in the splits, crucial for imbalanced datasets (e.g., disease vs. control). sklearn.model_selection.StratifiedKFold [96]
Performance Metrics Quantifies model performance using standardized statistical measures. sklearn.metrics (e.g., accuracy_score, r2_score, mean_squared_error) [98] [99]
Base Estimator/Model The core machine learning algorithm to be validated and compared. Any estimator (e.g., LinearRegression, DecisionTreeClassifier) [98] [95]

The choice between holdout and K-Fold Cross-Validation is not a matter of identifying a universally superior technique, but of selecting the right tool for the specific research context. The holdout method offers speed and simplicity, valuable for large datasets or initial prototyping. However, K-Fold Cross-Validation is generally the gold standard for model evaluation and selection, providing a more robust, data-efficient, and reliable estimate of generalization error, which is critical for mitigating overfitting.

For the research scientist, a disciplined validation strategy is non-negotiable. It is the foundation upon which trustworthy models are built. By rigorously applying these protocols and understanding their trade-offs, researchers in drug development and other high-stakes fields can ensure their predictive models are not only accurate on paper but also robust and generalizable in practice, thereby delivering truly actionable and reliable scientific insights.

Nested Cross-Validation for Unbiased Hyperparameter Tuning

The central challenge in machine learning is developing models that generalize effectively—performing well on new, unseen data rather than just on the information they were trained on. This challenge is fundamentally governed by the balance between overfitting and underfitting [1] [11].

  • Overfitting occurs when a model is too complex. It learns not only the underlying patterns in the training data but also the noise and random fluctuations. Think of a student who memorizes textbook exercises without understanding concepts, failing when exam questions are phrased differently [1] [11]. An overfit model exhibits low bias but high variance, leading to excellent performance on training data but poor performance on test data.
  • Underfitting occurs when a model is too simple to capture the underlying patterns in the data. This is akin to a student who only reads chapter titles and lacks depth to answer specific exam questions [1] [11]. An underfit model has high bias and low variance, resulting in suboptimal performance on both training and test datasets.

Hyperparameter tuning is a standard technique to optimize model performance and avoid underfitting. However, when the same data is used to both tune hyperparameters and evaluate the final model's performance, it introduces a significant risk of overfitting bias or selection bias [102] [103] [104]. The model's performance estimate becomes overly optimistic because knowledge of the test set has inadvertently leaked into the model selection process [104]. Nested cross-validation (Nested CV) is an advanced validation framework specifically designed to eliminate this bias, providing a reliable estimate of a model's generalization error in scenarios involving hyperparameter tuning, feature selection, or model selection [102].

Understanding Nested Cross-Validation

The Conceptual Framework

Nested cross-validation is a disciplined methodology that rigorously separates the model optimization process from the model evaluation process. It achieves this through a two-layer validation structure [102] [103]:

  • Inner Loop (Hyperparameter Optimization): This loop is responsible for finding the optimal hyperparameters for a given model. Using only a subset of the data provided by the outer loop (the inner training set), it performs a search (e.g., via Grid Search or Random Search) to identify the hyperparameter set that yields the best performance, typically evaluated using an inner validation set [102]. The crucial point is that this inner loop never sees the data reserved by the outer loop for final testing.
  • Outer Loop (Performance Evaluation): This loop provides an unbiased estimate of the model's generalization performance. It holds out a portion of the data as the test set. The model, configured with the optimal hyperparameters found by the inner loop, is trained on the remaining outer training data and then evaluated on the held-out test set. This process is repeated across multiple outer folds, and the results are aggregated [102].

This separation ensures the test data in the outer loop remains completely unseen during the tuning process, preventing data leakage and yielding a realistic performance estimate [102].

The Critical Workflow

The following diagram illustrates the step-by-step workflow of the nested cross-validation process, highlighting the interaction between the outer and inner loops.

NestedCV Start Start: Full Dataset OuterSplit Outer Loop: Split into K folds (e.g., K=5) Start->OuterSplit OuterIteration For each outer fold: OuterSplit->OuterIteration HoldOut Reserve one fold as the Outer Test Set OuterIteration->HoldOut OuterTrain Remaining (K-1) folds form the Outer Training Set OuterIteration->OuterTrain InnerSplit Inner Loop: Perform hyperparameter tuning on Outer Training Set using m-fold CV (e.g., m=3) OuterTrain->InnerSplit SelectBest Select optimal hyperparameters based on inner CV performance InnerSplit->SelectBest TrainFinalInner Train a model on the entire Outer Training Set using optimal hyperparameters SelectBest->TrainFinalInner Evaluate Evaluate the trained model on the held-out Outer Test Set TrainFinalInner->Evaluate Aggregate Aggregate performance metrics across all outer folds Evaluate->Aggregate Repeat for each outer fold

What Nested Cross-Validation Is Not

To avoid common misconceptions, it is essential to clarify the purpose of nested CV [102]:

  • It is not a machine learning algorithm. It is an evaluation framework, not a model like SVM or Random Forest.
  • It does not directly improve model accuracy. Instead, it provides a credible and unbiased estimation of that accuracy on unseen data.
  • It is computationally expensive. Due to its cost, it is primarily used in research, benchmarking, and model comparison rather than in production deployment pipelines where simpler validation methods may suffice.

Experimental Protocols and Methodologies

A Standardized Experimental Protocol

For researchers in fields like drug development, a rigorous and reproducible methodology is paramount. The following protocol details the implementation of nested CV.

Objective: To obtain an unbiased estimate of the generalization error for a machine learning model requiring hyperparameter tuning.

Materials:

  • A labeled dataset, partitioned into features (X) and target (y).
  • One or more machine learning algorithms (e.g., Support Vector Machine, Random Forest).
  • A defined hyperparameter search space for each algorithm.
  • Computing resources sufficient for k * n * k model fits (where k and n are the number of outer and inner folds, respectively).

Procedure:

  • Define the Cross-Validation Loops: Specify the number of folds for the outer loop (e.g., outer_cv = KFold(n_splits=5, shuffle=True, random_state=42)) and the inner loop (e.g., inner_cv = KFold(n_splits=3, shuffle=True, random_state=42)). Using 5 or 10 folds for the outer loop and 3 or 5 for the inner loop is common [103].
  • Initialize the Model and Hyperparameter Grid: Select the model and define the parameter grid to be explored (e.g., for an SVM: param_grid = {'C': [0.1, 1, 10], 'kernel': ['linear', 'rbf']}).
  • Configure the Inner Loop Search: Set up the hyperparameter search object (e.g., GridSearchCV), passing the model, parameter grid, and inner CV object. This object will handle the tuning within each outer training fold.
  • Execute the Outer Loop: Use a function like cross_val_score to perform the outer loop. This function will automatically, for each fold: a. Split the data into outer training and test sets. b. Pass the outer training set to the GridSearchCV object. c. The inner loop performs tuning on this outer training set and finds the best hyperparameters. d. A final model is trained on the entire outer training set with the best hyperparameters. e. This model is evaluated on the outer test set, and the score is stored.
  • Aggregate Results: Calculate the mean and standard deviation of the scores from all outer folds. This represents the unbiased estimate of the model's generalization performance.
Python Implementation Code

The following code demonstrates a concrete implementation of the above protocol using the Iris dataset and a Support Vector Classifier (SVC) [102].

Quantitative Comparison of Validation Techniques

The table below summarizes the key differences between standard validation methods and nested cross-validation, highlighting why nested CV is superior for unbiased estimation.

Table: Comparison of Model Validation Strategies

Validation Method Primary Use Case Risk of Optimism Bias Computational Cost Quality of Generalization Estimate
Simple Train/Test Split Initial model prototyping High Low Low (Varies with single split)
Standard k-Fold CV Robust performance estimation Low Moderate High
CV with Hyperparameter Tuning Model optimization Very High (if score used for selection) High Overly Optimistic [103] [104]
Nested Cross-Validation Unbiased evaluation of a tuned model Very Low [102] [103] Very High Realistic and Reliable [102]

The Scientist's Toolkit: Research Reagent Solutions

For machine learning researchers, the "reagents" are the software tools and algorithms that enable the construction and evaluation of predictive models. The following table details essential components for implementing nested cross-validation.

Table: Essential Research Reagents for Nested CV Experiments

Reagent / Tool Function / Purpose Example in Scikit-Learn
Hyperparameter Search Algorithms Automate the exploration of hyperparameter spaces to find optimal configurations. GridSearchCV, RandomizedSearchCV
Resampling Methods Split data into training and validation/test sets in a robust, statistically sound manner. KFold, StratifiedKFold
Performance Metrics Quantify model performance according to the research objective (e.g., accuracy, AUC). accuracy_score, f1_score, roc_auc_score
Base Estimators The core machine learning algorithms to be evaluated and compared. SVC, RandomForestClassifier, XGBoost
Model Evaluation Framework The higher-level function that orchestrates the outer loop of the validation process. cross_val_score

Discussion: Implications for Robust Machine Learning Research

The Computational Cost and its Justification

The most significant drawback of nested CV is its computational expense. The total number of model fits is k_outer * k_inner * n_parameter_combinations [103]. For a grid of 100 hyperparameter combinations with 10 outer and 5 inner folds, this requires 5,000 model fits—a tenfold increase over a non-nested tuning procedure. However, this cost is not frivolous; it is the necessary price for a statistically rigorous and unbiased performance estimate. In high-stakes fields like drug development, where model generalizability is paramount, this investment is justified.

Configuring the Final Production Model

A common point of confusion is how to transition from the nested CV evaluation to a final deployable model. The procedure is as follows [103]:

  • Use the results from the outer loop of the nested CV to select the best algorithm.
  • Apply the inner loop procedure (hyperparameter tuning) to the entire dataset to find the single best set of hyperparameters for that algorithm.
  • Train a final model on the entire dataset using these optimal hyperparameters. This final model is what would be deployed or used for further predictions, and its expected performance is accurately reflected by the score from the nested CV procedure.
Advanced Considerations: Model Selection as a Hyperparameter

Nested cross-validation naturally extends to the problem of model selection. Different algorithm types (e.g., Random Forest vs. SVM) can be treated as a top-level hyperparameter [105]. The inner loop is then responsible for tuning the hyperparameters for each model family and selecting the best overall model configuration. This integrated approach prevents the optimistic bias that arises when model families are selected based on the same data used for their tuning and evaluation [106] [105].

Nested cross-validation is an indispensable methodology in the machine learning researcher's arsenal, particularly when striving to build models that generalize reliably to new data. By rigorously separating hyperparameter optimization from model evaluation, it directly addresses the pervasive challenge of overfitting bias in the model development workflow. While computationally demanding, it provides the most trustworthy estimate of a model's true performance on unseen data. For scientists and professionals in critical domains like pharmaceutical development, adopting nested CV is a best practice that ensures predictive models are not just optimized for a specific dataset but are genuinely robust and reliable for informing real-world decisions.

Managing Population Shifts and Ensuring External Validity

In machine learning research, particularly within biomedical and drug development contexts, the phenomena of overfitting and underfitting represent fundamental challenges to model validity. Overfitting occurs when a model learns the training data too closely, including its noise and random fluctuations, resulting in poor performance on new, unseen data [4] [11]. Underfitting, in contrast, happens when a model is too simple to capture the underlying patterns in the data, performing poorly on both training and test sets [4] [11]. Both issues directly impact a model's external validity—the ability to generalize predictions to broader target populations beyond the specific dataset used for training.

Population shifts, where the data distribution in deployment differs from the training data, exacerbate these challenges. In critical domains like healthcare, ensuring that models perform reliably across diverse populations, clinical settings, and time periods is paramount. This technical guide examines methodologies for detecting, assessing, and mitigating the effects of population shifts to enhance the external validity of machine learning models in research and drug development.

Defining the Challenge: Population Shifts and Their Impact on Model Validity

Types of Population Shifts in Biomedical Research

Population shifts in machine learning can be categorized into several types, each posing distinct challenges to external validity. Covariate shift occurs when the distribution of input features changes between training and deployment populations, while the conditional relationship between features and output remains unchanged. Concept shift happens when the very relationship between inputs and outputs changes over time or across populations [107]. In clinical settings, this might manifest as a diagnostic model trained in one demographic group failing in another due to unaccounted biological differences.

The Overfitting-External Validity Connection

Overfitting directly undermines external validity by creating models that appear highly accurate during training and internal validation but fail to maintain this performance in real-world applications. As noted in research on medical AI, "ML models tend to perform better on data from the same cohort than on new data, often due to overfitting, or co-variate shifts" [107]. The high variance characteristic of overfitted models makes them particularly susceptible to performance degradation when faced with population shifts.

Table 1: Characteristics of Model Fit and Impact on External Validity

Model State Training Performance Test Performance Generalization to New Populations Vulnerability to Population Shifts
Underfitting Poor [11] Poor [11] Consistently poor across populations High - cannot capture relevant patterns even without shifts
Proper Fitting Good [4] Good [4] Maintains performance with similar populations Moderate - may degrade with significant distribution changes
Overfitting Excellent [4] [11] Poor [4] [11] Highly variable and unpredictable Very high - memorized patterns fail with slightest shifts

Methodologies for Assessing External Validity

External Validation Protocols

External validation is a necessary practice for properly evaluating medical ML models and assessing their robustness to population shifts [107]. Unlike internal validation methods like cross-validation, external validation tests models on completely separate datasets collected from different cohorts, facilities, or time periods.

A comprehensive external validation framework should assess performance across three dimensions: discrimination (ability to distinguish between classes), calibration (alignment between predicted probabilities and actual outcomes), and utility (clinical usefulness) [107]. This multi-faceted approach provides a more complete picture of how population shifts might impact model performance in real-world scenarios.

Designing Challenging Validation Sets

Rather than using convenience samples for validation, researchers should deliberately curate test sets that include problems of varying difficulty levels representative of real-world challenges [108]. In protein function prediction, for instance, this means including "twilight zone" proteins with low sequence similarity to training examples rather than predominantly easy cases that inflate performance metrics [108].

Table 2: Stratified Validation Framework for Assessing External Validity

Challenge Level Definition Performance Reporting Interpretation
Easy High similarity to training examples Report separately from other levels [108] Tests basic pattern recognition; high performance expected
Moderate Moderate similarity to training examples Report separately from other levels [108] Assesses intermediate generalization capability
Hard Low similarity to training examples (e.g., <30% sequence identity in proteins) [108] Report separately from other levels [108] Tests true generalization to novel cases; most relevant for external validity
Out-of-Distribution From different populations, sites, or time periods Compare with internal performance [107] Directly measures robustness to population shifts

PopulationShiftValidation TrainingData Training Data (Single Population/Site) InternalValidation Internal Validation (Cross-validation/Holdout) TrainingData->InternalValidation ExternalValidation External Validation Datasets InternalValidation->ExternalValidation Dataset1 Similar Population (Same demographics) ExternalValidation->Dataset1 Dataset2 Divergent Population (Different demographics) ExternalValidation->Dataset2 Dataset3 Different Collection Site (Other hospitals/labs) ExternalValidation->Dataset3 Dataset4 Temporal Shift (Data from future period) ExternalValidation->Dataset4 PerformanceAssessment Stratified Performance Assessment Dataset1->PerformanceAssessment Dataset2->PerformanceAssessment Dataset3->PerformanceAssessment Dataset4->PerformanceAssessment EasyCases Easy Cases (High similarity) PerformanceAssessment->EasyCases ModerateCases Moderate Cases (Medium similarity) PerformanceAssessment->ModerateCases HardCases Hard Cases (Low similarity) PerformanceAssessment->HardCases GeneralizationConclusion Generalization Conclusion & External Validity Rating EasyCases->GeneralizationConclusion ModerateCases->GeneralizationConclusion HardCases->GeneralizationConclusion

Diagram 1: External Validation Workflow for Population Shifts

Quantitative Assessment of Dataset Similarity

Beyond performance metrics, assessing the similarity between training and validation datasets is crucial for interpreting external validation results. Methodological approaches include measuring dataset cardinality (size) and dataset similarity using appropriate statistical measures [107]. The Data Agreement Criterion (DAC) and Data Representativeness Criterion (DRC) provide frameworks for evaluating whether external validation datasets are adequate for drawing meaningful conclusions about model robustness [107].

Experimental Protocols for Robust External Validation

Multi-Site Validation Studies

To properly assess external validity, researchers should implement multi-site validation studies that explicitly test models against population shifts:

  • Site Selection: Identify validation sites that differ systematically from training data sources in relevant dimensions (geography, demographics, clinical practices) [107]

  • Protocol Harmonization: Establish standardized data collection and preprocessing protocols across sites while allowing for natural variation in real-world conditions

  • Performance Benchmarking: Compare model performance across sites using consistent metrics, with particular attention to performance degradation patterns

  • Covariate Analysis: Document and analyze differences in feature distributions between training and validation sites to identify specific sources of population shifts

Temporal Validation Protocols

Models can become outdated due to temporal shifts in populations, practices, or disease patterns. Temporal validation assesses model performance on data collected after the training period:

  • Rolling Validation: Train models on historical data and validate on subsequent time periods, repeating as new data becomes available

  • Concept Drift Monitoring: Implement statistical process control methods to detect significant changes in feature distributions or model performance over time

  • Update Triggers: Establish performance degradation thresholds that trigger model retraining or refinement

Mitigation Strategies for Population Shifts

Data-Centric Approaches

MitigationStrategies PopulationShifts Population Shifts Threat to External Validity DataStrategies Data-Centric Strategies PopulationShifts->DataStrategies ModelingStrategies Modeling Strategies PopulationShifts->ModelingStrategies ValidationStrategies Validation Strategies PopulationShifts->ValidationStrategies DiverseTraining Diverse Training Data (Multiple populations/sites) DataStrategies->DiverseTraining DataAugmentation Data Augmentation (Artificial expansion of variation) [63] DataStrategies->DataAugmentation StrategicSampling Strategic Sampling (Oversampling underrepresented groups) DataStrategies->StrategicSampling RobustModel Robust Model With Enhanced External Validity DiverseTraining->RobustModel DataAugmentation->RobustModel StrategicSampling->RobustModel Regularization Regularization Techniques (L1/L2 to prevent overfitting) [4] ModelingStrategies->Regularization EnsembleMethods Ensemble Methods (Combine multiple models) [63] ModelingStrategies->EnsembleMethods DomainAdaptation Domain Adaptation (Explicit adjustment for shifts) ModelingStrategies->DomainAdaptation Regularization->RobustModel EnsembleMethods->RobustModel DomainAdaptation->RobustModel ExternalValidation External Validation (Mandatory for deployment) [107] ValidationStrategies->ExternalValidation ChallengeStratification Challenge Stratification (Easy/Moderate/Hard problems) [108] ValidationStrategies->ChallengeStratification ContinuousMonitoring Continuous Performance Monitoring ValidationStrategies->ContinuousMonitoring ExternalValidation->RobustModel ChallengeStratification->RobustModel ContinuousMonitoring->RobustModel

Diagram 2: Mitigation Strategies for Population Shifts

Improving the diversity and representativeness of training data is fundamental to enhancing external validity:

  • Intentional Sampling: Proactively include underrepresented populations during data collection rather than relying on convenience samples [109]
  • Data Augmentation: Artificially expand training variation using techniques like translation, rotation, and flipping for imaging data, or more sophisticated synthetic data generation methods [63]
  • Multi-Site Training: Incorporate data from multiple collection sites during model development to expose the algorithm to natural variations in populations and practices
Algorithmic Approaches

Several algorithmic strategies can increase model robustness to population shifts:

  • Regularization Techniques: Apply L1 (lasso) or L2 (ridge) regularization to discourage overreliance on specific features and reduce overfitting [4] [11]
  • Domain Adaptation: Implement specialized algorithms that explicitly adjust for differences between source (training) and target (deployment) distributions
  • Invariant Feature Learning: Develop models that learn features invariant across different populations or settings
  • Ensemble Methods: Combine predictions from multiple models trained on different data subsets or with different algorithms to reduce variance and improve generalization [63]
Validation-First Development

Adopt a validation-first approach where external validity considerations guide the entire model development process:

  • Prospective External Validation Planning: Identify potential validation partners and datasets during project initiation rather than after model development

  • Challenge-Centric Evaluation: Curate validation sets specifically around anticipated real-world challenges and population shifts [108]

  • Iterative Refinement: Use external validation results to iteratively improve model robustness rather than as a final gatekeeper

Table 3: Research Reagent Solutions for External Validity Assessment

Tool Category Specific Solutions Function in External Validity Assessment
Validation Frameworks PRECIS-2 tool [109] Categorizes trials along explanatory-pragmatic continuum to enhance generalizability
Statistical Packages Domain adaptation algorithms Explicitly adjusts for distribution shifts between training and deployment populations
Data Collection Tools Multi-site recruitment protocols Facilitates diverse participant enrollment across different demographics and settings
Performance Assessment Challenge-stratified test sets [108] Evaluates model performance across easy, moderate, and hard problems separately
Similarity Metrics Dataset similarity measures [107] Quantifies distributional differences between training and validation datasets
Monitoring Systems Performance dashboards with drift detection Tracks model performance over time and alerts to significant degradation

Managing population shifts and ensuring external validity requires a fundamental shift from model-centric to validation-centric development in machine learning research. By treating overfitting and underfitting not merely as technical challenges but as threats to generalizability, researchers can develop more robust models capable of performing reliably across diverse populations and settings. The methodologies outlined in this guide—comprehensive external validation, challenging assessment protocols, and proactive mitigation strategies—provide a framework for creating machine learning solutions that maintain their predictive power when deployed in the real-world variability of biomedical research and drug development.

Comparative Analysis of Model Performance Across Algorithms

In machine learning research, the ultimate goal is to develop models that generalize effectively, performing reliably on new, unseen data. This pursuit is fundamentally challenged by the twin problems of overfitting and underfitting [4]. Overfitting occurs when a model learns the training data too well, including its noise and irrelevant details, leading to poor performance on test data. In contrast, underfitting happens when a model is too simple to capture the underlying patterns in the data, resulting in suboptimal performance on both training and test sets [11] [110]. The balance between these two extremes is governed by the bias-variance tradeoff, a core concept that highlights the tension between a model's simplicity and its complexity [4]. This paper provides a comparative analysis of model performance across various algorithms, framed within the context of this tradeoff, and offers detailed experimental protocols for robust evaluation, specifically tailored for rigorous academic and industrial research environments.

Theoretical Framework: Overfitting, Underfitting, and the Bias-Variance Tradeoff

Defining Core Concepts

A model's performance and its ability to generalize are intrinsically linked to the errors stemming from bias and variance [4].

  • Underfitting and High Bias: A model with high bias is too simplistic, making strong assumptions about the data and failing to capture its underlying complexities. This leads to underfitting, where the model performs poorly on both training and testing data because it cannot learn the relevant patterns [11] [110]. An example is using a linear regression model to fit data with a quadratic relationship [11].
  • Overfitting and High Variance: A model with high variance is overly complex and flexible. It learns not only the underlying patterns but also the noise and random fluctuations in the training data. This leads to overfitting, characterized by excellent performance on the training data but significantly worse performance on unseen test data [110] [4]. The model essentially memorizes the training data instead of learning to generalize.
The Bias-Variance Tradeoff

The relationship between bias and variance is a tradeoff [4]. Increasing model complexity typically reduces bias but increases variance, raising the risk of overfitting. Conversely, simplifying a model reduces variance but increases bias, raising the risk of underfitting. The objective of model training is to find the optimal balance where both bias and variance are minimized, resulting in a model that generalizes well [11] [4]. The following diagram illustrates this fundamental relationship.

BiasVarianceTradeoff B Underfitting Region A Optimal Model Complexity C Overfitting Region Error Total Error Error->A Bias Bias Error Bias->B Variance Variance Error Variance->C Complexity Model Complexity

Experimental Protocols for Rigorous Model Evaluation

Designing rigorous experiments is paramount for a fair and meaningful comparative analysis. The appropriate methodology depends on whether the research focuses on a domain-specific problem or aims to develop a generic machine learning technique [111].

Protocol for Domain-Specific Model Evaluation

This protocol is used when the goal is to build the best model for a specific, well-defined task (e.g., predicting molecular bioactivity for a specific protein target) [111].

  • Data Collection and Preparation: Assemble a dataset that is representative of the specific application domain. The data must accurately reflect what the model will encounter during inference in a real-world deployment scenario [111].
  • Metric Selection: Choose evaluation metrics that are aligned with the domain's objectives. Common metrics include Accuracy, Precision, Recall, and F1-score for classification, or Mean Absolute Error and R-squared for regression [111].
  • Validation Strategy: Implement a robust validation scheme to estimate real-world performance.
    • Stratified Hold-Out Validation: Split the dataset into training and validation sets (e.g., 80/20), while maintaining the distribution of the target variable in both splits. This is suitable for large datasets [110].
    • K-Fold Cross-Validation: For more robust evaluation, especially with smaller datasets, randomly shuffle the dataset and split it into k folds (typically 5 to 10). Use k-1 folds for training and one fold for validation, repeating the process k times so each fold serves as the validation set once. The final performance is the average across all folds [11] [110].
Protocol for Generic ML Technique Evaluation

This protocol is used when evaluating a new, general-purpose ML technique (e.g., a new activation function or optimizer) that is not tied to a specific domain [111].

  • Diverse Dataset Pool: Curate a pool of datasets that cover diverse data types (images, text, audio) and tasks (classification, regression) to demonstrate the broad applicability of the technique [111].
  • Standardized Metric Calculation: Compute the chosen evaluation metric for each dataset in the pool using a consistent cross-validation strategy (e.g., 5-fold cross-validation) for all models being compared [111].
  • Statistical Testing: To prove that observed superior performance is statistically significant and not due to chance, employ statistical tests. The Wilcoxon signed-rank test is a non-parametric test commonly used to compare two models across multiple datasets [111].

The workflow for selecting and executing the appropriate experimental protocol is summarized below.

ExperimentalProtocol Start Define Research Objective P1 Domain-Specific ML Model Start->P1 P2 Generic ML Technique Start->P2 DS1 Collect Representative Dataset P1->DS1 GEN1 Curate Diverse Dataset Pool P2->GEN1 DS2 Select Domain-Relevant Metric DS1->DS2 DS3 Apply K-Fold Cross-Validation DS2->DS3 End1 Report Performance on Specific Task DS3->End1 GEN2 Compute Metrics for Each Dataset GEN1->GEN2 GEN3 Perform Wilcoxon Signed-Rank Test GEN2->GEN3 End2 Report General Superiority with P-Value GEN3->End2

Quantitative Comparison of Algorithms and Mitigation Techniques

Different algorithm families have inherent tendencies towards bias or variance, which manifest in their performance on training versus test data. The table below summarizes the performance characteristics of common algorithms and standard techniques to address their weaknesses.

Table 1: Algorithm Performance Profile and Mitigation Strategies

Algorithm Family Typical Performance Indicator Common Mitigation Techniques
Linear Models (e.g., Logistic Regression) High bias, prone to underfitting on complex data [11] [4]. Increase model complexity via feature engineering (polynomial features, interaction terms) [11] [4]. Reduce regularization strength [11].
Complex Nonlinear Models (e.g., Deep Neural Networks, Large Decision Trees) High variance, prone to overfitting, especially with limited data [11] [4]. Apply L1/L2 regularization, dropout (for NNs) [11] [4]. Use early stopping [4]. Increase training data size [11] [4].
Ensemble Methods (e.g., Random Forests) Designed to balance bias and variance by aggregating multiple models [11]. Tune number of base estimators and their maximum depth. Use bagging to reduce variance further [11].

The effectiveness of these mitigation strategies can be quantitatively measured by comparing key metrics on training and test data before and after their application. The following table provides a template for such a comparative analysis.

Table 2: Quantitative Framework for Comparing Model Performance Before and After Mitigation

Model Scenario Training Accuracy Test Accuracy Training Loss Test Loss Diagnosis
Deep Neural Network (Baseline) 99.5% 82.0% 0.015 0.75 Severe Overfitting [110]
+ Dropout & Early Stopping 95.5% 94.0% 0.12 0.18 Good Fit
Linear Model (Baseline) 65.0% 63.5% 0.89 0.91 Severe Underfitting [110]
+ Polynomial Features 92.0% 90.5% 0.21 0.23 Good Fit

The Scientist's Toolkit: Essential Research Reagents for ML Experiments

For researchers in fields like drug development, replicating and validating machine learning experiments requires a clear understanding of the core "reagents" and tools. The following table details essential components for a rigorous ML workflow.

Table 3: Essential Research Reagents and Tools for Machine Learning Experiments

Tool / Component Function & Explanation
Stratified Train-Test Split A method for splitting data into training and testing sets while preserving the distribution of the target variable. This prevents skewed performance estimates, especially with imbalanced datasets (e.g., few active compounds vs. many inactive ones) [110].
K-Fold Cross-Validation A robust resampling technique used to obtain a reliable estimate of model performance by training and testing the model k times on different data subsets, mitigating the influence of a single random split [11] [110] [111].
Wilcoxon Signed-Rank Test A non-parametric statistical test used to determine if there is a significant difference between the performance of two models across multiple datasets. It is essential for validating claims about generic ML techniques [111].
Learning Curves Diagnostic plots that show a model's performance (e.g., loss or accuracy) on the training and validation sets over time (epochs) or as a function of training data size. They are critical for identifying overfitting and underfitting [11].
Regularization (L1/L2) A technique that penalizes model complexity by adding a constraint to the loss function. L1 (Lasso) can drive feature coefficients to zero, aiding feature selection, while L2 (Ridge) shrinks all coefficients, producing a more generalizable model [11] [4].

A rigorous comparative analysis of model performance extends beyond simply ranking algorithms by a single accuracy metric. It requires a deep understanding of the bias-variance tradeoff and its manifestations through overfitting and underfitting. As demonstrated, the choice of experimental protocol is critical and must be aligned with the research goal, whether it is to produce a superior domain-specific predictor or a broadly applicable generic technique. By employing robust validation methods like cross-validation, leveraging statistical testing for general claims, and diligently applying mitigation strategies tailored to specific algorithmic weaknesses, researchers and developers can ensure their models are not only powerful but also reliable and generalizable. This disciplined approach is fundamental to building trustworthy machine learning systems for high-stakes fields like drug development.

Integrating Model Evaluation into the MIDD Workflow

Model-Informed Drug Development (MIDD) relies on computational models to inform key drug development decisions, from early discovery through clinical trials and post-market surveillance. The reliability of these decisions hinges entirely on the robustness and predictive performance of the underlying models. Within the broader thesis on overfitting and underfitting in machine learning research, MIDD presents a high-stakes environment where these failure modes can have profound consequences. Overfitting occurs when a model learns not only the underlying signal but also the noise in the training data, resulting in perfect performance on historical data but failure to generalize to new patient populations or experimental conditions [112]. Conversely, underfitting produces models too simplistic to capture essential biological relationships, rendering them useless for prediction even on training data [113].

The paradigm of model evaluation in MIDD has evolved from a simple technical checkpoint to a continuous, comprehensive framework that assesses real-world impact and validation [114]. In 2025, this evolution reflects the understanding that a model's performance on historical data means little if it cannot deliver tangible value while operating responsibly in production environments. Effective evaluation answers three fundamental questions: how well the model performs on unseen data, whether it generalizes across different populations and scenarios, and most critically, whether it is truly ready for deployment in regulatory decision-making [114]. The integration of rigorous, multi-faceted evaluation throughout the MIDD workflow is therefore not merely a technical nicety but a fundamental requirement for mitigating risk and maximizing the return on modeling investments.

Core Model Evaluation Metrics for MIDD

Selecting appropriate evaluation metrics is the cornerstone of robust model assessment in MIDD. The choice of metrics must be guided by the specific problem domain—classification or regression—and the consequences of different types of errors in a pharmaceutical context.

Evaluation Metrics for Classification Tasks

Classification models in MIDD are frequently employed for tasks such as patient stratification, biomarker identification, and adverse event prediction. Their performance is measured using several key metrics, each providing a different perspective on model behavior [59] [30] [115].

Table 1: Key Evaluation Metrics for Classification Models in MIDD

Metric Mathematical Formula MIDD Application Context Interpretation
Accuracy (TP+TN)/(TP+TN+FP+FN) [59] Initial screening for diagnostic models Can be misleading for imbalanced datasets (e.g., rare adverse events) [59] [112]
Precision TP/(TP+FP) [59] Confirming a positive biomarker status; minimizing false leads in drug target identification High precision indicates few false positives [115]
Recall (Sensitivity) TP/(TP+FN) [59] Identifying patients with a rare disease; safety signal detection where missing a true signal is costly High recall indicates few false negatives [59] [115]
F1-Score 2 × (Precision×Recall)/(Precision+Recall) [59] [30] Holistic view when both false positives and false negatives are important Harmonic mean of precision and recall; useful for imbalanced data [30] [115]
AUC-ROC Area under the ROC curve [59] Overall diagnostic performance of a biomarker across all classification thresholds Measures model's ability to distinguish between classes; 0.5 (random) to 1.0 (perfect) [59] [115]
Evaluation Metrics for Regression Tasks

Regression models are central to MIDD applications like predicting pharmacokinetic parameters, drug concentration-time profiles, and clinical response scores. These models are evaluated using error-based metrics [115].

Table 2: Key Evaluation Metrics for Regression Models in MIDD

Metric Mathematical Formula MIDD Application Context Interpretation
Mean Absolute Error (MAE) (1/n) × ∑∣yi − ŷi∣ [115] Predicting PK parameters like clearance or volume of distribution Average error magnitude; robust to outliers [114] [115]
Mean Squared Error (MSE) (1/n) × ∑(yi − ŷi)² [115] Optimizing a dose-exposure model where large errors are unacceptable Penalizes larger errors more heavily than MAE [114] [115]
Root Mean Squared Error (RMSE) √MSE [115] Forecasting clinical trial outcomes Error in original units of the variable; penalizes large errors [115]
R-squared (R²) 1 − (∑(yi − ŷi)² / ∑(yi − ȳ)²) Explaining variability in drug response Proportion of variance in the dependent variable that is predictable from the independent variable(s) [114]
Advanced Probabilistic and Business-Oriented Metrics

Modern MIDD evaluation integrates probabilistic metrics and business-oriented measurements. Probabilistic metrics like Log Loss [59] and Brier Score [114] evaluate the quality of predicted probabilities, which is crucial for risk-based decision making. Business-oriented metrics have also emerged, including expected value frameworks that convert model predictions to monetary value, and cost-sensitive metrics that incorporate the asymmetric costs of different error types based on actual clinical or commercial consequences [114]. For instance, a false negative in a patient stratification model may have a much higher cost than a false positive, a nuance that must be captured in the evaluation.

A Framework for Integrating Evaluation into the MIDD Workflow

Integrating model evaluation is not a single event but a continuous process embedded throughout the MIDD lifecycle. The following workflow diagram illustrates this integration, highlighting key evaluation checkpoints.

midd_evaluation_workflow Start Problem Formulation & Data Collection DataPrep Data Preparation & Feature Engineering Start->DataPrep ModelDev Model Development & Training DataPrep->ModelDev InternalEval Internal Validation (Cross-Validation) ModelDev->InternalEval  Prevent Overfitting & Underfitting InternalEval->ModelDev  Refine Model ExternalEval External Validation (Holdout Test Set) InternalEval->ExternalEval Deployment Model Deployment & Integration ExternalEval->Deployment Monitor Continuous Monitoring & Performance Tracking Deployment->Monitor Retrain Model Retraining & Iteration Monitor->Retrain  If Performance Decays Retrain->DataPrep

Diagram 1: Model Evaluation in the MIDD Workflow. This diagram outlines the continuous integration of evaluation checkpoints to mitigate overfitting and underfitting, ensuring model robustness and reliability.

Foundational Evaluation Techniques

The workflow is supported by concrete methodological approaches.

  • Strict Data Separation: It is essential to maintain a strict separation between training, validation, and test sets to avoid overfitting and ensure unbiased evaluation [59]. The training set is used to train the model, the validation set for tuning hyperparameters, and a final, untouched test set is reserved for the final evaluation before deployment [59] [116].

  • Cross-Validation Techniques: K-fold cross-validation is a standard robust evaluation method where the dataset is partitioned into k folds. The model is trained on k-1 folds and tested on the remaining fold, repeating this process k times [59] [115]. The final performance is averaged across all k trials, which helps reduce overfitting and ensures the model performs well across different data subsets [59]. For imbalanced datasets common in MIDD (e.g., rare event prediction), stratified k-fold cross-validation preserves the percentage of samples for each class in every fold, leading to a more balanced and fair evaluation [59] [112].

Addressing Overfitting and Underfitting in MIDD

The following diagram illustrates the fundamental trade-off between model complexity and error, which is central to diagnosing and addressing overfitting and underfitting.

Diagram 2: The Bias-Variance Trade-Off. Achieving optimal model complexity involves balancing bias (leading to underfitting) and variance (leading to overfitting) to minimize total error [112].

Several best practices can be employed to navigate this trade-off:

  • Combating Overfitting (High Variance): Techniques include regularization (L1, L2) to penalize large weights, early stopping to halt training when validation performance degrades, and pruning for decision trees [112]. Using simpler models or gathering more training data can also be effective.

  • Combating Underfitting (High Bias): Strategies involve using more complex models, feature engineering to create more relevant input variables, and reducing the strength of regularization [112].

Advanced Evaluation: Ensuring Robustness and Fairness in MIDD

Modern model evaluation extends beyond performance metrics to include critical assessments of robustness, fairness, and explainability, which are paramount for regulatory acceptance and ethical deployment.

Fairness and Bias Assessment

ML models can unintentionally perpetuate societal biases if the training data reflects skewed or discriminatory patterns [117]. In MIDD, this could lead to models that perform poorly for specific demographic groups. Evaluation now includes algorithmic bias assessment across multiple dimensions [114]:

  • Group Fairness: Ensuring equal outcomes across different demographic groups (e.g., age, race, gender).
  • Individual Fairness: Guaranteeing similar individuals receive similar predictions. Practical assessment metrics include demographic parity and equalized odds [114].
Robustness, Stability, and Explainability

  • Robustness and Stability: This involves testing model performance under adversarial conditions, including input perturbation analysis and boundary case evaluation [114]. Distribution shift evaluation is increasingly important, involving covariate shift detection (changes in input distribution) and concept drift assessment (changes in relationships between inputs and outputs over time) [114].

  • Explainability and Interpretability: For high-stakes MIDD applications, models must be interpretable. Model-agnostic interpretation methods like SHAP (SHapley Additive exPlanations) and LIME (Local Interpretable Model-agnostic Explanations) help explain individual predictions and overall model behavior, facilitating stakeholder understanding and trust [114].

Experimental Protocol for a Comprehensive MIDD Model Evaluation

This section provides a detailed, actionable protocol for conducting a thorough model evaluation, incorporating the concepts and metrics discussed.

The Scientist's Toolkit: Key Research Reagent Solutions

Table 3: Essential Tools and Materials for MIDD Model Evaluation

Tool/Reagent Function in Evaluation Example/Note
Stratified K-Fold Cross-Validator Partitions data into k folds while preserving class distribution. Critical for imbalanced datasets (e.g., placebo vs. responder) [112] [115].
Hyperparameter Tuning Framework Algorithmically searches for optimal model parameters. Use Bayesian Optimization (e.g., Optuna) for efficiency over Grid Search [112].
Bias Assessment Suite Quantifies model fairness across predefined patient subgroups. Implement metrics for Demographic Parity and Equalized Odds [114].
Model Interpretability Library Explains model predictions and identifies driving features. SHAP or LIME for generating local and global explanations [114].
Holdout Test Set A portion of data completely withheld from model development. Provides final, unbiased performance estimate on "unseen" data [59] [116].
Step-by-Step Evaluation Protocol

Phase 1: Preliminary Setup and Baseline Establishment

  • Data Splitting: Split the dataset into training (70%), validation (15%), and holdout test (15%) sets. Use stratified splitting for classification tasks to maintain class distributions [59] [115]. For time-series PK/PD data, use chronological splits to prevent data leakage [114].
  • Establish Baseline: Compute a simple baseline (e.g., mean response for regression, majority class for classification) to contextualize model performance.

Phase 2: Core Model Validation and Hyperparameter Tuning

  • Internal Validation via Cross-Validation: Perform 5 or 10-fold stratified cross-validation on the training set. This provides a robust estimate of model performance and helps flag overfitting if cross-validation scores are significantly lower than training scores [115].
  • Hyperparameter Tuning: Using the validation set, conduct hyperparameter optimization via Bayesian methods to find the parameter set that maximizes the chosen metric (e.g., F1-score for imbalanced classification) [112].

Phase 3: Comprehensive Performance and Robustness Assessment

  • Final Model Training: Train the final model with the optimized hyperparameters on the combined training and validation dataset.
  • Holdout Test Evaluation: Execute the final evaluation on the untouched holdout test set. Report a suite of metrics (see Tables 1 & 2) to provide a holistic view [59] [114].
  • Bias and Fairness Audit: Use the bias assessment suite to evaluate the model's performance across key demographic subgroups on the holdout set [114].
  • Explainability Analysis: Apply SHAP or LIME to the final model to identify the top features driving predictions and validate their biological or clinical plausibility [114].

Phase 4: Documentation and Reporting

  • Document Results: Compile all results, including metrics from all data splits, feature importance plots, and bias audit findings.
  • Contextualize and Recommend: State the model's readiness for deployment, clearly outlining its limitations, assumptions, and recommended scope of use based on the comprehensive evaluation.

Integrating a rigorous, multi-faceted model evaluation framework directly into the MIDD workflow is a non-negotiable discipline for building trustworthy and impactful models. This guide has outlined a comprehensive approach, from selecting core metrics to implementing advanced checks for fairness and robustness, all framed within the critical context of mitigating overfitting and underfitting. By adopting these practices—treating evaluation not as a final gate but as a continuous, integrative process—researchers and drug development professionals can significantly de-risk their modeling efforts. This leads to more reliable inferences, more confident decision-making, and ultimately, more efficient and successful drug development programs.

Conclusion

Achieving optimal model fit is not merely a technical exercise but a fundamental requirement for developing reliable, regulatory-grade tools in drug development. Success hinges on strategically navigating the bias-variance tradeoff by aligning fit-for-purpose model complexity with specific Questions of Interest and Contexts of Use. The future of MIDD will be shaped by the rigorous application of these principles, coupled with advanced techniques like ensemble learning and robust validation, to manage real-world challenges such as data scarcity and population shifts. Embracing this disciplined approach will accelerate the delivery of safe and effective therapies by increasing model trust, interpretability, and overall impact across the biomedical research pipeline.

References